Minimization of DFA-
| The process of reducing a given DFA to its minimal form is called as minimization of DFA. |
- It contains the minimum number of states.
- The DFA in its minimal form is called as a Minimal DFA.
How To Minimize DFA?
The two popular methods for minimizing a DFA are-
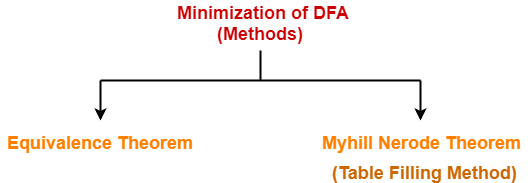
In this article, we will discuss Minimization of DFA Using Equivalence Theorem.
Minimization of DFA Using Equivalence Theorem-
Step-01:
- Eliminate all the dead states and inaccessible states from the given DFA (if any).
Dead State
All those non-final states which transit to itself for all input symbols in ∑ are called as dead states.
Inaccessible State
All those states which can never be reached from the initial state are called as inaccessible states. |
Step-02:
- Draw a state transition table for the given DFA.
- Transition table shows the transition of all states on all input symbols in Σ.
Step-03:
Now, start applying equivalence theorem.
- Take a counter variable k and initialize it with value 0.
- Divide Q (set of states) into two sets such that one set contains all the non-final states and other set contains all the final states.
- This partition is called P0.
Step-04:
- Increment k by 1.
- Find Pk by partitioning the different sets of Pk-1 .
- In each set of Pk-1 , consider all the possible pair of states within each set and if the two states are distinguishable, partition the set into different sets in Pk.
| Two states q1 and q2 are distinguishable in partition Pk for any input symbol ‘a’,
if δ (q1, a) and δ (q2, a) are in different sets in partition Pk-1. |
Step-05:
- Repeat step-04 until no change in partition occurs.
- In other words, when you find Pk = Pk-1, stop.
Step-06:
- All those states which belong to the same set are equivalent.
- The equivalent states are merged to form a single state in the minimal DFA.
|
Number of states in Minimal DFA
= Number of sets in Pk |
PRACTICE PROBLEMS BASED ON MINIMIZATION OF DFA-
Problem-01:
Minimize the given DFA-
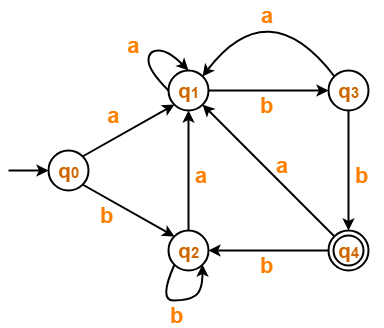
Solution-
Step-01:
The given DFA contains no dead states and inaccessible states.
Step-02:
Draw a state transition table-
| a | b | |
| →q0 | q1 | q2 |
| q1 | q1 | q3 |
| q2 | q1 | q2 |
| q3 | q1 | *q4 |
| *q4 | q1 | q2 |
Step-03:
Now using Equivalence Theorem, we have-
P0 = { q0 , q1 , q2 , q3 } { q4 }
P1 = { q0 , q1 , q2 } { q3 } { q4 }
P2 = { q0 , q2 } { q1 } { q3 } { q4 }
P3 = { q0 , q2 } { q1 } { q3 } { q4 }
Since P3 = P2, so we stop.
From P3, we infer that states q0 and q2 are equivalent and can be merged together.
So, Our minimal DFA is-
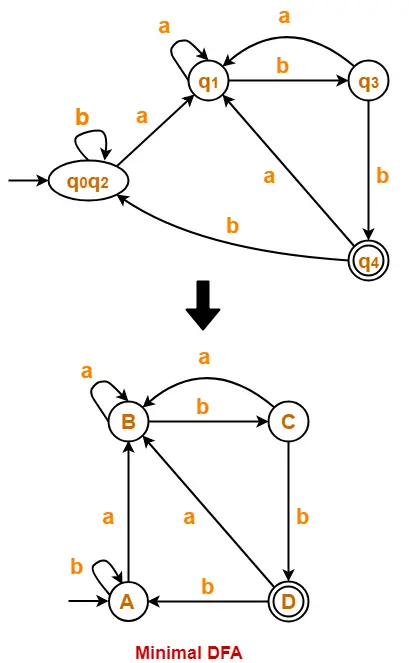
Problem-02:
Minimize the given DFA-
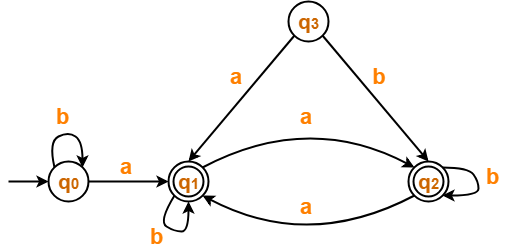
Solution-
Step-01:
- State q3 is inaccessible from the initial state.
- So, we eliminate it and its associated edges from the DFA.
The resulting DFA is-
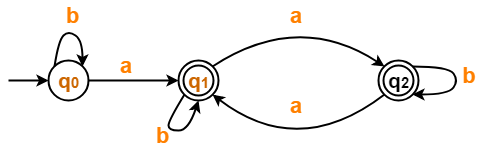
Step-02:
Draw a state transition table-
| a | b | |
| →q0 | *q1 | q0 |
| *q1 | *q2 | *q1 |
| *q2 | *q1 | *q2 |
Step-03:
Now using Equivalence Theorem, we have-
P0 = { q0 } { q1 , q2 }
P1 = { q0 } { q1 , q2 }
Since P1 = P0, so we stop.
From P1, we infer that states q1 and q2 are equivalent and can be merged together.
So, Our minimal DFA is-
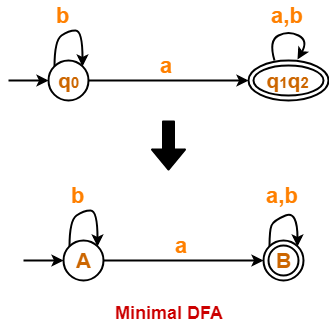
Problem-03:
Minimize the given DFA-
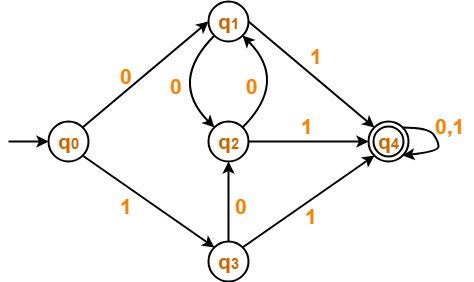
Solution-
Step-01:
The given DFA contains no dead states and inaccessible states.
Step-02:
Draw a state transition table-
| 0 | 1 | |
| →q0 | q1 | q3 |
| q1 | q2 | *q4 |
| q2 | q1 | *q4 |
| q3 | q2 | *q4 |
| *q4 | *q4 | *q4 |
Step-03:
Now using Equivalence Theorem, we have-
P0 = { q0 , q1 , q2 , q3 } { q4 }
P1 = { q0 } { q1 , q2 , q3 } { q4 }
P2 = { q0 } { q1 , q2 , q3 } { q4 }
Since P2 = P1, so we stop.
From P2, we infer that states q1 , q2 and q3 are equivalent and can be merged together.
So, Our minimal DFA is-
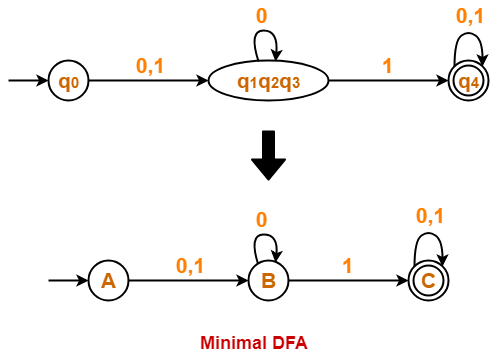
Problem-04:
Minimize the given DFA-
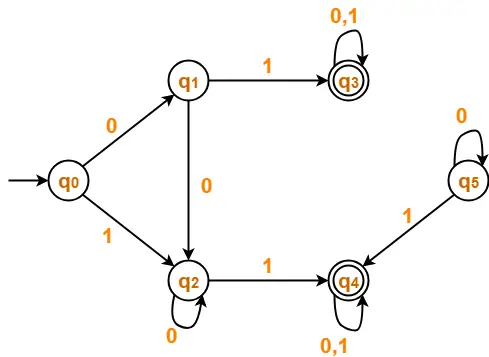
Solution-
Step-01:
- State q5 is inaccessible from the initial state.
- So, we eliminate it and its associated edges from the DFA.
The resulting DFA is-
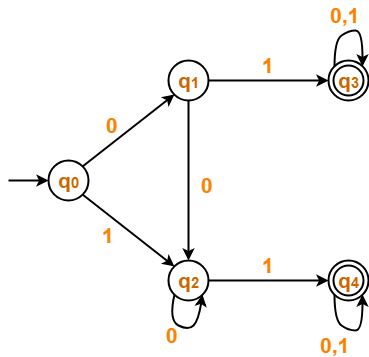
Step-02:
Draw a state transition table-
| 0 | 1 | |
| →q0 | q1 | q2 |
| q1 | q2 | *q3 |
| q2 | q2 | *q4 |
| *q3 | *q3 | *q3 |
| *q4 | *q4 | *q4 |
Step-03:
Now using Equivalence Theorem, we have-
P0 = { q0 , q1 , q2 } { q3 , q4 }
P1 = { q0 } { q1 , q2 } { q3 , q4 }
P2 = { q0 } { q1 , q2 } { q3 , q4 }
Since P2 = P1, so we stop.
From P2, we infer-
- States q1 and q2 are equivalent and can be merged together.
- States q3 and q4 are equivalent and can be merged together.
So, Our minimal DFA is-
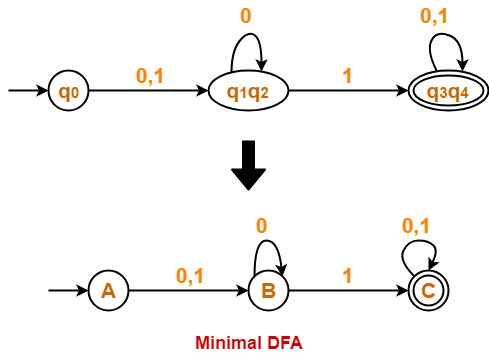
Also Read- Construction of DFA
To gain better understanding about Minimization of DFA,
Next Article- Converting DFA to Regular Expression
Get more notes and other study material of Theory of Automata and Computation.
Watch video lectures by visiting our YouTube channel LearnVidFun.