DFA to Regular Expression | Examples

Theory of Automata & Computation
Spread the love

DFA to Regular Expression-

 

The two popular methods for converting a DFA to its regular expression are-

 

 

  1. Arden’s Method
  2. State Elimination Method

 

In this article, we will discuss State Elimination Method.

 

State Elimination Method-

 

This method involves the following steps in finding the regular expression for any given DFA-

 

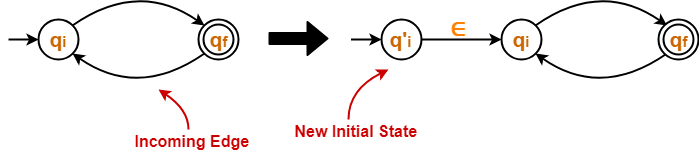
Step-01:

 

Thumb Rule

The initial state of the DFA must not have any incoming edge.

 

  • If there exists any incoming edge to the initial state, then create a new initial state having no incoming edge to it.

 

Example-

 

 

Step-02:

 

Thumb Rule

There must exist only one final state in the DFA.

 

  • If there exists multiple final states in the DFA, then convert all the final states into non-final states and create a new single final state.

 

Example-

 

 

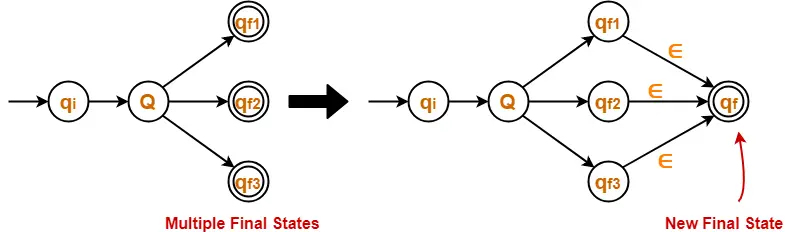
Step-03:

 

Thumb Rule

The final state of the DFA must not have any outgoing edge.

 

  • If there exists any outgoing edge from the final state, then create a new final state having no outgoing edge from it.

 

Example-

 

 

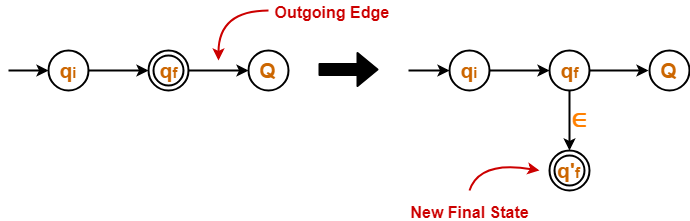
Step-04:

 

  • Eliminate all the intermediate states one by one.
  • These states may be eliminated in any order.

 

In the end,

  • Only an initial state going to the final state will be left.
  • The cost of this transition is the required regular expression.

 

NOTE

The state elimination method can be applied to any finite automata.

(NFA, ∈-NFA, DFA etc)

 

Also Read- Construction of DFA

 

PRACTICE PROBLEMS BASED ON CONVERTING DFA TO REGULAR EXPRESSION-

 

Problem-01:

 

Find regular expression for the following DFA-

 

 

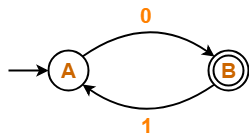
Solution-

 

Step-01:

 

  • Initial state A has an incoming edge.
  • So, we create a new initial state qi.

 

The resulting DFA is-

 

 

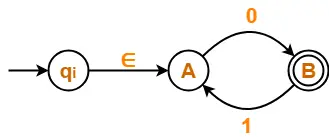
Step-02:

 

  • Final state B has an outgoing edge.
  • So, we create a new final state qf.

 

The resulting DFA is-

 

 

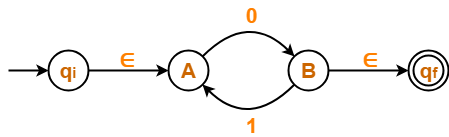
Step-03:

 

Now, we start eliminating the intermediate states.

 

First, let us eliminate state A.

  • There is a path going from state qi to state B via state A.
  • So, after eliminating state A, we put a direct path from state qi to state B having cost ∈.0 = 0
  • There is a loop on state B using state A.
  • So, after eliminating state A, we put a direct loop on state B having cost 1.0 = 10.

 

Eliminating state A, we get-

 

 

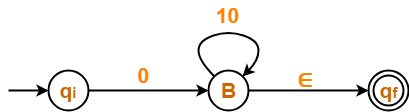
Step-04:

 

Now, let us eliminate state B.

  • There is a path going from state qi to state qf via state B.
  • So, after eliminating state B, we put a direct path from state qi to state qf having cost 0.(10)*.∈ = 0(10)*

 

Eliminating state B, we get-

 

 

From here,

 

Regular Expression = 0(10)*

 

NOTE-

 

In the above question,

  • If we first eliminate state B and then state A, then regular expression would be = (01)*0.
  • This is also the same and correct.

 

Problem-02:

 

Find regular expression for the following DFA-

 

 

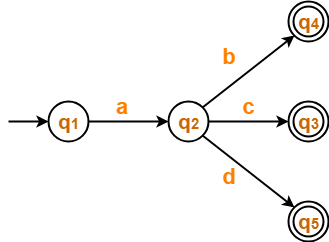
Solution-

 

Step-01:

 

  • There exist multiple final states.
  • So, we convert them into a single final state.

 

The resulting DFA is-

 

 

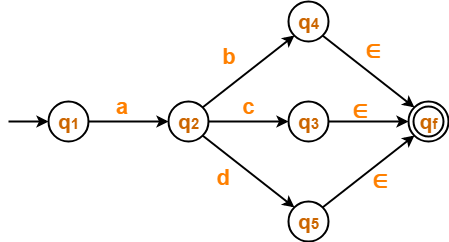
Step-02:

 

Now, we start eliminating the intermediate states.

 

First, let us eliminate state q4.

  • There is a path going from state q2 to state qf via state q4.
  • So, after eliminating state q4 , we put a direct path from state q2 to state qf having cost b.∈ = b.

 

 

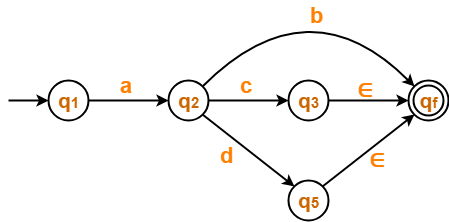
Step-03:

 

Now, let us eliminate state q3.

  • There is a path going from state q2 to state qf via state q3.
  • So, after eliminating state q3 , we put a direct path from state q2 to state qf having cost c.∈ = c.

 

 

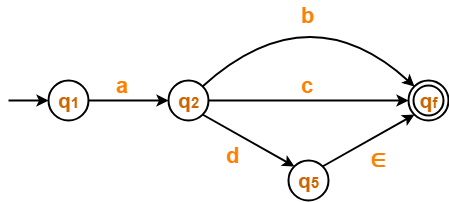
Step-04:

 

Now, let us eliminate state q5.

  • There is a path going from state q2 to state qf via state q5.
  • So, after eliminating state q5 , we put a direct path from state q2 to state qf having cost d.∈ = d.

 

 

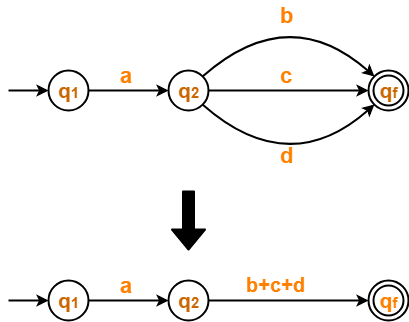
Step-05:

 

Now, let us eliminate state q2.

  • There is a path going from state q1 to state qf via state q2.
  • So, after eliminating state q2 , we put a direct path from state q1 to state qf having cost a.(b+c+d).

 

 

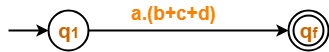
From here,

 

Regular Expression = a(b+c+d)

 

Problem-03:

 

Find regular expression for the following DFA-

 

 

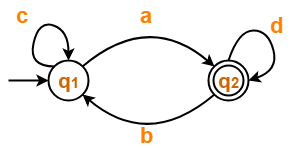
Solution-

 

Step-01:

 

  • Initial state q1 has an incoming edge.
  • So, we create a new initial state qi.

 

The resulting DFA is-

 

 

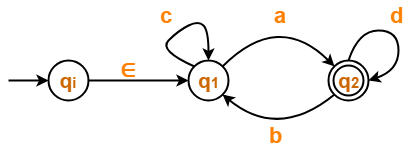
Step-02:

 

  • Final state q2 has an outgoing edge.
  • So, we create a new final state qf.

 

The resulting DFA is-

 

 

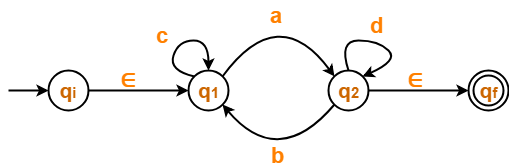
Step-03:

 

Now, we start eliminating the intermediate states.

 

First, let us eliminate state q1.

  • There is a path going from state qi to state q2 via state q1 .
  • So, after eliminating state q1, we put a direct path from state qi to state q2 having cost ∈.c*.a = c*a
  • There is a loop on state q2 using state q1 .
  • So, after eliminating state q1 , we put a direct loop on state q2 having cost b.c*.a = bc*a

 

Eliminating state q1, we get-

 

 

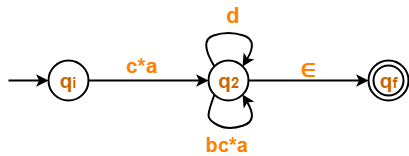
Step-04:

 

Now, let us eliminate state q2.

  • There is a path going from state qi to state qf via state q2 .
  • So, after eliminating state q2, we put a direct path from state qi to state qf having cost c*a(d+bc*a)*∈ = c*a(d+bc*a)*

 

Eliminating state q2, we get-

 

 

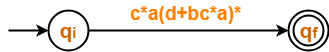
From here,

 

Regular Expression = c*a(d+bc*a)*

 

Problem-04:

 

Find regular expression for the following DFA-

 

 

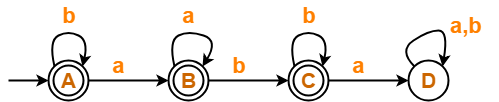
Solution-

 

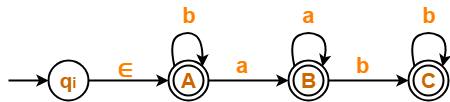
Step-01:

 

  • State D is a dead state as it does not reach to any final state.
  • So, we eliminate state D and its associated edges.

 

The resulting DFA is-

 

 

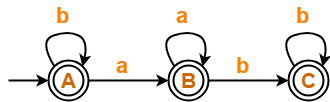
Step-02:

 

  • Initial state A has an incoming edge (self loop).
  • So, we create a new initial state qi.

 

The resulting DFA is-

 

 

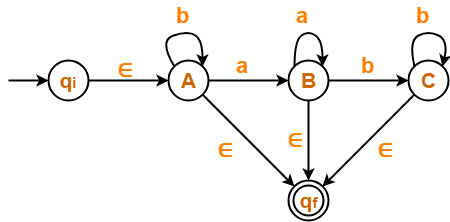
Step-03:

 

  • There exist multiple final states.
  • So, we convert them into a single final state.

 

The resulting DFA is-

 

 

Step-04:

 

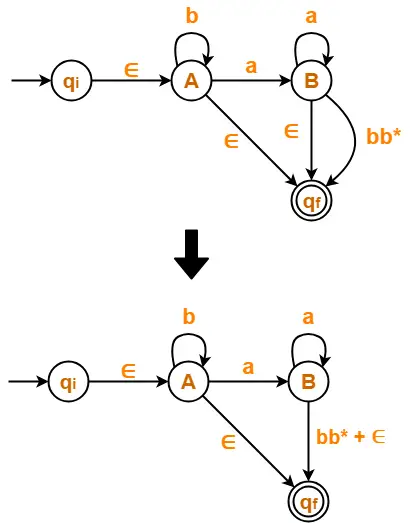
Now, we start eliminating the intermediate states.

 

First, let us eliminate state C.

  • There is a path going from state B to state qf via state C.
  • So, after eliminating state C, we put a direct path from state B to state qf having cost b.b*.∈ = bb*

 

Eliminating state C, we get-

 

 

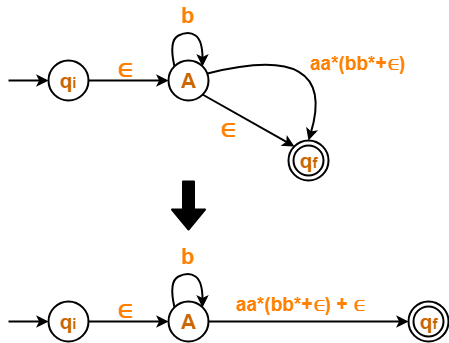
Step-05:

 

Now, let us eliminate state B.

  • There is a path going from state A to state qf via state B.
  • So, after eliminating state B, we put a direct path from state A to state qf having cost a.a*.(bb*+∈) = aa*(bb*+∈)

 

Eliminating state B, we get-

 

 

Step-06:

 

Now, let us eliminate state A.

  • There is a path going from state qi to state qf via state A.
  • So, after eliminating state A, we put a direct path from state qi to state qf having cost ∈.b*.(aa*(bb*+∈)+∈) = b*(aa*(bb*+∈)+∈)

 

Eliminating state A, we get-

 

 

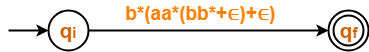
From here,

 

Regular Expression = b*(aa*(bb*+∈)+∈)

 

We know, bb* + ∈ = b*

So, we can also write-

 

Regular Expression = b*(aa*b*+∈)

 

Problem-05:

 

Find regular expression for the following DFA-

 

 

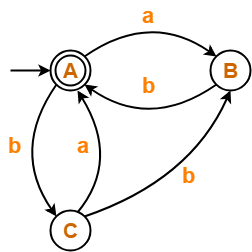
Solution-

 

Step-01:

 

  • Since initial state A has an incoming edge, so we create a new initial state qi.
  • Since final state A has an outgoing edge, so we create a new final state qf.

 

The resulting DFA is-

 

 

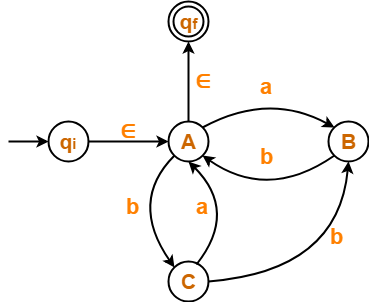
Step-02:

 

Now, we start eliminating the intermediate states.

 

First, let us eliminate state B.

  • There is a path going from state C to state A via state B.
  • So, after eliminating state B, we put a direct path from state C to state A having cost b.b = bb.
  • There is a loop on state A using state B.
  • So, after eliminating state B, we put a direct loop on state A having cost a.b = ab.

 

Eliminating state B, we get-

 

 

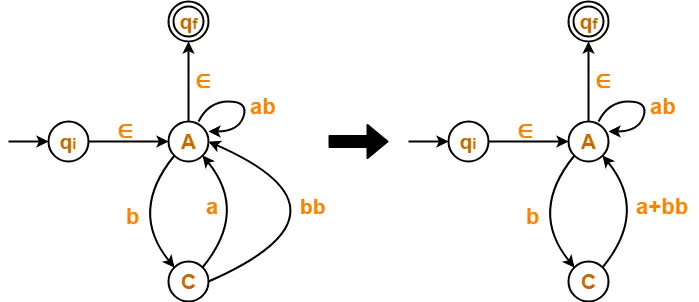
Step-03:

 

Now, let us eliminate state C.

  • There is a loop on state A using state C.
  • So, after eliminating state C, we put a direct loop on state A having cost b.(a+bb) = b(a+bb)

 

Eliminating state C, we get-

 

 

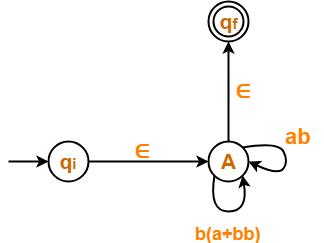
Step-04:

 

Now, let us eliminate state A.

  • There is a path going from state qi to state qf via state A.
  • So, after eliminating state A, we put a direct path from state qi to state qf having cost ∈.(ab + b(a+bb))*∈ = (ab + b(a+bb))*

 

Eliminating state A, we get-

 

 

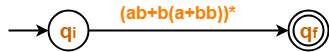
From here,

 

Regular Expression = (ab + b(a+bb))*

 

Problem-06:

 

Find regular expression for the following DFA-

 

 

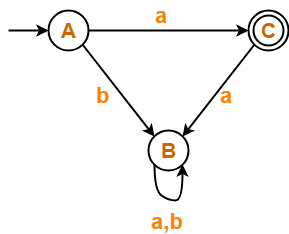
Solution-

 

  • State B is a dead state as it does not reach to the final state.
  • So, we eliminate state B and its associated edges.

 

The resulting DFA is-

 

 

From here,

 

Regular Expression = a

 

Problem-07:

 

Find regular expression for the following DFA-

 

 

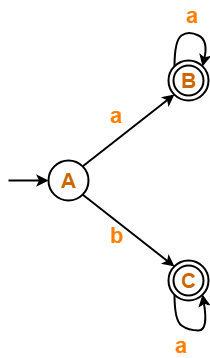
Solution-

 

Step-01:

 

  • There exist multiple final states.
  • So, we create a new single final state.

 

The resulting DFA is-

 

 

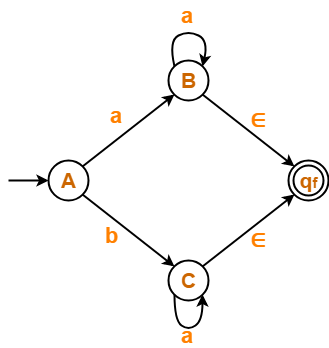
Step-02:

 

Now, we start eliminating the intermediate states.

 

First, let us eliminate state B.

  • There is a path going from state A to state qf via state B.
  • So, after eliminating state B, we put a direct path from state A to state qf having cost a.a*.∈ = aa*.

 

Eliminating state B, we get-

 

 

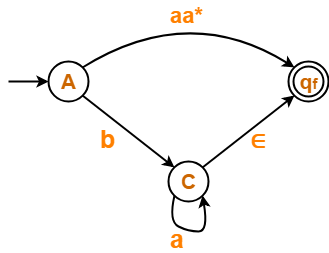
Step-03:

 

Now, let us eliminate state C.

  • There is a path going from state A to state qf via state C.
  • So, after eliminating state C, we put a direct path from state A to state qf having cost b.a*.∈ = ba*.

 

Eliminating state C, we get-

 

 

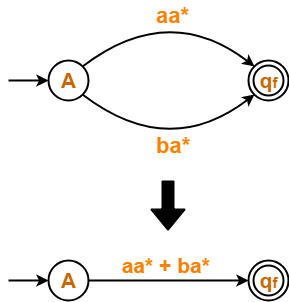
From here,

 

Regular Expression = aa* + ba*

 

Also Read- Minimization of DFA

 

To gain better understanding about Converting DFA to Regular Expression,

Watch this Video Lecture

 

Next Article- Arden’s Theorem

 

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Summary
DFA to Regular Expression | Examples
Article Name
DFA to Regular Expression | Examples
Description
DFA to Regular Expression- The methods to convert DFA to regular expression are- Arden's Method and State Elimination Method. Convert DFA to a Regular Expression Using State Elimination Method. DFA to Regular Expression Conversion Exercises.
Author
Publisher Name
Gate Vidyalay
Publisher Logo

Spread the love