Minimization of DFA | Minimize DFA | Examples

Minimization of DFA-

 

The process of reducing a given DFA to its minimal form is called as minimization of DFA.

 

• It contains the minimum number of states.
• The DFA in its minimal form is called as a Minimal DFA.

 

How To Minimize DFA?

 

The two popular methods for minimizing a DFA are-

 

 

In this article, we will discuss Minimization of DFA Using Equivalence Theorem.

 

Minimization of DFA Using Equivalence Theorem-

 

Step-01:

 

• Eliminate all the dead states and inaccessible states from the given DFA (if any).

 

Dead State   All those non-final states which transit to itself for all input symbols in ∑ are called as dead states.   Inaccessible State   All those states which can never be reached from the initial state are called as inaccessible states.

 

Step-02:

 

• Draw a state transition table for the given DFA.
• Transition table shows the transition of all states on all input symbols in Σ.

 

Step-03:

 

Now, start applying equivalence theorem.

• Take a counter variable k and initialize it with value 0.
• Divide Q (set of states) into two sets such that one set contains all the non-final states and other set contains all the final states.
• This partition is called P₀.

 

Step-04:

 

• Increment k by 1.
• Find P_k by partitioning the different sets of P_k-1 .
• In each set of P_k-1 , consider all the possible pair of states within each set and if the two states are distinguishable, partition the set into different sets in P_k.

 

Two states q1 and q2 are distinguishable in partition Pk for any input symbol ‘a’, if δ (q1, a) and δ (q2, a) are in different sets in partition Pk-1.

 

Step-05:

 

• Repeat step-04 until no change in partition occurs.
• In other words, when you find P_k = P_k-1, stop.

 

Step-06:

 

• All those states which belong to the same set are equivalent.
• The equivalent states are merged to form a single state in the minimal DFA.

 

Number of states in Minimal DFA = Number of sets in Pk

 

PRACTICE PROBLEMS BASED ON MINIMIZATION OF DFA-

 

Problem-01:

 

Minimize the given DFA-

 

 

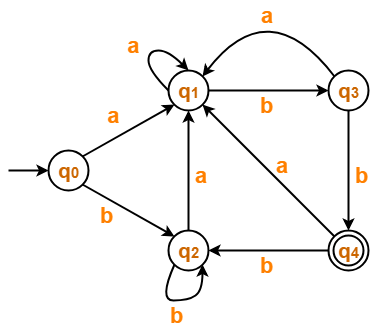
Solution-

 

Step-01:

 

The given DFA contains no dead states and inaccessible states.

 

Step-02:

 

Draw a state transition table-

 

	a	b
→q0	q1	q2
q1	q1	q3
q2	q1	q2
q3	q1	*q4
*q4	q1	q2

 

Step-03:

 

Now using Equivalence Theorem, we have-

P₀ = { q₀ , q₁ , q₂ , q₃ } { q₄ }

P₁ = { q₀ , q₁ , q₂ } { q₃ } { q₄ }

P₂ = { q₀ , q₂ } { q₁ } { q₃ } { q₄ }

P₃ = { q₀ , q₂ } { q₁ } { q₃ } { q₄ }

 

Since P₃ = P₂, so we stop.

From P₃, we infer that states q₀ and q₂ are equivalent and can be merged together.

So, Our minimal DFA is-

 

 

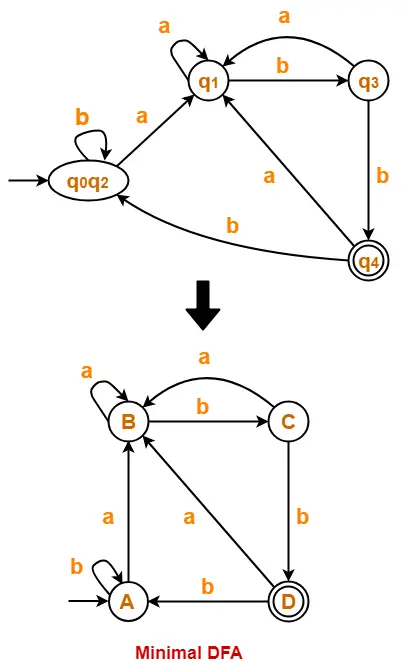
Problem-02:

 

Minimize the given DFA-

 

 

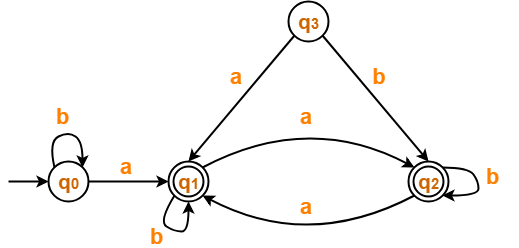
Solution-

 

Step-01:

 

• State q₃ is inaccessible from the initial state.
• So, we eliminate it and its associated edges from the DFA.

 

The resulting DFA is-

 

 

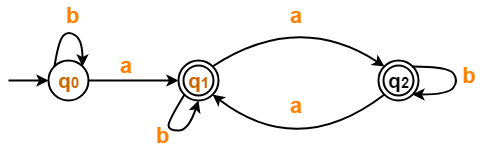
Step-02:

 

Draw a state transition table-

 

	a	b
→q0	*q1	q0
*q1	*q2	*q1
*q2	*q1	*q2

 

Step-03:

 

Now using Equivalence Theorem, we have-

P₀ = { q₀ } { q₁ , q₂ }

P₁ = { q₀ } { q₁ , q₂ }

 

Since P₁ = P₀, so we stop.

From P₁, we infer that states q₁ and q₂ are equivalent and can be merged together.

So, Our minimal DFA is-

 

 

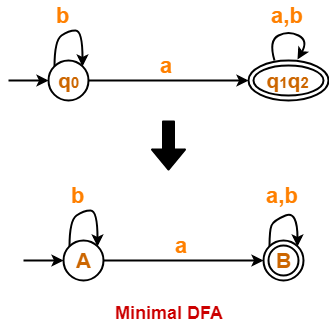
Problem-03:

 

Minimize the given DFA-

 

 

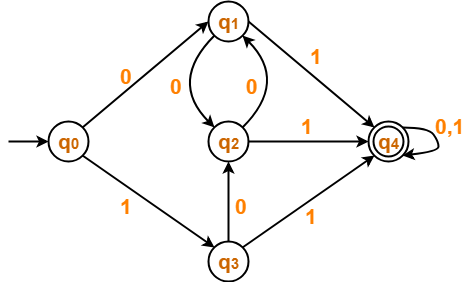
Solution-

 

Step-01:

 

The given DFA contains no dead states and inaccessible states.

 

Step-02:

 

Draw a state transition table-

 

	0	1
→q0	q1	q3
q1	q2	*q4
q2	q1	*q4
q3	q2	*q4
*q4	*q4	*q4

 

Step-03:

 

Now using Equivalence Theorem, we have-

P₀ = { q₀ , q₁ , q₂ , q₃ } { q₄ }

P₁ = { q₀ } { q₁ , q₂ , q₃ } { q₄ }

P₂ = { q₀ } { q₁ , q₂ , q₃ } { q₄ }

 

Since P₂ = P₁, so we stop.

From P₂, we infer that states q₁ , q₂ and q₃ are equivalent and can be merged together.

So, Our minimal DFA is-

 

 

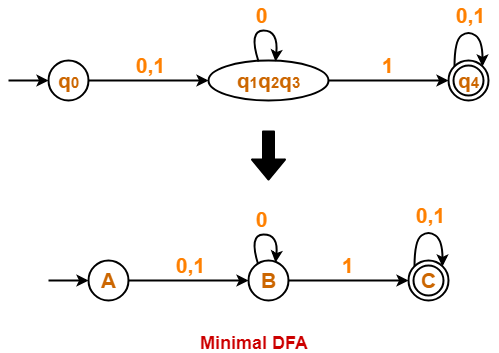
Problem-04:

 

Minimize the given DFA-

 

 

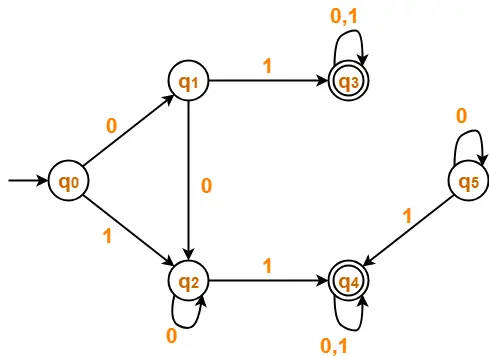
Solution-

 

Step-01:

 

• State q₅ is inaccessible from the initial state.
• So, we eliminate it and its associated edges from the DFA.

 

The resulting DFA is-

 

 

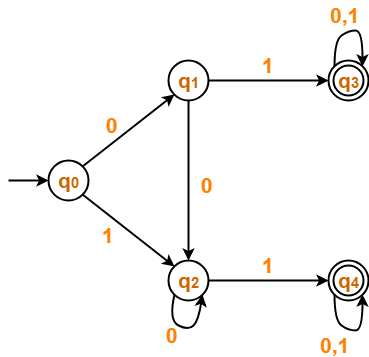
Step-02:

 

Draw a state transition table-

 

	0	1
→q0	q1	q2
q1	q2	*q3
q2	q2	*q4
*q3	*q3	*q3
*q4	*q4	*q4

 

Step-03:

 

Now using Equivalence Theorem, we have-

P₀ = { q₀ , q₁ , q₂ } { q₃ , q₄ }

P₁ = { q₀ } { q₁ , q₂ } { q₃ , q₄ }

P₂ = { q₀ } { q₁ , q₂ } { q₃ , q₄ }

 

Since P₂ = P₁, so we stop.

From P₂, we infer-

• States q₁ and q₂ are equivalent and can be merged together.
• States q₃ and q₄ are equivalent and can be merged together.

So, Our minimal DFA is-

 

 

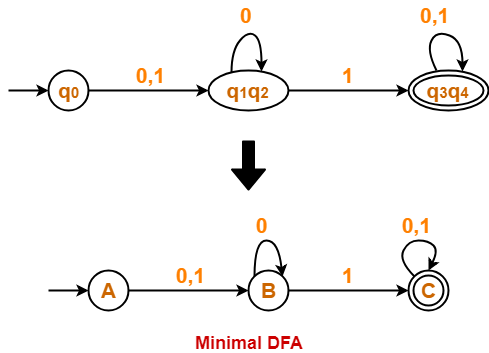
Also Read- Construction of DFA

 

To gain better understanding about Minimization of DFA,

Watch this Video Lecture

 

Next Article- Converting DFA to Regular Expression

 

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.