Prim’s and Kruskal’s Algorithms-
Before you go through this article, make sure that you have gone through the previous articles on Prim’s Algorithm & Kruskal’s Algorithm.
We have discussed-
- Prim’s and Kruskal’s Algorithm are the famous greedy algorithms.
- They are used for finding the Minimum Spanning Tree (MST) of a given graph.
- To apply these algorithms, the given graph must be weighted, connected and undirected.
Some important concepts based on them are-
Concept-01:
If all the edge weights are distinct, then both the algorithms are guaranteed to find the same MST.
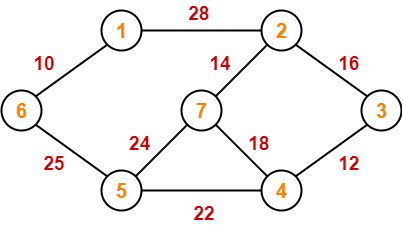
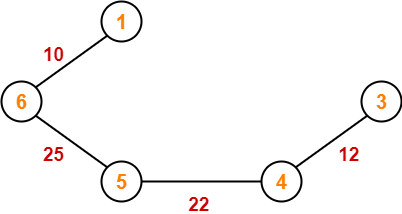
Example-
Consider the following example-
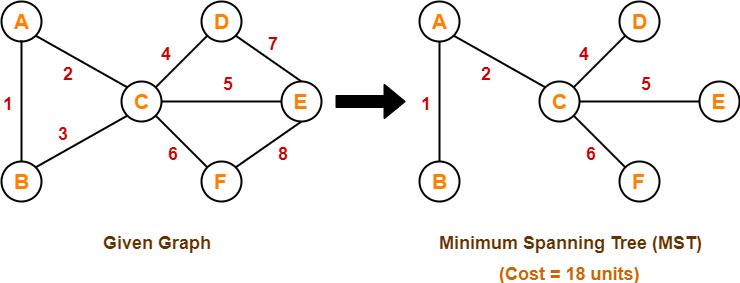
Here, both the algorithms on the above given graph produces the same MST as shown.
Concept-02:
- If all the edge weights are not distinct, then both the algorithms may not always produce the same MST.
- However, cost of both the MSTs would always be same in both the cases.
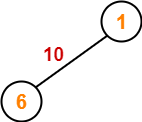
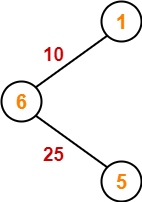
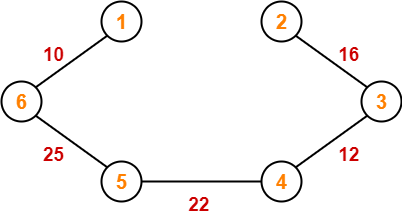
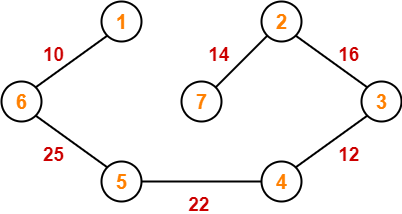
Example-
Consider the following example-
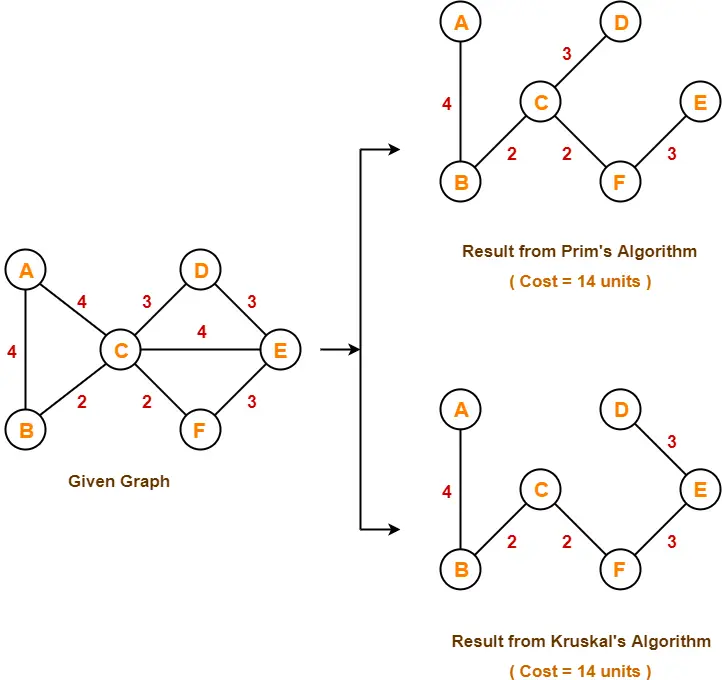
Here, both the algorithms on the above given graph produces different MSTs as shown but the cost is same in both the cases.
Concept-03:
Kruskal’s Algorithm is preferred when-
- The graph is sparse.
- There are less number of edges in the graph like E = O(V)
- The edges are already sorted or can be sorted in linear time.
Prim’s Algorithm is preferred when-
- The graph is dense.
- There are large number of edges in the graph like E = O(V2).
Concept-04:
Difference between Prim’s Algorithm and Kruskal’s Algorithm-
| Prim’s Algorithm | Kruskal’s Algorithm |
| The tree that we are making or growing always remains connected. | The tree that we are making or growing usually remains disconnected. |
| Prim’s Algorithm grows a solution from a random vertex by adding the next cheapest vertex to the existing tree. | Kruskal’s Algorithm grows a solution from the cheapest edge by adding the next cheapest edge to the existing tree / forest. |
| Prim’s Algorithm is faster for dense graphs. | Kruskal’s Algorithm is faster for sparse graphs. |
To gain better understanding about Difference between Prim’s and Kruskal’s Algorithm,
Next Article- Linear Search
Get more notes and other study material of Design and Analysis of Algorithms.
Watch video lectures by visiting our YouTube channel LearnVidFun.