Prim’s Algorithm | Prim’s Algorithm Example | Problems

Prim’s Algorithm-

 

• Prim’s Algorithm is a famous greedy algorithm.
• It is used for finding the Minimum Spanning Tree (MST) of a given graph.
• To apply Prim’s algorithm, the given graph must be weighted, connected and undirected.

 

Prim’s Algorithm Implementation-

 

The implementation of Prim’s Algorithm is explained in the following steps-

 

Step-01:

 

• Randomly choose any vertex.
• The vertex connecting to the edge having least weight is usually selected.

 

Step-02:

 

• Find all the edges that connect the tree to new vertices.
• Find the least weight edge among those edges and include it in the existing tree.
• If including that edge creates a cycle, then reject that edge and look for the next least weight edge.

 

Step-03:

 

• Keep repeating step-02 until all the vertices are included and Minimum Spanning Tree (MST) is obtained.

 

Prim’s Algorithm Time Complexity-

 

Worst case time complexity of Prim’s Algorithm is-

• O(ElogV) using binary heap
• O(E + VlogV) using Fibonacci heap

 

Time Complexity Analysis   If adjacency list is used to represent the graph, then using breadth first search, all the vertices can be traversed in O(V + E) time. We traverse all the vertices of graph using breadth first search and use a min heap for storing the vertices not yet included in the MST. To get the minimum weight edge, we use min heap as a priority queue. Min heap operations like extracting minimum element and decreasing key value takes O(logV) time.   So, overall time complexity = O(E + V) x O(logV) = O((E + V)logV) = O(ElogV)   This time complexity can be improved and reduced to O(E + VlogV) using Fibonacci heap.

 

PRACTICE PROBLEMS BASED ON PRIM’S ALGORITHM-

 

Problem-01:

 

Construct the minimum spanning tree (MST) for the given graph using Prim’s Algorithm-

 

 

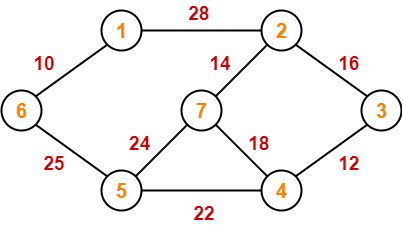
Solution-

 

The above discussed steps are followed to find the minimum cost spanning tree using Prim’s Algorithm-

 

Step-01:

 

 

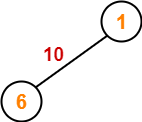
Step-02:

 

 

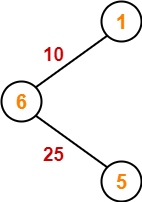
Step-03:

 

 

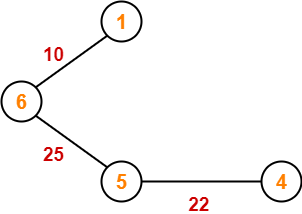
Step-04:

 

 

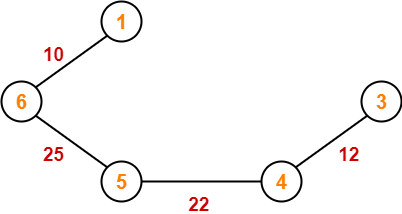
Step-05:

 

 

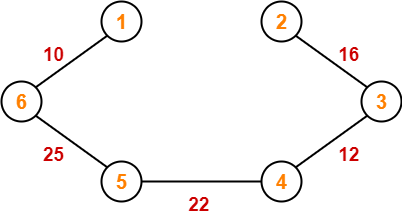
Step-06:

 

 

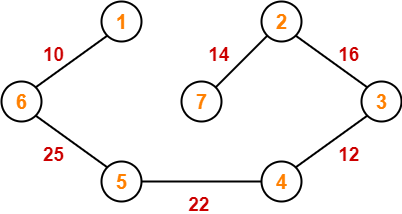
Since all the vertices have been included in the MST, so we stop.

 

Now, Cost of Minimum Spanning Tree

= Sum of all edge weights

= 10 + 25 + 22 + 12 + 16 + 14

= 99 units

 

Problem-02:

 

Using Prim’s Algorithm, find the cost of minimum spanning tree (MST) of the given graph-

 

 

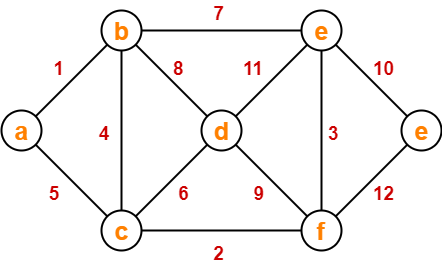
Solution-

 

The minimum spanning tree obtained by the application of Prim’s Algorithm on the given graph is as shown below-

 

 

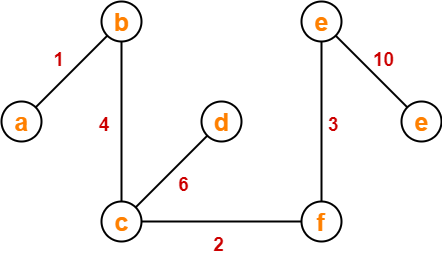
Now, Cost of Minimum Spanning Tree

= Sum of all edge weights

= 1 + 4 + 2 + 6 + 3 + 10

= 26 units

 

To gain better understanding about Prim’s Algorithm,

Watch this Video Lecture

 

To practice previous years GATE problems based on Prim’s Algorithm,

Watch this Video Lecture

 

Next Article- Kruskal’s Algorithm

 

Get more notes and other study material of Design and Analysis of Algorithms.

Watch video lectures by visiting our YouTube channel LearnVidFun.