Kruskal’s Algorithm | Kruskal’s Algorithm Example | Problems

Kruskal’s Algorithm-

 

• Kruskal’s Algorithm is a famous greedy algorithm.
• It is used for finding the Minimum Spanning Tree (MST) of a given graph.
• To apply Kruskal’s algorithm, the given graph must be weighted, connected and undirected.

 

Kruskal’s Algorithm Implementation-

 

The implementation of Kruskal’s Algorithm is explained in the following steps-

 

Step-01:

 

• Sort all the edges from low weight to high weight.

 

Step-02:

 

• Take the edge with the lowest weight and use it to connect the vertices of graph.
• If adding an edge creates a cycle, then reject that edge and go for the next least weight edge.

 

Step-03:

 

• Keep adding edges until all the vertices are connected and a Minimum Spanning Tree (MST) is obtained.

 

Thumb Rule to Remember   The above steps may be reduced to the following thumb rule- Simply draw all the vertices on the paper. Connect these vertices using edges with minimum weights such that no cycle gets formed.

 

Kruskal’s Algorithm Time Complexity-

 

Worst case time complexity of Kruskal’s Algorithm = O(ElogV) or O(ElogE)

 

Analysis-

 

• The edges are maintained as min heap.
• The next edge can be obtained in O(logE) time if graph has E edges.
• Reconstruction of heap takes O(E) time.
• So, Kruskal’s Algorithm takes O(ElogE) time.
• The value of E can be at most O(V²).
• So, O(logV) and O(logE) are same.

 

Special Case-

 

• If the edges are already sorted, then there is no need to construct min heap.
• So, deletion from min heap time is saved.
• In this case, time complexity of Kruskal’s Algorithm = O(E + V)

 

Also Read- Prim’s Algorithm

 

PRACTICE PROBLEMS BASED ON KRUSKAL’S ALGORITHM-

 

Problem-01:

 

Construct the minimum spanning tree (MST) for the given graph using Kruskal’s Algorithm-

 

 

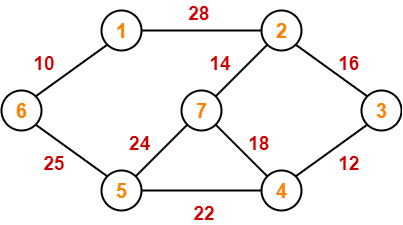
Solution-

 

To construct MST using Kruskal’s Algorithm,

• Simply draw all the vertices on the paper.
• Connect these vertices using edges with minimum weights such that no cycle gets formed.

 

Step-01:

 

 

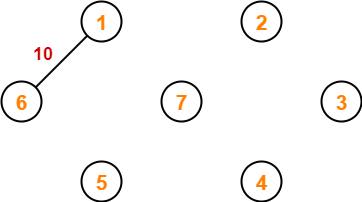
Step-02:

 

 

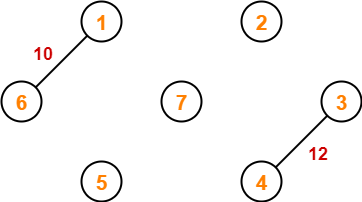
Step-03:

 

 

Step-04:

 

 

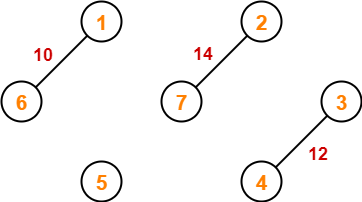
Step-05:

 

 

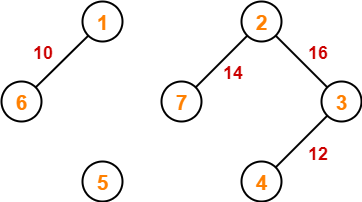
Step-06:

 

 

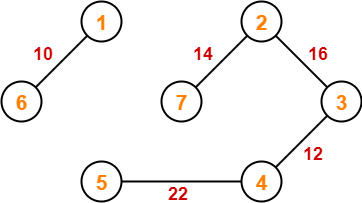
Step-07:

 

 

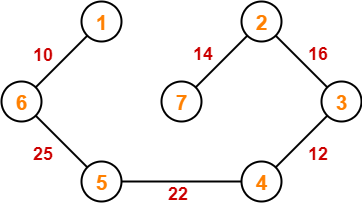
Since all the vertices have been connected / included in the MST, so we stop.

Weight of the  MST

= Sum of all edge weights

= 10 + 25 + 22 + 12 + 16 + 14

= 99 units

 

To gain better understanding about Kruskal’s Algorithm,

Watch this Video Lecture

 

To practice previous years GATE problems based on Kruskal’s Algorithm,

Watch this Video Lecture

 

Next Article- Prim’s Algorithm Vs Kruskal’s Algorithm

 

Get more notes and other study material of Design and Analysis of Algorithms.

Watch video lectures by visiting our YouTube channel LearnVidFun.