Tag: Prim’s Algorithm Pseudocode

Difference Between Prim’s and Kruskal’s Algorithm

Design & Analysis of Algorithms

Prim’s and Kruskal’s Algorithms-

 

Before you go through this article, make sure that you have gone through the previous articles on Prim’s Algorithm & Kruskal’s Algorithm.

 

We have discussed-

  • Prim’s and Kruskal’s Algorithm are the famous greedy algorithms.
  • They are used for finding the Minimum Spanning Tree (MST) of a given graph.
  • To apply these algorithms, the given graph must be weighted, connected and undirected.

 

Some important concepts based on them are-

 

Concept-01:

 

If all the edge weights are distinct, then both the algorithms are guaranteed to find the same MST.

 

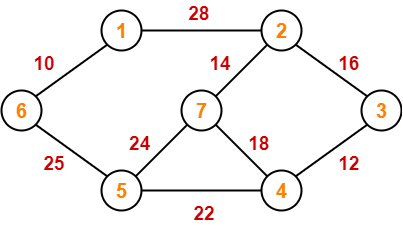
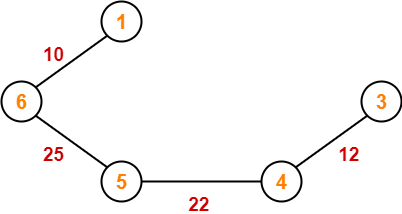
Example-

 

Consider the following example-

 

 

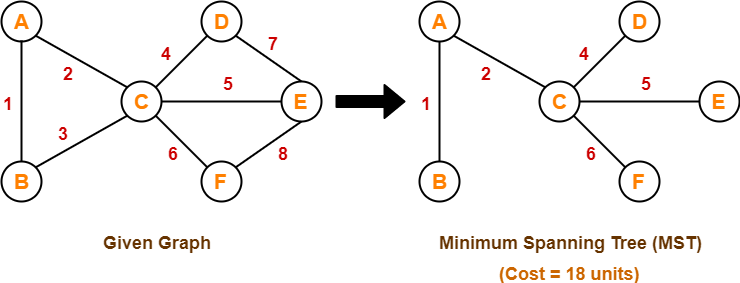
Here, both the algorithms on the above given graph produces the same MST as shown.

 

Concept-02:

 

  • If all the edge weights are not distinct, then both the algorithms may not always produce the same MST.
  • However, cost of both the MSTs would always be same in both the cases.

 

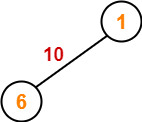
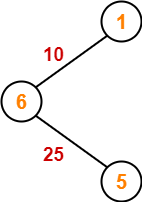
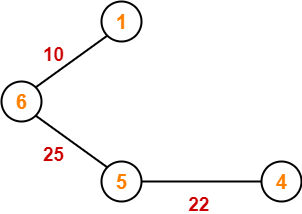
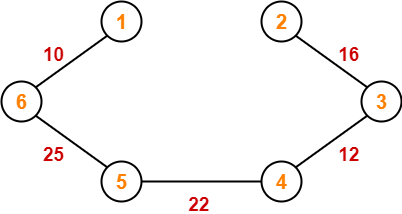
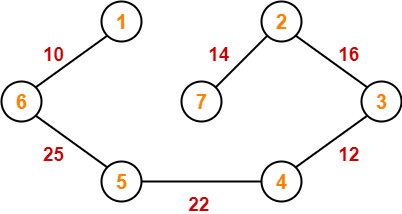
Example-

 

Consider the following example-

 

 

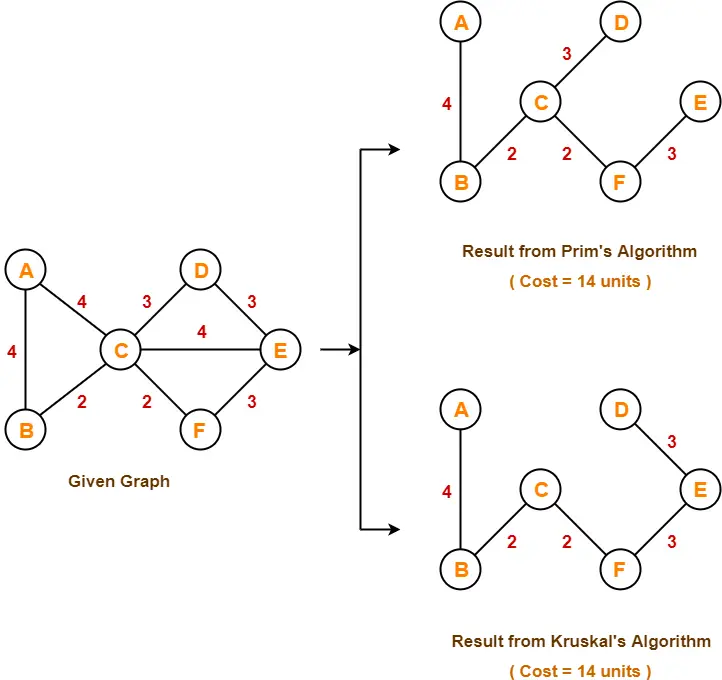
Here, both the algorithms on the above given graph produces different MSTs as shown but the cost is same in both the cases.

 

Concept-03:

 

Kruskal’s Algorithm is preferred when-

  • The graph is sparse.
  • There are less number of edges in the graph like E = O(V)
  • The edges are already sorted or can be sorted in linear time.

 

Prim’s Algorithm is preferred when-

  • The graph is dense.
  • There are large number of edges in the graph like E = O(V2).

 

Concept-04:

 

Difference between Prim’s Algorithm and Kruskal’s Algorithm-

 

Prim’s Algorithm Kruskal’s Algorithm
The tree that we are making or growing always remains connected. The tree that we are making or growing usually remains disconnected.
Prim’s Algorithm grows a solution from a random vertex by adding the next cheapest vertex to the existing tree. Kruskal’s Algorithm grows a solution from the cheapest edge by adding the next cheapest edge to the existing tree / forest.
Prim’s Algorithm is faster for dense graphs. Kruskal’s Algorithm is faster for sparse graphs.

 

To gain better understanding about Difference between Prim’s and Kruskal’s Algorithm,

Watch this Video Lecture

 

Next Article- Linear Search

 

Get more notes and other study material of Design and Analysis of Algorithms.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Prim’s Algorithm | Prim’s Algorithm Example | Problems

Design & Analysis of Algorithms

Prim’s Algorithm-

 

  • Prim’s Algorithm is a famous greedy algorithm.
  • It is used for finding the Minimum Spanning Tree (MST) of a given graph.
  • To apply Prim’s algorithm, the given graph must be weighted, connected and undirected.

 

Prim’s Algorithm Implementation-

 

The implementation of Prim’s Algorithm is explained in the following steps-

 

Step-01:

 

  • Randomly choose any vertex.
  • The vertex connecting to the edge having least weight is usually selected.

 

Step-02:

 

  • Find all the edges that connect the tree to new vertices.
  • Find the least weight edge among those edges and include it in the existing tree.
  • If including that edge creates a cycle, then reject that edge and look for the next least weight edge.

 

Step-03:

 

  • Keep repeating step-02 until all the vertices are included and Minimum Spanning Tree (MST) is obtained.

 

Prim’s Algorithm Time Complexity-

 

Worst case time complexity of Prim’s Algorithm is-

  • O(ElogV) using binary heap
  • O(E + VlogV) using Fibonacci heap

 

Time Complexity Analysis

 

  • If adjacency list is used to represent the graph, then using breadth first search, all the vertices can be traversed in O(V + E) time.
  • We traverse all the vertices of graph using breadth first search and use a min heap for storing the vertices not yet included in the MST.
  • To get the minimum weight edge, we use min heap as a priority queue.
  • Min heap operations like extracting minimum element and decreasing key value takes O(logV) time.

 

So, overall time complexity

= O(E + V) x O(logV)

= O((E + V)logV)

= O(ElogV)

 

This time complexity can be improved and reduced to O(E + VlogV) using Fibonacci heap.

 

PRACTICE PROBLEMS BASED ON PRIM’S ALGORITHM-

 

Problem-01:

 

Construct the minimum spanning tree (MST) for the given graph using Prim’s Algorithm-

 

 

Solution-

 

The above discussed steps are followed to find the minimum cost spanning tree using Prim’s Algorithm-

 

Step-01:

 

 

Step-02:

 

 

Step-03:

 

 

Step-04:

 

 

Step-05:

 

 

Step-06:

 

 

Since all the vertices have been included in the MST, so we stop.

 

Now, Cost of Minimum Spanning Tree

= Sum of all edge weights

= 10 + 25 + 22 + 12 + 16 + 14

= 99 units

 

Problem-02:

 

Using Prim’s Algorithm, find the cost of minimum spanning tree (MST) of the given graph-

 

 

Solution-

 

The minimum spanning tree obtained by the application of Prim’s Algorithm on the given graph is as shown below-

 

 

Now, Cost of Minimum Spanning Tree

= Sum of all edge weights

= 1 + 4 + 2 + 6 + 3 + 10

= 26 units

 

To gain better understanding about Prim’s Algorithm,

Watch this Video Lecture

 

To practice previous years GATE problems based on Prim’s Algorithm,

Watch this Video Lecture

 

Next Article- Kruskal’s Algorithm

 

Get more notes and other study material of Design and Analysis of Algorithms.

Watch video lectures by visiting our YouTube channel LearnVidFun.