3D Transformations in Computer Graphics-
We have discussed-
- Transformation is a process of modifying and re-positioning the existing graphics.
- 3D Transformations take place in a three dimensional plane.
In computer graphics, various transformation techniques are-
In this article, we will discuss about 3D Scaling in Computer Graphics.
3D Scaling in Computer Graphics-
| In computer graphics, scaling is a process of modifying or altering the size of objects. |
- Scaling may be used to increase or reduce the size of object.
- Scaling subjects the coordinate points of the original object to change.
- Scaling factor determines whether the object size is to be increased or reduced.
- If scaling factor > 1, then the object size is increased.
- If scaling factor < 1, then the object size is reduced.
Consider a point object O has to be scaled in a 3D plane.
Let-
- Initial coordinates of the object O = (Xold, Yold,Zold)
- Scaling factor for X-axis = Sx
- Scaling factor for Y-axis = Sy
- Scaling factor for Z-axis = Sz
- New coordinates of the object O after scaling = (Xnew, Ynew, Znew)
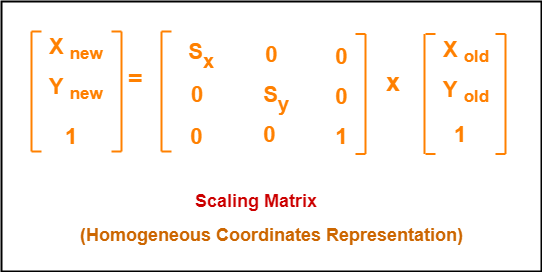
This scaling is achieved by using the following scaling equations-
- Xnew = Xold x Sx
- Ynew = Yold x Sy
- Znew = Zold x Sz
In Matrix form, the above scaling equations may be represented as-

PRACTICE PROBLEMS BASED ON 3D SCALING IN COMPUTER GRAPHICS-
Problem-01:
Given a 3D object with coordinate points A(0, 3, 3), B(3, 3, 6), C(3, 0, 1), D(0, 0, 0). Apply the scaling parameter 2 towards X axis, 3 towards Y axis and 3 towards Z axis and obtain the new coordinates of the object.
Solution-
Given-
- Old coordinates of the object = A (0, 3, 3), B(3, 3, 6), C(3, 0, 1), D(0, 0, 0)
- Scaling factor along X axis = 2
- Scaling factor along Y axis = 3
- Scaling factor along Z axis = 3
For Coordinates A(0, 3, 3)
Let the new coordinates of A after scaling = (Xnew, Ynew, Znew).
Applying the scaling equations, we have-
- Xnew = Xold x Sx = 0 x 2 = 0
- Ynew = Yold x Sy = 3 x 3 = 9
- Znew = Zold x Sz = 3 x 3 = 9
Thus, New coordinates of corner A after scaling = (0, 9, 9).
For Coordinates B(3, 3, 6)
Let the new coordinates of B after scaling = (Xnew, Ynew, Znew).
Applying the scaling equations, we have-
- Xnew = Xold x Sx = 3 x 2 = 6
- Ynew = Yold x Sy = 3 x 3 = 9
- Znew = Zold x Sz = 6 x 3 = 18
Thus, New coordinates of corner B after scaling = (6, 9, 18).
For Coordinates C(3, 0, 1)
Let the new coordinates of C after scaling = (Xnew, Ynew, Znew).
Applying the scaling equations, we have-
- Xnew = Xold x Sx = 3 x 2 = 6
- Ynew = Yold x Sy = 0 x 3 = 0
- Znew = Zold x Sz = 1 x 3 = 3
Thus, New coordinates of corner C after scaling = (6, 0, 3).
For Coordinates D(0, 0, 0)
Let the new coordinates of D after scaling = (Xnew, Ynew, Znew).
Applying the scaling equations, we have-
- Xnew = Xold x Sx = 0 x 2 = 0
- Ynew = Yold x Sy = 0 x 3 = 0
- Znew = Zold x Sz = 0 x 3 = 0
Thus, New coordinates of corner D after scaling = (0, 0, 0).
To gain better understanding about 3D Scaling in Computer Graphics,
Next Article- 3D Reflection in Computer Graphics
Get more notes and other study material of Computer Graphics.
Watch video lectures by visiting our YouTube channel LearnVidFun.