2D Rotation in Computer Graphics | Definition | Examples

2D Transformations in Computer Graphics-

 

We have discussed-

• Transformation is a process of modifying and re-positioning the existing graphics.
• 2D Transformations take place in a two dimensional plane.

 

In computer graphics, various transformation techniques are-

 

 

1. Translation
2. Rotation
3. Scaling
4. Reflection
5. Shear

 

In this article, we will discuss about 2D Rotation in Computer Graphics.

 

2D Rotation in Computer Graphics-

 

In Computer graphics, 2D Rotation is a process of rotating an object with respect to an angle in a two dimensional plane.

 

Consider a point object O has to be rotated from one angle to another in a 2D plane.

 

Let-

• Initial coordinates of the object O = (X_old, Y_old)
• Initial angle of the object O with respect to origin = Φ
• Rotation angle = θ
• New coordinates of the object O after rotation = (X_new, Y_new)

 

 

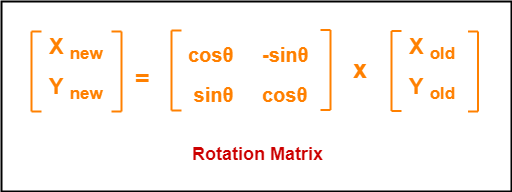
This rotation is achieved by using the following rotation equations-

• X_new = X_old x cosθ – Y_old x sinθ
• Y_new = X_old x sinθ + Y_old x cosθ

 

In Matrix form, the above rotation equations may be represented as-

 

 

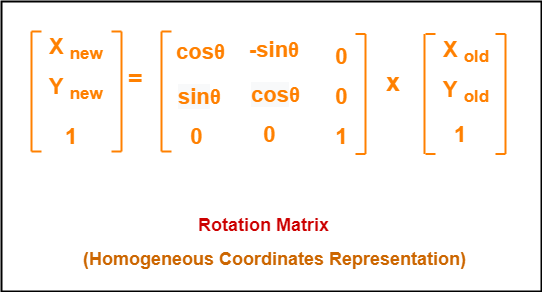
For homogeneous coordinates, the above rotation matrix may be represented as a 3 x 3 matrix as-

 

 

PRACTICE PROBLEMS BASED ON 2D ROTATION IN COMPUTER GRAPHICS-

 

Problem-01:

 

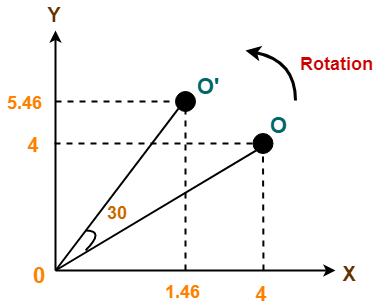
Given a line segment with starting point as (0, 0) and ending point as (4, 4). Apply 30 degree rotation anticlockwise direction on the line segment and find out the new coordinates of the line.

 

Solution-

 

We rotate a straight line by its end points with the same angle. Then, we re-draw a line between the new end points.

 

Given-

• Old ending coordinates of the line = (X_old, Y_old) = (4, 4)
• Rotation angle = θ = 30º

 

Let new ending coordinates of the line after rotation = (X_new, Y_new).

 

Applying the rotation equations, we have-

 

X_new

= X_old x cosθ – Y_old x sinθ

= 4 x cos30º – 4 x sin30º

= 4 x (√3 / 2) – 4 x (1 / 2)

= 2√3 – 2

= 2(√3 – 1)

= 2(1.73 – 1)

= 1.46

 

Y_new

= X_old x sinθ + Y_old x cosθ

= 4 x sin30º + 4 x cos30º

= 4 x (1 / 2) + 4 x (√3 / 2)

= 2 + 2√3

= 2(1 + √3)

= 2(1 + 1.73)

= 5.46

 

Thus, New ending coordinates of the line after rotation = (1.46, 5.46).

 

Alternatively,

 

In matrix form, the new ending coordinates of the line after rotation may be obtained as-

 

 

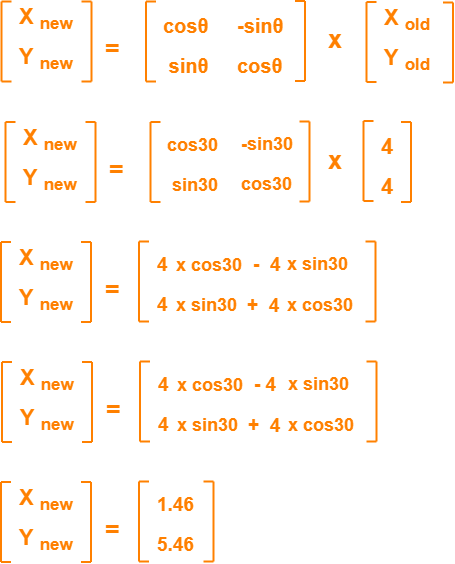
Thus, New ending coordinates of the line after rotation = (1.46, 5.46).

 

 

Problem-02:

 

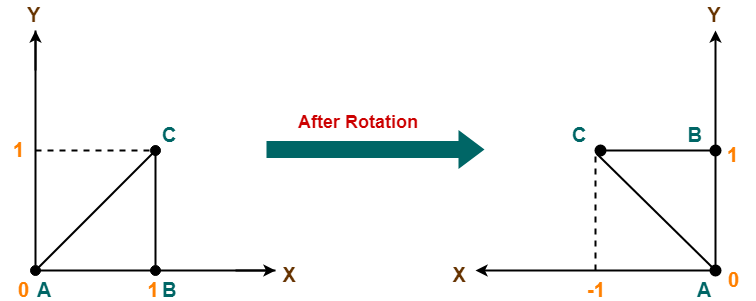
Given a triangle with corner coordinates (0, 0), (1, 0) and (1, 1). Rotate the triangle by 90 degree anticlockwise direction and find out the new coordinates.

 

Solution-

 

We rotate a polygon by rotating each vertex of it with the same rotation angle.

 

Given-

• Old corner coordinates of the triangle = A (0, 0), B(1, 0), C(1, 1)
• Rotation angle = θ = 90º

 

For Coordinates A(0, 0)

 

Let the new coordinates of corner A after rotation = (X_new, Y_new).

 

Applying the rotation equations, we have-

 

X_new

= X_old x cosθ – Y_old x sinθ

= 0 x cos90º – 0 x sin90º

= 0

 

Y_new

= X_old x sinθ + Y_old x cosθ

= 0 x sin90º + 0 x cos90º

= 0

 

Thus, New coordinates of corner A after rotation = (0, 0).

 

For Coordinates B(1, 0)

 

Let the new coordinates of corner B after rotation = (X_new, Y_new).

 

X_new

= X_old x cosθ – Y_old x sinθ

= 1 x cos90º – 0 x sin90º

= 0

 

Y_new

= X_old x sinθ + Y_old x cosθ

= 1 x sin90º + 0 x cos90º

= 1 + 0

= 1

 

Thus, New coordinates of corner B after rotation = (0, 1).

 

For Coordinates C(1, 1)

 

Let the new coordinates of corner C after rotation = (X_new, Y_new).

 

X_new

= X_old x cosθ – Y_old x sinθ

= 1 x cos90º – 1 x sin90º

= 0 – 1

= -1

 

Y_new

= X_old x sinθ + Y_old x cosθ

= 1 x sin90º + 1 x cos90º

= 1 + 0

= 1

 

Thus, New coordinates of corner C after rotation = (-1, 1).

 

Thus, New coordinates of the triangle after rotation = A (0, 0), B(0, 1), C(-1, 1).

 

 

To gain better understanding about 2D Rotation in Computer Graphics,

Watch this Video Lecture

 

Next Article- 2D Scaling in Computer Graphics

 

Get more notes and other study material of Computer Graphics.

Watch video lectures by visiting our YouTube channel LearnVidFun.