3D Reflection in Computer Graphics | Definition | Examples

3D Transformations in Computer Graphics-

 

We have discussed-

• Transformation is a process of modifying and re-positioning the existing graphics.
• 3D Transformations take place in a three dimensional plane.

 

In computer graphics, various transformation techniques are-

 

 

1. Translation
2. Rotation
3. Scaling
4. Reflection
5. Shear

 

In this article, we will discuss about 3D Reflection in Computer Graphics.

 

3D Reflection in Computer Graphics-

 

• Reflection is a kind of rotation where the angle of rotation is 180 degree.
• The reflected object is always formed on the other side of mirror.
• The size of reflected object is same as the size of original object.

 

Consider a point object O has to be reflected in a 3D plane.

 

Let-

• Initial coordinates of the object O = (X_old, Y_old, Z_old)
• New coordinates of the reflected object O after reflection = (X_new, Y_new,Z_new)

 

In 3 dimensions, there are 3 possible types of reflection-

 

 

• Reflection relative to XY plane
• Reflection relative to YZ plane
• Reflection relative to XZ plane

 

Reflection Relative to XY Plane:

 

This reflection is achieved by using the following reflection equations-

• X_new = X_old
• Y_new = Y_old
• Z_new = -Z_old

 

In Matrix form, the above reflection equations may be represented as-

 

 

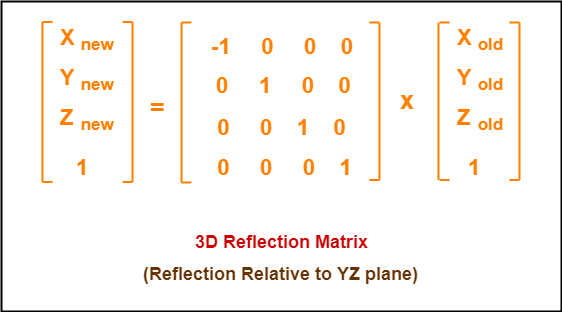
Reflection Relative to YZ Plane:

 

This reflection is achieved by using the following reflection equations-

• X_new = -X_old
• Y_new = Y_old
• Z_new = Z_old

 

In Matrix form, the above reflection equations may be represented as-

 

 

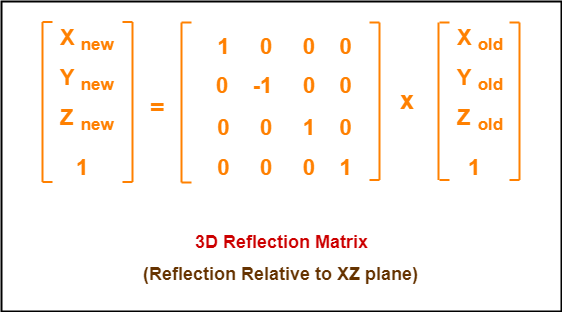
Reflection Relative to XZ Plane:

 

This reflection is achieved by using the following reflection equations-

• X_new = X_old
• Y_new = -Y_old
• Z_new = Z_old

 

In Matrix form, the above reflection equations may be represented as-

 

 

PRACTICE PROBLEMS BASED ON 3D REFLECTION IN COMPUTER GRAPHICS-

 

Problem-01:

 

Given a 3D triangle with coordinate points A(3, 4, 1), B(6, 4, 2), C(5, 6, 3). Apply the reflection on the XY plane and find out the new coordinates of the object.

 

Solution-

 

Given-

• Old corner coordinates of the triangle = A (3, 4, 1), B(6, 4, 2), C(5, 6, 3)
• Reflection has to be taken on the XY plane

 

For Coordinates A(3, 4, 1)

 

Let the new coordinates of corner A after reflection = (X_new, Y_new, Z_new).

 

Applying the reflection equations, we have-

• X_new = X_old = 3
• Y_new = Y_old = 4
• Z_new = -Z_old = -1

 

Thus, New coordinates of corner A after reflection = (3, 4, -1).

 

For Coordinates B(6, 4, 2)

 

Let the new coordinates of corner B after reflection = (X_new, Y_new, Z_new).

 

Applying the reflection equations, we have-

• X_new = X_old = 6
• Y_new = Y_old = 4
• Z_new = -Z_old = -2

 

Thus, New coordinates of corner B after reflection = (6, 4, -2).

 

For Coordinates C(5, 6, 3)

 

Let the new coordinates of corner C after reflection = (X_new, Y_new, Z_new).

 

Applying the reflection equations, we have-

• X_new = X_old = 5
• Y_new = Y_old = 6
• Z_new = -Z_old = -3

 

Thus, New coordinates of corner C after reflection = (5, 6, -3).

Thus, New coordinates of the triangle after reflection = A (3, 4, -1), B(6, 4, -2), C(5, 6, -3).

 

Problem-02:

 

Given a 3D triangle with coordinate points A(3, 4, 1), B(6, 4, 2), C(5, 6, 3). Apply the reflection on the XZ plane and find out the new coordinates of the object.

 

Solution-

 

Given-

• Old corner coordinates of the triangle = A (3, 4, 1), B(6, 4, 2), C(5, 6, 3)
• Reflection has to be taken on the XZ plane

 

For Coordinates A(3, 4, 1)

 

Let the new coordinates of corner A after reflection = (X_new, Y_new, Z_new).

 

Applying the reflection equations, we have-

• X_new = X_old = 3
• Y_new = -Y_old = -4
• Z_new = Z_old = 1

 

Thus, New coordinates of corner A after reflection = (3, -4, 1).

 

For Coordinates B(6, 4, 2)

 

Let the new coordinates of corner B after reflection = (X_new, Y_new, Z_new).

 

Applying the reflection equations, we have-

• X_new = X_old = 6
• Y_new = -Y_old = -4
• Z_new = Z_old = 2

 

Thus, New coordinates of corner B after reflection = (6, -4, 2).

 

For Coordinates C(5, 6, 3)

 

Let the new coordinates of corner C after reflection = (X_new, Y_new, Z_new).

 

Applying the reflection equations, we have-

• X_new = X_old = 5
• Y_new = -Y_old = -6
• Z_new = Z_old = 3

 

Thus, New coordinates of corner C after reflection = (5, -6, 3).

Thus, New coordinates of the triangle after reflection = A (3, -4, 1), B(6, -4, 2), C(5, -6, 3).

 

To gain better understanding about 3D Reflection in Computer Graphics,

Watch this Video Lecture

 

Next Article- 3D Shearing in Computer Graphics

 

Get more notes and other study material of Computer Graphics.

Watch video lectures by visiting our YouTube channel LearnVidFun.