Tree Data Structure-
Before you go through this article, make sure that you have gone through the previous article on Tree Data Structure.
We have discussed-
- Tree is a non-linear data structure.
- In a tree data structure, a node can have any number of child nodes.
In this article, we will discuss about Binary Trees.
Binary Tree-
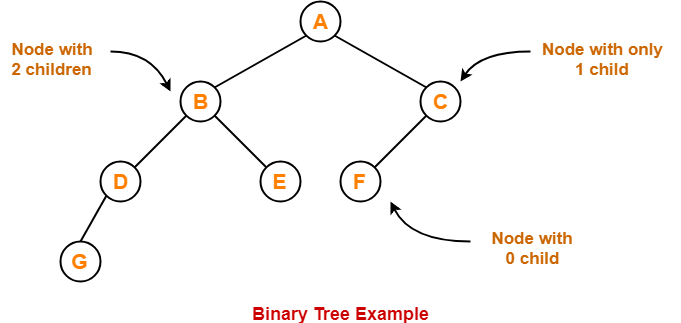
| Binary tree is a special tree data structure in which each node can have at most 2 children.
Thus, in a binary tree, Each node has either 0 child or 1 child or 2 children. |
Example-
Unlabeled Binary Tree-
| A binary tree is unlabeled if its nodes are not assigned any label. |
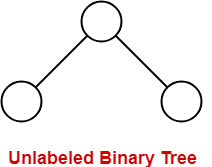

Example-
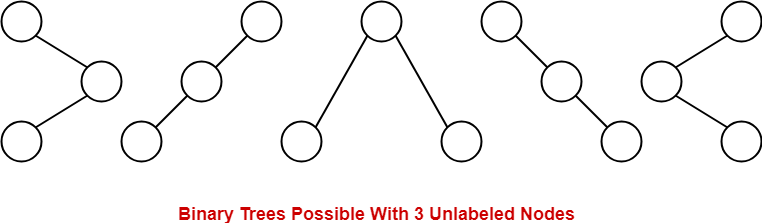
Consider we want to draw all the binary trees possible with 3 unlabeled nodes.
Using the above formula, we have-
Number of binary trees possible with 3 unlabeled nodes
= 2 x 3C3 / (3 + 1)
= 6C3 / 4
= 5
Thus,
- With 3 unlabeled nodes, 5 unlabeled binary trees are possible.
- These unlabeled binary trees are as follows-
Labeled Binary Tree-
| A binary tree is labeled if all its nodes are assigned a label. |
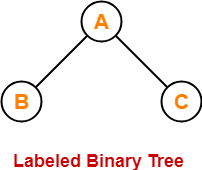

Example-
Consider we want to draw all the binary trees possible with 3 labeled nodes.
Using the above formula, we have-
Number of binary trees possible with 3 labeled nodes
= { 2 x 3C3 / (3 + 1) } x 3!
= { 6C3 / 4 } x 6
= 5 x 6
= 30
Thus,
- With 3 labeled nodes, 30 labeled binary trees are possible.
- Each unlabeled structure gives rise to 3! = 6 different labeled structures.
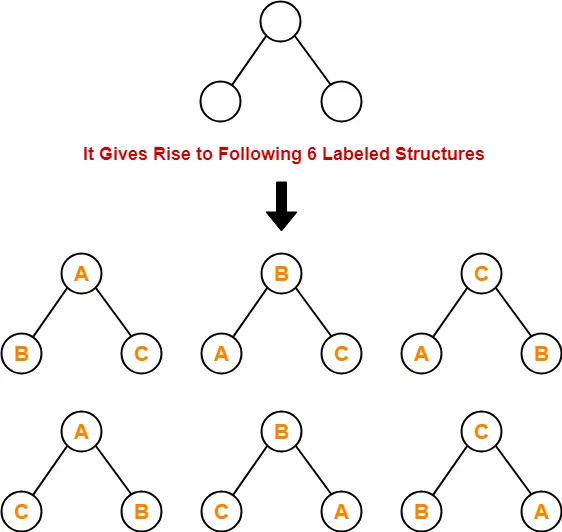
Similarly,
- Every other unlabeled structure gives rise to 6 different labeled structures.
- Thus, in total 30 different labeled binary trees are possible.
Types of Binary Trees-
Binary trees can be of the following types-
- Rooted Binary Tree
- Full / Strictly Binary Tree
- Complete / Perfect Binary Tree
- Almost Complete Binary Tree
- Skewed Binary Tree
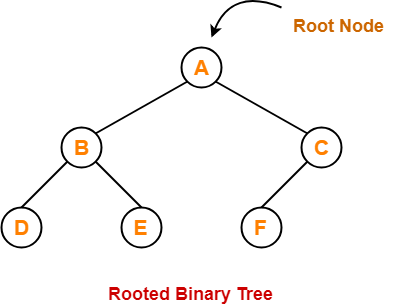
1. Rooted Binary Tree-
A rooted binary tree is a binary tree that satisfies the following 2 properties-
- It has a root node.
- Each node has at most 2 children.
Example-
2. Full / Strictly Binary Tree-
- A binary tree in which every node has either 0 or 2 children is called as a Full binary tree.
- Full binary tree is also called as Strictly binary tree.
Example-
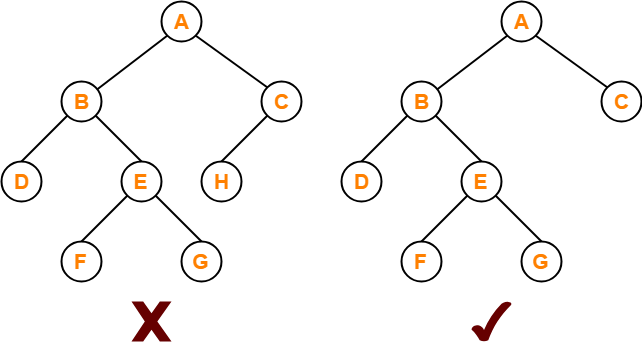
Here,
- First binary tree is not a full binary tree.
- This is because node C has only 1 child.
3. Complete / Perfect Binary Tree-
A complete binary tree is a binary tree that satisfies the following 2 properties-
- Every internal node has exactly 2 children.
- All the leaf nodes are at the same level.
Complete binary tree is also called as Perfect binary tree.
Example-
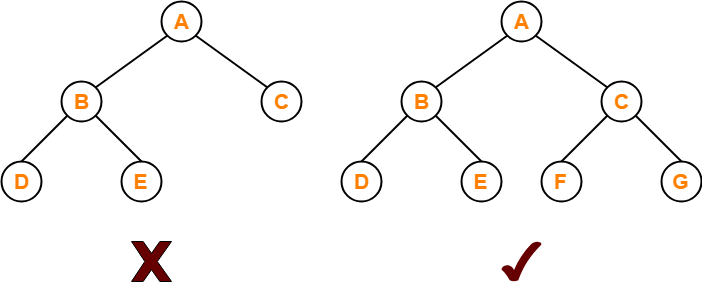
Here,
- First binary tree is not a complete binary tree.
- This is because all the leaf nodes are not at the same level.
4. Almost Complete Binary Tree-
An almost complete binary tree is a binary tree that satisfies the following 2 properties-
- All the levels are completely filled except possibly the last level.
- The last level must be strictly filled from left to right.
Example-
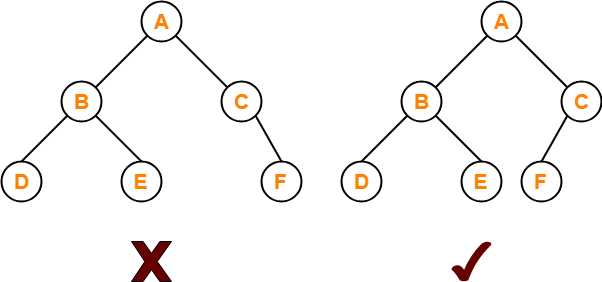
Here,
- First binary tree is not an almost complete binary tree.
- This is because the last level is not filled from left to right.
5. Skewed Binary Tree-
A skewed binary tree is a binary tree that satisfies the following 2 properties-
- All the nodes except one node has one and only one child.
- The remaining node has no child.
OR
A skewed binary tree is a binary tree of n nodes such that its depth is (n-1).
Example-
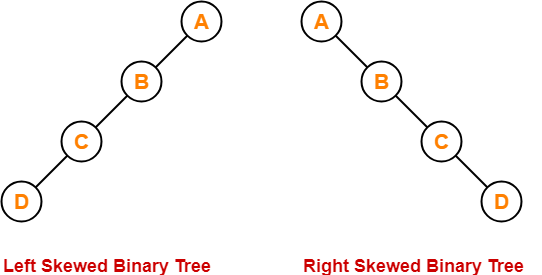
To gain better understanding about Binary Tree and its types-
Also Read- Binary Tree Traversal
Download Handwritten Notes Here-
Next Article- Binary Tree Properties
Get more notes and other study material of Data Structures.
Watch video lectures by visiting our YouTube channel LearnVidFun.
