Syntax Trees-
| Syntax trees are abstract or compact representation of parse trees.
They are also called as Abstract Syntax Trees. |
Example-
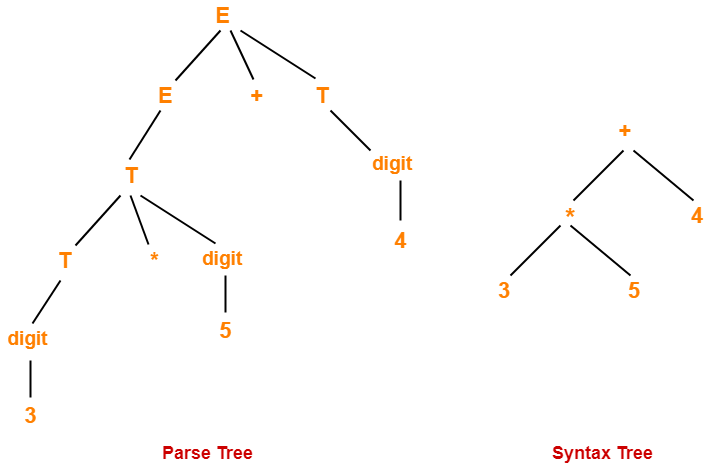
Also Read- Parse Trees
Parse Trees Vs Syntax Trees-
| Parse Tree | Syntax Tree |
| Parse tree is a graphical representation of the replacement process in a derivation. | Syntax tree is the compact form of a parse tree. |
| Each interior node represents a grammar rule.
Each leaf node represents a terminal. |
Each interior node represents an operator.
Each leaf node represents an operand. |
| Parse trees provide every characteristic information from the real syntax. | Syntax trees do not provide every characteristic information from the real syntax. |
| Parse trees are comparatively less dense than syntax trees. | Syntax trees are comparatively more dense than parse trees. |
NOTE-
Syntax trees are called as Abstract Syntax Trees because-
- They are abstract representation of the parse trees.
- They do not provide every characteristic information from the real syntax.
- For example- no rule nodes, no parenthesis etc.
PRACTICE PROBLEMS BASED ON SYNTAX TREES-
Problem-01:
Considering the following grammar-
E → E + T | T
T → T x F | F
F → ( E ) | id
Generate the following for the string id + id x id
- Parse tree
- Syntax tree
- Directed Acyclic Graph (DAG)
Solution-
Parse Tree-
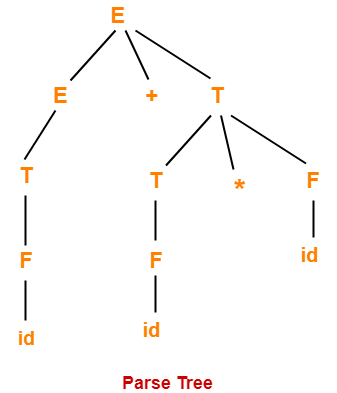
Syntax Tree-
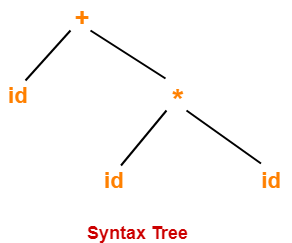
Directed Acyclic Graph-

Also Read- Directed Acyclic Graphs
Problem-02:
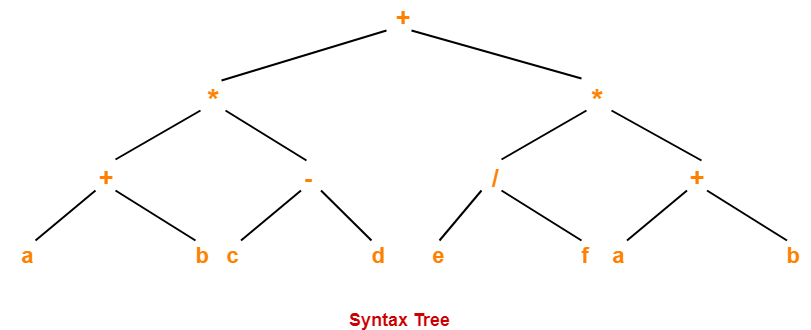
Construct a syntax tree for the following arithmetic expression-
( a + b ) * ( c – d ) + ( ( e / f ) * ( a + b ))
Solution-
Step-01:
We convert the given arithmetic expression into a postfix expression as-
( a + b ) * ( c – d ) + ( ( e / f ) * ( a + b ) )
ab+ * ( c – d ) + ( ( e / f ) * ( a + b ) )
ab+ * cd- + ( ( e / f ) * ( a + b ) )
ab+ * cd- + ( ef/ * ( a + b ) )
ab+ * cd- + ( ef/ * ab+ )
ab+ * cd- + ef/ab+*
ab+cd-* + ef/ab+*
ab+cd-*ef/ab+*+
Step-02:
We draw a syntax tree for the above postfix expression.
Steps Involved
Start pushing the symbols of the postfix expression into the stack one by one. When an operand is encountered,
When an operator is encountered
Continue in the similar manner and draw the syntax tree simultaneously. |
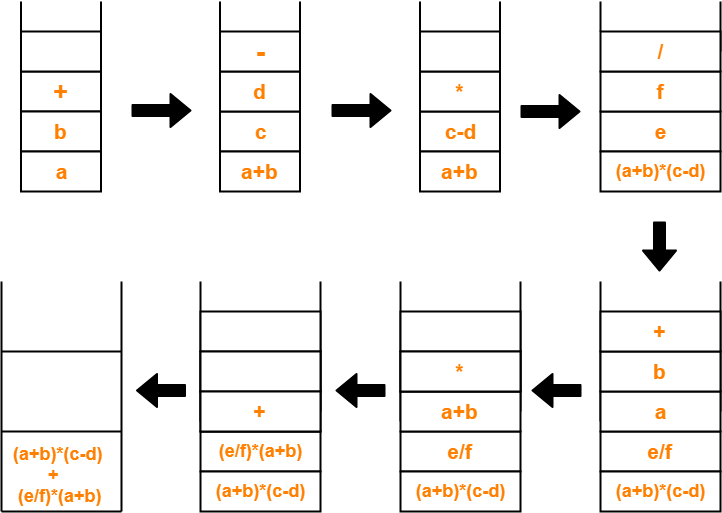
The required syntax tree is-
To gain better understanding about Syntax Trees,
Download Handwritten Notes Here-
Next Article- Shift Reduce Parsing
Get more notes and other study material of Compiler Design.
Watch video lectures by visiting our YouTube channel LearnVidFun.
