Directed Acyclic Graphs | DAGs | Examples

Directed Acyclic Graph-

 

Directed Acyclic Graph (DAG) is a special kind of Abstract Syntax Tree.

 

• Each node of it contains a unique value.
• It does not contain any cycles in it, hence called Acyclic.

 

Optimization Of Basic Blocks-

 

DAG is a very useful data structure for implementing transformations on Basic Blocks.

 

• A DAG is constructed for optimizing the basic block.
• A DAG is usually constructed using Three Address Code.
• Transformations such as dead code elimination and common sub expression elimination are then applied.

 

Properties-

 

• Reachability relation forms a partial order in DAGs.
• Both transitive closure & transitive reduction are uniquely defined for DAGs.
• Topological Orderings are defined for DAGs.

 

Applications-

 

DAGs are used for the following purposes-

• To determine the expressions which have been computed more than once (called common sub-expressions).
• To determine the names whose computation has been done outside the block but used inside the block.
• To determine the statements of the block whose computed value can be made available outside the block.
• To simplify the list of Quadruples by not executing the assignment instructions x:=y unless they are necessary and eliminating the common sub-expressions.

 

Construction of DAGs-

 

Following rules are used for the construction of DAGs-

 

Rule-01:

 

In a DAG,

• Interior nodes always represent the operators.
• Exterior nodes (leaf nodes) always represent the names, identifiers or constants.

 

Rule-02:

 

While constructing a DAG,

• A check is made to find if there exists any node with the same value.
• A new node is created only when there does not exist any node with the same value.
• This action helps in detecting the common sub-expressions and avoiding the re-computation of the same.

 

Rule-03:

 

The assignment instructions of the form x:=y are not performed unless they are necessary.

 

Also Read- Code Optimization

 

PRACTICE PROBLEMS BASED ON DIRECTED ACYCLIC GRAPHS-

 

Problem-01:

 

Consider the following expression and construct a DAG for it-

         ( a + b ) x ( a + b + c )

 

Solution-

 

Three Address Code for the given expression is-

 

T1 = a + b

T2 = T1 + c

T3 = T1 x T2

 

Now, Directed Acyclic Graph is-

 

 

NOTE   From the constructed DAG, we observe- The common sub-expression (a+b) has been expressed into a single node in the DAG. The computation is carried out only once and stored in the identifier T1 and reused later.   This illustrates how the construction scheme of a DAG identifies the common sub-expression and helps in eliminating its re-computation later.

 

Problem-02:

 

Consider the following expression and construct a DAG for it-

( ( ( a + a ) + ( a + a ) ) + ( ( a + a ) + ( a + a ) ) )

 

Solution-

 

Directed Acyclic Graph for the given expression is-

 

 

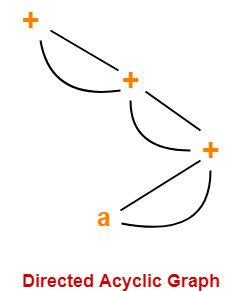
Problem-03:

 

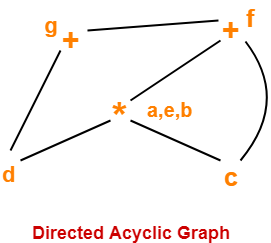
Consider the following block and construct a DAG for it-

 

(1) a = b x c

(2) d = b

(3) e = d x c

(4) b = e

(5) f = b + c

(6) g = f + d

 

Solution-

 

Directed Acyclic Graph for the given block is-

 

 

Problem-04:

 

Optimize the block in the Problem-03.

 

Solution-

 

Step-01:

 

Firstly, construct a DAG for the given block (already done above).

 

Step-02:

 

Now, the optimized block can be generated by traversing the DAG.

• The common sub-expression e = d x c which is actually b x c (since d = b) is eliminated.
• The dead code b = e is eliminated.

 

The optimized block is-

 

(1) a = b x c

(2) d = b

(3) f = a + c

(4) g = f + d

 

Problem-05:

 

Consider the following basic block-

 

B10:

S1 = 4 x I

S2 = addr(A) – 4

S3 = S2[S1]

S4 = 4 x I

S5 = addr(B) – 4

S6 = S5[S4]

S7 = S3 x S6

S8 = PROD + S7

PROD = S8

S9 = I + 1

I = S9

If I <= 20 goto L10

 

1. Draw a directed acyclic graph and identify local common sub-expressions.
2. After eliminating the common sub-expressions, re-write the basic block.

 

Solution-

 

Directed Acyclic Graph for the given basic block is-

 

 

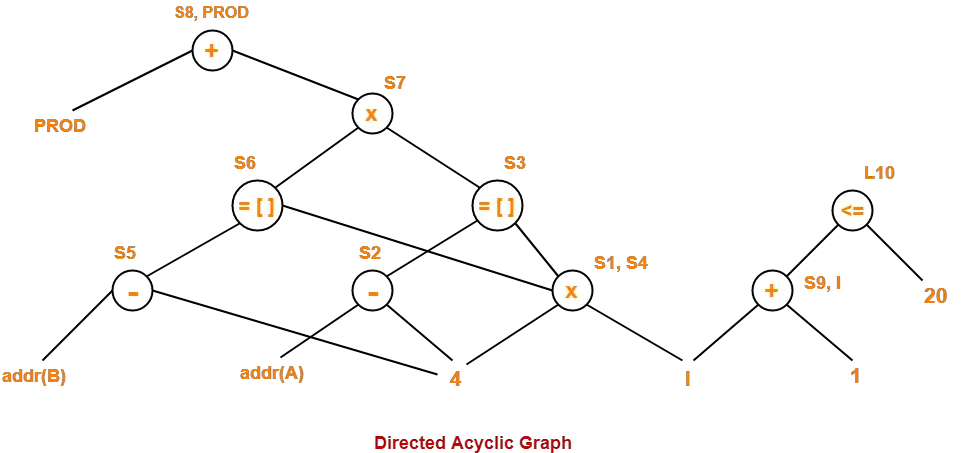
In this code fragment,

• 4 x I is a common sub-expression. Hence, we can eliminate because S1 = S4.
• We can optimize S8 = PROD + S7 and PROD = S8 as PROD = PROD + S7.
• We can optimize S9 = I + 1 and I = S9 as I = I + 1.

 

After eliminating S4, S8 and S9, we get the following basic block-

 

B10:

S1 = 4 x I

S2 = addr(A) – 4

S3 = S2[S1]

S5 = addr(B) – 4

S6 = S5[S1]

S7 = S3 x S6

PROD = PROD + S7

I = I + 1

If I <= 20 goto L10

 

To gain  better understanding about Directed Acyclic Graphs,

Watch this Video Lecture

 

Download Handwritten Notes Here-

 

 

Next Article- Misc Problems On Directed Acyclic Graphs

 

Get more notes and other study material of Compiler Design.

Watch video lectures by visiting our YouTube channel LearnVidFun.