Paging in OS-
Before you go through this article, make sure that you have gone through the previous articles on Paging in OS.
We have discussed-
- Paging is a non-contiguous memory allocation technique.
- Page Table is a table that maps a page number to the frame number containing that page.
- Multilevel Paging is a paging scheme where there exists a hierarchy of page tables.
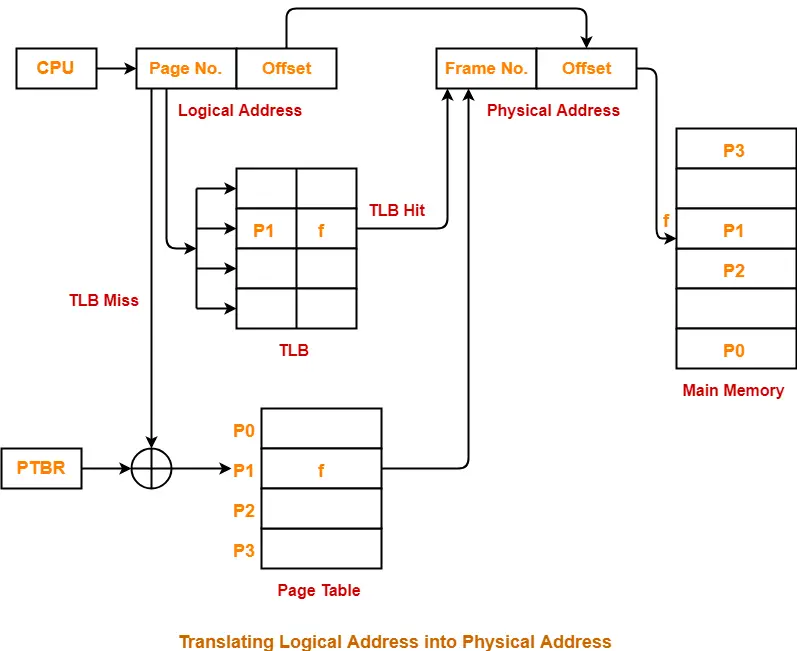
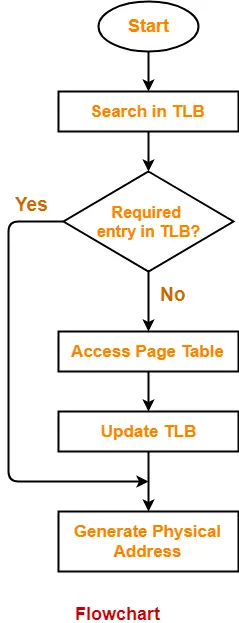
- Translation Lookaside Buffer tries to reduce the effective access time.
Also Read- Important Formulas of Paging
In this article, we will discuss practice problems based on multilevel paging using TLB.
Effective Access Time-
In a multilevel paging scheme using TLB, the effective access time is given by-

This formula is valid only when there are no Page Faults.
PRACTICE PROBLEMS BASED ON MULTILEVEL PAGING AND TLB-
Problem-01:
Consider a single level paging scheme with a TLB. Assume no page fault occurs. It takes 20 ns to search the TLB and 100 ns to access the physical memory. If TLB hit ratio is 80%, the effective memory access time is _______ msec.
Solution-
Given-
- Number of levels of page table = 1
- TLB access time = 20 ns
- Main memory access time = 100 ns
- TLB Hit ratio = 80% = 0.8
Calculating TLB Miss Ratio-
TLB Miss ratio
= 1 – TLB Hit ratio
= 1 – 0.8
= 0.2
Calculating Effective Access Time-
Substituting values in the above formula, we get-
Effective Access Time
= 0.8 x { 20 ns + 100 ns } + 0.2 x { 20 ns + (1+1) x 100 ns }
= 0.8 x 120 ns + 0.2 + 220 ns
= 96 ns + 44 ns
= 140 ns
Thus, effective memory access time = 140 ns.
Problem-02:
Consider a two level paging scheme with a TLB. Assume no page fault occurs. It takes 20 ns to search the TLB and 100 ns to access the physical memory. If TLB hit ratio is 80%, the effective memory access time is _______ msec.
Solution-
Given-
- Number of levels of page table = 2
- TLB access time = 20 ns
- Main memory access time = 100 ns
- TLB Hit ratio = 80% = 0.8
Calculating TLB Miss Ratio-
TLB Miss ratio
= 1 – TLB Hit ratio
= 1 – 0.8
= 0.2
Calculating Effective Access Time-
Substituting values in the above formula, we get-
Effective Access Time
= 0.8 x { 20 ns + 100 ns } + 0.2 x { 20 ns + (2+1) x 100 ns }
= 0.8 x 120 ns + 0.2 + 320 ns
= 96 ns + 64 ns
= 160 ns
Thus, effective memory access time = 160 ns.
Problem-03:
Consider a three level paging scheme with a TLB. Assume no page fault occurs. It takes 20 ns to search the TLB and 100 ns to access the physical memory. If TLB hit ratio is 80%, the effective memory access time is _______ msec.
Solution-
Given-
- Number of levels of page table = 3
- TLB access time = 20 ns
- Main memory access time = 100 ns
- TLB Hit ratio = 80% = 0.8
Calculating TLB Miss Ratio-
TLB Miss ratio
= 1 – TLB Hit ratio
= 1 – 0.8
= 0.2
Calculating Effective Access Time-
Substituting values in the above formula, we get-
Effective Access Time
= 0.8 x { 20 ns + 100 ns } + 0.2 x { 20 ns + (3+1) x 100 ns }
= 0.8 x 120 ns + 0.2 + 420 ns
= 96 ns + 84 ns
= 180 ns
Thus, effective memory access time = 180 ns.
Problem-04:
Consider a single level paging scheme with a TLB. Assume no page fault occurs. It takes 20 ns to search the TLB and 100 ns to access the physical memory. If effective memory access time is 130 ns, TLB hit ratio is ______.
Solution-
Given-
- Number of levels of page table = 1
- TLB access time = 20 ns
- Main memory access time = 100 ns
- Effective memory access time = 130 ns
Let TLB Hit ratio = H
Calculating TLB Miss Ratio-
TLB Miss ratio
= 1 – TLB Hit ratio
= 1 – H
Calculating TLB Hit Ratio-
Substituting values in the above formula, we get-
130 ns = H x { 20 ns + 100 ns } + (1-H) x { 20 ns + (1+1) x 100 ns }
130 ns = H x { 120 ns } + (1-H) x { 220 ns }
130 ns = 120H ns + 220 ns – 220H ns
220H ns – 120H ns = 220 ns – 130 ns
100H ns = 90 ns
H = 90 / 100
∴ H = 0.9
Thus, TLB hit ratio = 0.9 or 90%.
Problem-05:
Consider a single level paging scheme with a TLB. Assume no page fault occurs. It takes 100 ns to access the physical memory. If TLB hit ratio is 60% and effective memory access time is 160 ns, TLB access time is ______.
Solution-
Given-
- Number of levels of page table = 1
- Main memory access time = 100 ns
- TLB Hit ratio = 60% = 0.6
- Effective memory access time = 160 ns
Let TLB access time = T ns
Calculating TLB Miss Ratio-
TLB Miss ratio
= 1 – TLB Hit ratio
= 1 – 0.6
= 0.4
Calculating TLB Access Time-
Substituting values in the above formula, we get-
160 ns = 0.6 x { T ns + 100 ns } + 0.4 x { T ns + (1+1) x 100 ns }
160 ns = 0.6 x { T ns + 100 ns } + 0.4 x { T ns + 200 ns }
160 ns = 0.6T ns + 60 ns + 0.4T ns + 80 ns
0.6T ns + 0.4T ns = 160 ns – 60 ns – 80 ns
T ns = 20 ns
∴ T = 20
Thus, TLB access time = 20 ns.
Problem-06:
Consider a single level paging scheme with a TLB. Assume no page fault occurs. It takes 20 ns to search the TLB. If TLB hit ratio is 50% and effective memory access time is 170 ns, main memory access time is ______.
Solution-
Given-
- Number of levels of page table = 1
- TLB access time = 20 ns
- TLB Hit ratio = 50% = 0.5
- Effective memory access time = 170 ns
Let main memory access time = T ns
Calculating TLB Miss Ratio-
TLB Miss ratio
= 1 – TLB Hit ratio
= 1 – 0.5
= 0.5
Calculating Main Memory Access Time-
Substituting values in the above formula, we get-
170 ns = 0.5 x { 20 ns + T ns } + 0.5 x { 20 ns + (1+1) x T ns }
170 ns = 0.5 x { 20 ns + T ns } + 0.5 x { 20 ns + 2T ns }
170 ns = 10 ns + 0.5T ns + 10 ns + T ns
0.5T ns + T ns = 170 ns – 10 ns – 10 ns
1.5T ns = 150 ns
T = 150 / 1.5
∴ T = 100
Thus, Main Memory access time = 100 ns.
Next Article- Page Faults in OS
Get more notes and other study material of Operating System.
Watch video lectures by visiting our YouTube channel LearnVidFun.