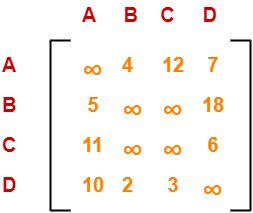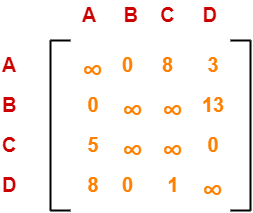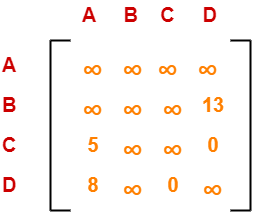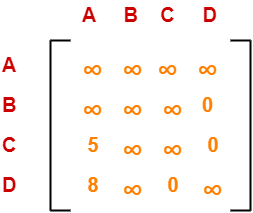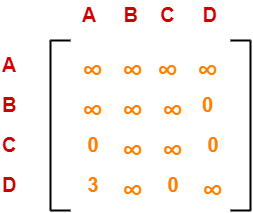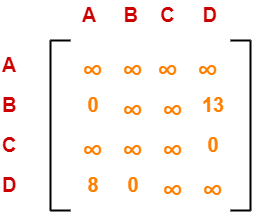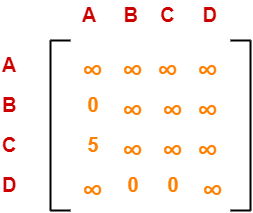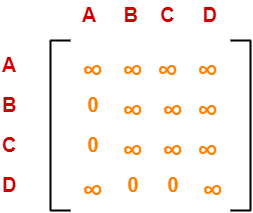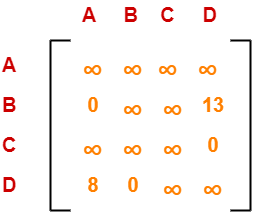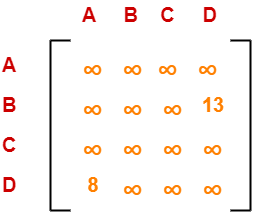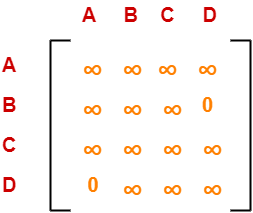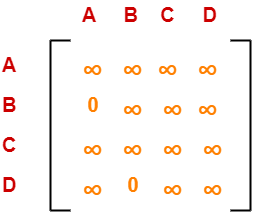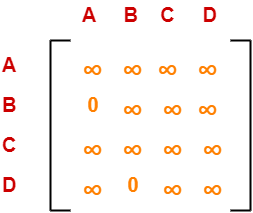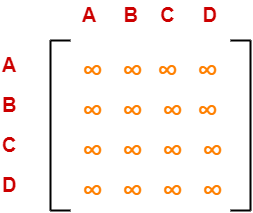April, 2018 | Gate Vidyalay

Month: April 2018

Decomposition in DBMS | Lossless | Lossy

Decomposition of a Relation-

The process of breaking up or dividing a single relation into two or more sub relations is called as decomposition of a relation.

Properties of Decomposition-

The following two properties must be followed when decomposing a given relation-

1. Lossless decomposition-

Lossless decomposition ensures-

No information is lost from the original relation during decomposition.
When the sub relations are joined back, the same relation is obtained that was decomposed.

Every decomposition must always be lossless.

2. Dependency Preservation-

Dependency preservation ensures-

None of the functional dependencies that holds on the original relation are lost.
The sub relations still hold or satisfy the functional dependencies of the original relation.

Types of Decomposition-

Decomposition of a relation can be completed in the following two ways-

1. Lossless Join Decomposition-

Consider there is a relation R which is decomposed into sub relations R₁ , R₂ , …. , R_n.
This decomposition is called lossless join decomposition when the join of the sub relations results in the same relation R that was decomposed.
For lossless join decomposition, we always have-

R₁ ⋈ R₂ ⋈ R₃ ……. ⋈ R_n = R

where ⋈ is a natural join operator

Example-

Consider the following relation R( A , B , C )-

A	B	C
1	2	1
2	5	3
3	3	3

R( A , B , C )

Consider this relation is decomposed into two sub relations R₁( A , B ) and R₂( B , C )-

The two sub relations are-

A	B
1	2
2	5
3	3

R₁( A , B )

B	C
2	1
5	3
3	3

R₂( B , C )

Now, let us check whether this decomposition is lossless or not.

For lossless decomposition, we must have-

R₁ ⋈ R₂ = R

Now, if we perform the natural join ( ⋈ ) of the sub relations R₁ and R₂ ,we get-

A	B	C
1	2	1
2	5	3
3	3	3

This relation is same as the original relation R.

Thus, we conclude that the above decomposition is lossless join decomposition.

NOTE-

Lossless join decomposition is also known as non-additive join decomposition.
This is because the resultant relation after joining the sub relations is same as the decomposed relation.
No extraneous tuples appear after joining of the sub-relations.

2. Lossy Join Decomposition-

Consider there is a relation R which is decomposed into sub relations R₁ , R₂ , …. , R_n.
This decomposition is called lossy join decomposition when the join of the sub relations does not result in the same relation R that was decomposed.
The natural join of the sub relations is always found to have some extraneous tuples.
For lossy join decomposition, we always have-

R₁ ⋈ R₂ ⋈ R₃ ……. ⋈ R_n ⊃ R

where ⋈ is a natural join operator

Example-

Consider the following relation R( A , B , C )-

A	B	C
1	2	1
2	5	3
3	3	3

R( A , B , C )

Consider this relation is decomposed into two sub relations as R₁( A , C ) and R₂( B , C )-

The two sub relations are-

A	C
1	1
2	3
3	3

R₁( A , B )

B	C
2	1
5	3
3	3

R₂( B , C )

Now, let us check whether this decomposition is lossy or not.

For lossy decomposition, we must have-

R₁ ⋈ R₂ ⊃ R

Now, if we perform the natural join ( ⋈ ) of the sub relations R₁ and R₂we get-

A	B	C
1	2	1
2	5	3
2	3	3
3	5	3
3	3	3

This relation is not same as the original relation R and contains some extraneous tuples.

Clearly, R₁ ⋈ R₂ ⊃ R.

Thus, we conclude that the above decomposition is lossy join decomposition.

NOTE-

Lossy join decomposition is also known as careless decomposition.
This is because extraneous tuples get introduced in the natural join of the sub-relations.
Extraneous tuples make the identification of the original tuples difficult.

Next Article- Rules to Determine Lossless and Lossy Decomposition

Get more notes and other study material of Database Management System (DBMS).

Watch video lectures by visiting our YouTube channel LearnVidFun.

Equivalence of Two Sets of Functional Dependencies

Database Management System

Equivalence of Two Sets of Functional Dependencies-

Before you go through this article, make sure that you have gone through the previous article on Functional Dependency.

In DBMS,

Two different sets of functional dependencies for a given relation may or may not be equivalent.
If F and G are the two sets of functional dependencies, then following 3 cases are possible-

Case-01: F covers G (F ⊇ G)

Case-02: G covers F (G ⊇ F)

Case-03: Both F and G cover each other (F = G)

Case-01: Determining Whether F Covers G-

Following steps are followed to determine whether F covers G or not-

Step-01:

Take the functional dependencies of set G into consideration.
For each functional dependency X → Y, find the closure of X using the functional dependencies of set G.

Step-02:

Take the functional dependencies of set G into consideration.
For each functional dependency X → Y, find the closure of X using the functional dependencies of set F.

Step-03:

Compare the results of Step-01 and Step-02.
If the functional dependencies of set F has determined all those attributes that were determined by the functional dependencies of set G, then it means F covers G.
Thus, we conclude F covers G (F ⊇ G) otherwise not.

Case-02: Determining Whether G Covers F-

Following steps are followed to determine whether G covers F or not-

Step-01:

Take the functional dependencies of set F into consideration.
For each functional dependency X → Y, find the closure of X using the functional dependencies of set F.

Step-02:

Take the functional dependencies of set F into consideration.
For each functional dependency X → Y, find the closure of X using the functional dependencies of set G.

Step-03:

Compare the results of Step-01 and Step-02.
If the functional dependencies of set G has determined all those attributes that were determined by the functional dependencies of set F, then it means G covers F.
Thus, we conclude G covers F (G ⊇ F) otherwise not.

Case-03: Determining Whether Both F and G Cover Each Other-

If F covers G and G covers F, then both F and G cover each other.
Thus, if both the above cases hold true, we conclude both F and G cover each other (F = G).

PRACTICE PROBLEM BASED ON EQUIVALENCE OF FUNCTIONAL DEPENDENCIES-

Problem-

A relation R (A , C , D , E , H) is having two functional dependencies sets F and G as shown-

Set F-

A → C

AC → D

E → AD

E → H

Set G-

A → CD

E → AH

Which of the following holds true?

(A) G ⊇ F

(B) F ⊇ G

(D) All of the above

Solution-

Determining whether F covers G-

Step-01:

(A)⁺ = { A , C , D } // closure of left side of A → CD using set G
(E)⁺ = { A , C , D , E , H } // closure of left side of E → AH using set G

Step-02:

(A)⁺ = { A , C , D } // closure of left side of A → CD using set F
(E)⁺ = { A , C , D , E , H } // closure of left side of E → AH using set F

Step-03:

Comparing the results of Step-01 and Step-02, we find-

Functional dependencies of set F can determine all the attributes which have been determined by the functional dependencies of set G.
Thus, we conclude F covers G i.e. F ⊇ G.

Determining whether G covers F-

Step-01:

(A)⁺ = { A , C , D } // closure of left side of A → C using set F
(AC)⁺ = { A , C , D } // closure of left side of AC → D using set F
(E)⁺ = { A , C , D , E , H } // closure of left side of E → AD and E → H using set F

Step-02:

(A)⁺ = { A , C , D } // closure of left side of A → C using set G
(AC)⁺ = { A , C , D } // closure of left side of AC → D using set G
(E)⁺ = { A , C , D , E , H } // closure of left side of E → AD and E → H using set G

Step-03:

Comparing the results of Step-01 and Step-02, we find-

Functional dependencies of set G can determine all the attributes which have been determined by the functional dependencies of set F.
Thus, we conclude G covers F i.e. G ⊇ F.

Determining whether both F and G cover each other-

From Step-01, we conclude F covers G.
From Step-02, we conclude G covers F.
Thus, we conclude both F and G cover each other i.e. F = G.

Thus, Option (D) is correct.

Next Article- Canonical Cover in DBMS

Get more notes and other study material of Database Management System (DBMS).

Watch video lectures by visiting our YouTube channel LearnVidFun.

Normalization in DBMS | Normal Forms

Database Management System

Normalization in DBMS-

In DBMS, database normalization is a process of making the database consistent by-

Reducing the redundancies
Ensuring the integrity of data through lossless decomposition

Normalization is done through normal forms.

Normal Forms-

The standard normal forms used are-

First Normal Form (1NF)
Second Normal Form (2NF)
Third Normal Form (3NF)
Boyce-Codd Normal Form (BCNF)

There exists several other normal forms even after BCNF but generally we normalize till BCNF only.

First Normal Form-

A given relation is called in First Normal Form (1NF) if each cell of the table contains only an atomic value.

A given relation is called in First Normal Form (1NF) if the attribute of every tuple is either single valued or a null value.

Example-

The following relation is not in 1NF-

Student_id	Name	Subjects
100	Akshay	Computer Networks, Designing
101	Aman	Database Management System
102	Anjali	Automata, Compiler Design

Relation is not in 1NF

However,

This relation can be brought into 1NF.
This can be done by rewriting the relation such that each cell of the table contains only one value.

Student_id	Name	Subjects
100	Akshay	Computer Networks
100	Akshay	Designing
101	Aman	Database Management System
102	Anjali	Automata
102	Anjali	Compiler Design

Relation is in 1NF

This relation is in First Normal Form (1NF).

NOTE-

By default, every relation is in 1NF.
This is because formal definition of a relation states that value of all the attributes must be atomic.

Second Normal Form-

A given relation is called in Second Normal Form (2NF) if and only if-

Relation already exists in 1NF.
No partial dependency exists in the relation.

Also Read- Functional Dependency in DBMS

Partial Dependency

A partial dependency is a dependency where few attributes of the candidate key determines non-prime attribute(s).

A partial dependency is a dependency where a portion of the candidate key or incomplete candidate key determines non-prime attribute(s).

In other words,

A → B is called a partial dependency if and only if-

A is a subset of some candidate key
B is a non-prime attribute.

If any one condition fails, then it will not be a partial dependency.

NOTE-

To avoid partial dependency, incomplete candidate key must not determine any non-prime attribute.
However, incomplete candidate key can determine prime attributes.

Also Read- How To Find Candidate Keys?

Example-

Consider a relation- R ( V , W , X , Y , Z ) with functional dependencies-

VW → XY

Y → V

WX → YZ

The possible candidate keys for this relation are-

VW , WX , WY

From here,

Prime attributes = { V , W , X , Y }
Non-prime attributes = { Z }

Now, if we observe the given dependencies-

There is no partial dependency.
This is because there exists no dependency where incomplete candidate key determines any non-prime attribute.

Thus, we conclude that the given relation is in 2NF.

Third Normal Form-

A given relation is called in Third Normal Form (3NF) if and only if-

Relation already exists in 2NF.
No transitive dependency exists for non-prime attributes.

Transitive Dependency

A → B is called a transitive dependency if and only if-

A is not a super key.
B is a non-prime attribute.

If any one condition fails, then it is not a transitive dependency.

NOTE-

Transitive dependency must not exist for non-prime attributes.
However, transitive dependency can exist for prime attributes.

A relation is called in Third Normal Form (3NF) if and only if-

Any one condition holds for each non-trivial functional dependency A → B

A is a super key
B is a prime attribute

Example-

Consider a relation- R ( A , B , C , D , E ) with functional dependencies-

A → BC

CD → E

B → D

E → A

The possible candidate keys for this relation are-

A , E , CD , BC

From here,

Prime attributes = { A , B , C , D , E }
There are no non-prime attributes

Now,

It is clear that there are no non-prime attributes in the relation.
In other words, all the attributes of relation are prime attributes.
Thus, all the attributes on RHS of each functional dependency are prime attributes.

Thus, we conclude that the given relation is in 3NF.

Boyce-Codd Normal Form-

A given relation is called in BCNF if and only if-

Relation already exists in 3NF.
For each non-trivial functional dependency A → B, A is a super key of the relation.

Example-

Consider a relation- R ( A , B , C ) with the functional dependencies-

A → B

B → C

C → A

The possible candidate keys for this relation are-

A , B , C

Now, we can observe that RHS of each given functional dependency is a candidate key.

Thus, we conclude that the given relation is in BCNF.

Next Article- Important Points About Normal Forms

Get more notes and other study material of Database Management System (DBMS).

Watch video lectures by visiting our YouTube channel LearnVidFun.

Travelling Salesman Problem | Branch & Bound

Design & Analysis of Algorithms

Travelling Salesman Problem-

You are given-

A set of some cities
Distance between every pair of cities

Travelling Salesman Problem states-

A salesman has to visit every city exactly once.
He has to come back to the city from where he starts his journey.
What is the shortest possible route that the salesman must follow to complete his tour?

Example-

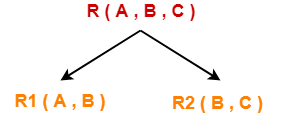
The following graph shows a set of cities and distance between every pair of cities-

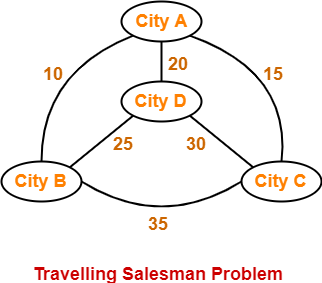
If salesman starting city is A, then a TSP tour in the graph is-

A → B → D → C → A

Cost of the tour

= 10 + 25 + 30 + 15

= 80 units

In this article, we will discuss how to solve travelling salesman problem using branch and bound approach with example.

PRACTICE PROBLEM BASED ON TRAVELLING SALESMAN PROBLEM USING BRANCH AND BOUND APPROACH-

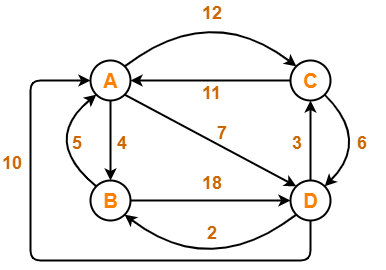
Problem-

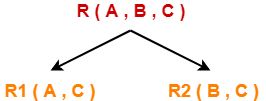
Solve Travelling Salesman Problem using Branch and Bound Algorithm in the following graph-

Solution-

Step-01:

Write the initial cost matrix and reduce it-

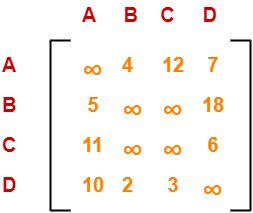
Rules

To reduce a matrix, perform the row reduction and column reduction of the matrix separately.
A row or a column is said to be reduced if it contains at least one entry ‘0’ in it.

Row Reduction-

Consider the rows of above matrix one by one.

If the row already contains an entry ‘0’, then-

There is no need to reduce that row.

If the row does not contains an entry ‘0’, then-

Reduce that particular row.
Select the least value element from that row.
Subtract that element from each element of that row.
This will create an entry ‘0’ in that row, thus reducing that row.

Following this, we have-

Reduce the elements of row-1 by 4.
Reduce the elements of row-2 by 5.
Reduce the elements of row-3 by 6.
Reduce the elements of row-4 by 2.

Performing this, we obtain the following row-reduced matrix-

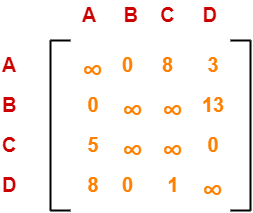
Column Reduction-

Consider the columns of above row-reduced matrix one by one.

If the column already contains an entry ‘0’, then-

There is no need to reduce that column.

If the column does not contains an entry ‘0’, then-

Reduce that particular column.
Select the least value element from that column.
Subtract that element from each element of that column.
This will create an entry ‘0’ in that column, thus reducing that column.

Following this, we have-

There is no need to reduce column-1.
There is no need to reduce column-2.
Reduce the elements of column-3 by 1.
There is no need to reduce column-4.

Performing this, we obtain the following column-reduced matrix-

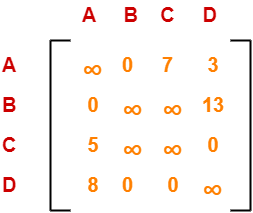
Finally, the initial distance matrix is completely reduced.

Now, we calculate the cost of node-1 by adding all the reduction elements.

Cost(1)

= Sum of all reduction elements

= 4 + 5 + 6 + 2 + 1

= 18

Step-02:

We consider all other vertices one by one.
We select the best vertex where we can land upon to minimize the tour cost.

Choosing To Go To Vertex-B: Node-2 (Path A → B)

From the reduced matrix of step-01, M[A,B] = 0
Set row-A and column-B to ∞
Set M[B,A] = ∞

Now, resulting cost matrix is-

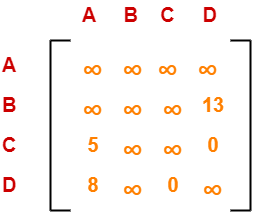
Now,

We reduce this matrix.
Then, we find out the cost of node-02.

Row Reduction-

We can not reduce row-1 as all its elements are ∞.
Reduce all the elements of row-2 by 13.
There is no need to reduce row-3.
There is no need to reduce row-4.

Performing this, we obtain the following row-reduced matrix-

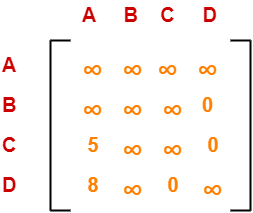
Column Reduction-

Reduce the elements of column-1 by 5.
We can not reduce column-2 as all its elements are ∞.
There is no need to reduce column-3.
There is no need to reduce column-4.

Performing this, we obtain the following column-reduced matrix-

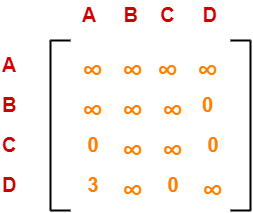
Finally, the matrix is completely reduced.

Now, we calculate the cost of node-2.

Cost(2)

= Cost(1) + Sum of reduction elements + M[A,B]

= 18 + (13 + 5) + 0

= 36

Choosing To Go To Vertex-C: Node-3 (Path A → C)

From the reduced matrix of step-01, M[A,C] = 7
Set row-A and column-C to ∞
Set M[C,A] = ∞

Now, resulting cost matrix is-

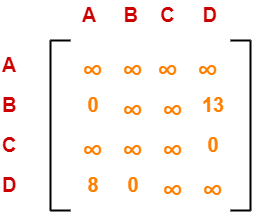
Now,

We reduce this matrix.
Then, we find out the cost of node-03.

Row Reduction-

We can not reduce row-1 as all its elements are ∞.
There is no need to reduce row-2.
There is no need to reduce row-3.
There is no need to reduce row-4.

Thus, the matrix is already row-reduced.

Column Reduction-

There is no need to reduce column-1.
There is no need to reduce column-2.
We can not reduce column-3 as all its elements are ∞.
There is no need to reduce column-4.

Thus, the matrix is already column reduced.

Finally, the matrix is completely reduced.

Now, we calculate the cost of node-3.

Cost(3)

= Cost(1) + Sum of reduction elements + M[A,C]

= 18 + 0 + 7

= 25

Choosing To Go To Vertex-D: Node-4 (Path A → D)

From the reduced matrix of step-01, M[A,D] = 3
Set row-A and column-D to ∞
Set M[D,A] = ∞

Now, resulting cost matrix is-

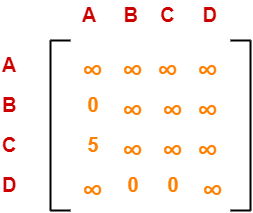
Now,

We reduce this matrix.
Then, we find out the cost of node-04.

Row Reduction-

We can not reduce row-1 as all its elements are ∞.
There is no need to reduce row-2.
Reduce all the elements of row-3 by 5.
There is no need to reduce row-4.

Performing this, we obtain the following row-reduced matrix-

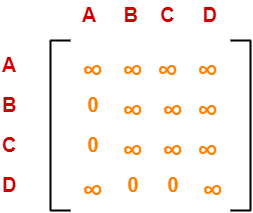
Column Reduction-

There is no need to reduce column-1.
There is no need to reduce column-2.
There is no need to reduce column-3.
We can not reduce column-4 as all its elements are ∞.

Thus, the matrix is already column-reduced.

Finally, the matrix is completely reduced.

Now, we calculate the cost of node-4.

Cost(4)

= Cost(1) + Sum of reduction elements + M[A,D]

= 18 + 5 + 3

= 26

Thus, we have-

Cost(2) = 36 (for Path A → B)
Cost(3) = 25 (for Path A → C)
Cost(4) = 26 (for Path A → D)

We choose the node with the lowest cost.

Since cost for node-3 is lowest, so we prefer to visit node-3.

Thus, we choose node-3 i.e. path A → C.

Step-03:

We explore the vertices B and D from node-3.

We now start from the cost matrix at node-3 which is-

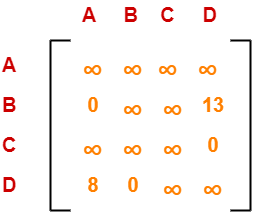
Cost(3) = 25

Choosing To Go To Vertex-B: Node-5 (Path A → C → B)

From the reduced matrix of step-02, M[C,B] = ∞
Set row-C and column-B to ∞
Set M[B,A] = ∞

Now, resulting cost matrix is-

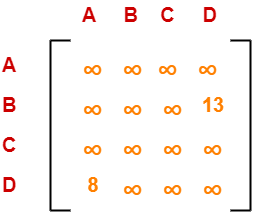
Now,

We reduce this matrix.
Then, we find out the cost of node-5.

Row Reduction-

We can not reduce row-1 as all its elements are ∞.
Reduce all the elements of row-2 by 13.
We can not reduce row-3 as all its elements are ∞.
Reduce all the elements of row-4 by 8.

Performing this, we obtain the following row-reduced matrix-

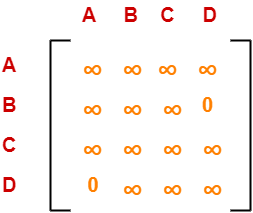
Column Reduction-

There is no need to reduce column-1.
We can not reduce column-2 as all its elements are ∞.
We can not reduce column-3 as all its elements are ∞.
There is no need to reduce column-4.

Thus, the matrix is already column reduced.

Finally, the matrix is completely reduced.

Now, we calculate the cost of node-5.

Cost(5)

= cost(3) + Sum of reduction elements + M[C,B]

= 25 + (13 + 8) + ∞

= ∞

Choosing To Go To Vertex-D: Node-6 (Path A → C → D)

From the reduced matrix of step-02, M[C,D] = ∞
Set row-C and column-D to ∞
Set M[D,A] = ∞

Now, resulting cost matrix is-

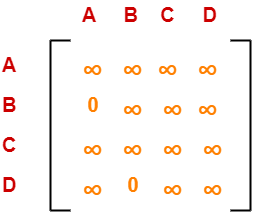
Now,

We reduce this matrix.
Then, we find out the cost of node-6.

Row Reduction-

We can not reduce row-1 as all its elements are ∞.
There is no need to reduce row-2.
We can not reduce row-3 as all its elements are ∞.
We can not reduce row-4 as all its elements are ∞.

Thus, the matrix is already row reduced.

Column Reduction-

There is no need to reduce column-1.
We can not reduce column-2 as all its elements are ∞.
We can not reduce column-3 as all its elements are ∞.
We can not reduce column-4 as all its elements are ∞.

Thus, the matrix is already column reduced.

Finally, the matrix is completely reduced.

Now, we calculate the cost of node-6.

Cost(6)

= cost(3) + Sum of reduction elements + M[C,D]

= 25 + 0 + 0

= 25

Thus, we have-

Cost(5) = ∞ (for Path A → C → B)
Cost(6) = 25 (for Path A → C → D)

We choose the node with the lowest cost.

Since cost for node-6 is lowest, so we prefer to visit node-6.

Thus, we choose node-6 i.e. path C → D.

Step-04:

We explore vertex B from node-6.

We start with the cost matrix at node-6 which is-

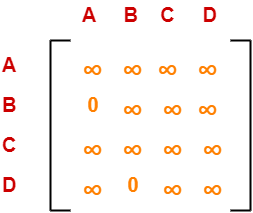
Cost(6) = 25

Choosing To Go To Vertex-B: Node-7 (Path A → C → D → B)

From the reduced matrix of step-03, M[D,B] = 0
Set row-D and column-B to ∞
Set M[B,A] = ∞

Now, resulting cost matrix is-

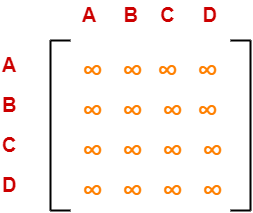
Now,

We reduce this matrix.
Then, we find out the cost of node-7.

Row Reduction-

We can not reduce row-1 as all its elements are ∞.
We can not reduce row-2 as all its elements are ∞.
We can not reduce row-3 as all its elements are ∞.
We can not reduce row-4 as all its elements are ∞.

Column Reduction-

We can not reduce column-1 as all its elements are ∞.
We can not reduce column-2 as all its elements are ∞.
We can not reduce column-3 as all its elements are ∞.
We can not reduce column-4 as all its elements are ∞.

Thus, the matrix is already column reduced.

Finally, the matrix is completely reduced.

All the entries have become ∞.

Now, we calculate the cost of node-7.

Cost(7)

= cost(6) + Sum of reduction elements + M[D,B]

= 25 + 0 + 0

= 25

Thus,

Optimal path is: A → C → D → B → A
Cost of Optimal path = 25 units

To gain better understanding about Travelling Salesman Problem,

Watch this Video Lecture

Get more notes and other study material of Design and Analysis of Algorithms.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Data Structures Test on Binary Search Trees

Data Structures Tests

[mtouchquiz 2]

← Older Posts

Newer Posts →