Breadth First Search-
- Breadth First Search or BFS is a graph traversal algorithm.
- It is used for traversing or searching a graph in a systematic fashion.
- BFS uses a strategy that searches in the graph in breadth first manner whenever possible.
- Queue data structure is used in the implementation of breadth first search.
BFS Example-
Consider the following graph-
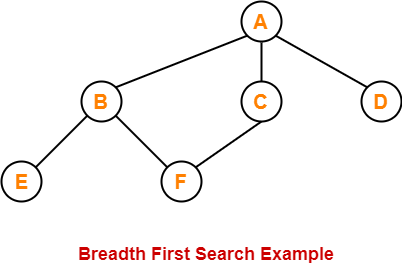
The breadth first search traversal order of the above graph is-
A, B, C, D, E, F
Breadth First Search Algorithm-
BFS (V,E,s)
for each vertex v in V – {s}
do
color[v] ← WHITE
d[v] ← ∞
π[v] ← NIL
color[s] = GREY
d[s] ← 0
π[s] ← NIL
Q ← { }
ENQUEUE (Q,s)
While Q is non-empty
do v ← DEQUEUE (Q)
for each u adjacent to v
do if color[u] ← WHITE
then color[u] ← GREY
d[u] ← d[v] + 1
π[u] ← v
ENQUEUE (Q,u)
color[v] ← BLACK
Explanation-
The above breadth first search algorithm is explained in the following steps-
Step-01
Create and maintain 3 variables for each vertex of the graph. For any vertex ‘v’ of the graph, these 3 variables are-
1. color[v]-
2. Π[v]-
This variable represents the predecessor of vertex ‘v’.
3. d[v]-
This variable represents the distance of vertex v from the source vertex.
Step-02
For each vertex v of the graph except source vertex, initialize the variables as-
For source vertex S, initialize the variables as-
Step-03
Now, enqueue source vertex S in queue Q and repeat the following procedure until the queue Q becomes empty- 1. Dequeue vertex v from queue Q. 2. For all the adjacent white vertices u of vertex v, do- color[u] = GREY d[u] = d[v] + 1 π[u] = v Enqueue (Q,u) 3. Color vertex v to black. |
BFS Time Complexity-
The total running time for Breadth First Search is O (V+E).
Also Read- Depth First Search
PRACTICE PROBLEM BASED ON BREADTH FIRST SEARCH-
Problem-
Traverse the following graph using Breadth First Search Technique-
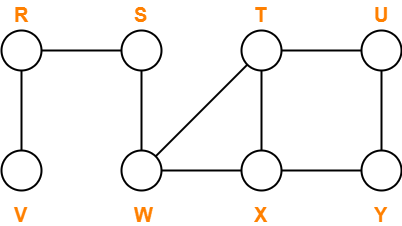
Consider vertex S as the starting vertex.
Solution-
Step-01:
For all the vertices v except source vertex S of the graph, we initialize the variables as-
- color[v] = WHITE
- π[v] = NIL
- d[v] = ∞
For source vertex S, we initialize the variables as-
- color[S] = GREY
- π[S] = NIL
- d[S] = 0
We enqueue the source vertex S in the queue Q.
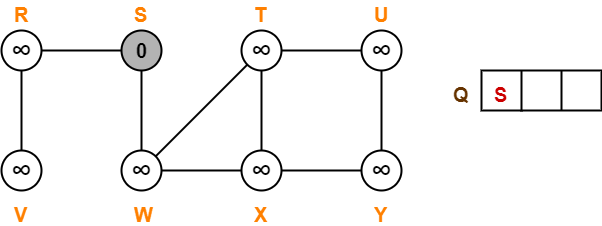
Step-02:
- Dequeue vertex S from the queue Q
- For all adjacent white vertices ‘v’ (vertices R and W) of vertex S, we do-
- color[v] = GREY
- d[v] = d[S] + 1 = 0 + 1 = 1
- π[v] = S
- Enqueue all adjacent white vertices of S in queue Q
- color[S] = BLACK
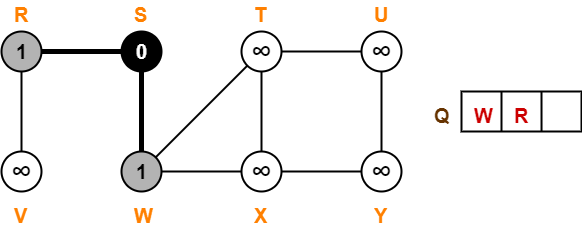
Step-03:
- Dequeue vertex W from the queue Q
- For all adjacent white vertices ‘v’ (vertices T and X) of vertex W, we do-
- color[v] = GREY
- d[v] = d[W] + 1 = 1 + 1 = 2
- π[v] = W
- Enqueue all adjacent white vertices of W in queue Q
- color[W] = BLACK
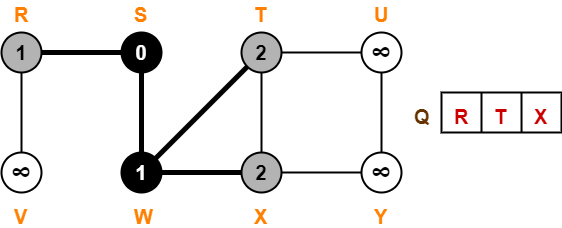
Step-04:
- Dequeue vertex R from the queue Q
- For all adjacent white vertices ‘v’ (vertex V) of vertex R, we do-
- color[v] = GREY
- d[v] = d[R] + 1 = 1 + 1 = 2
- π[v] = R
- Enqueue all adjacent white vertices of R in queue Q
- color[R] = BLACK
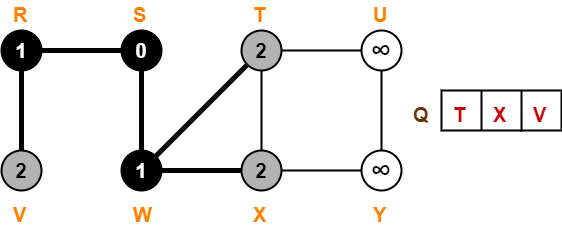
Step-05:
- Dequeue vertex T from the queue Q
- For all adjacent white vertices ‘v’ (vertex U) of vertex T, we do-
- color[v] = GREY
- d[v] = d[T] + 1 = 2 + 1 = 3
- π[v] = T
- Enqueue all adjacent white vertices of T in queue Q
- color[T] = BLACK
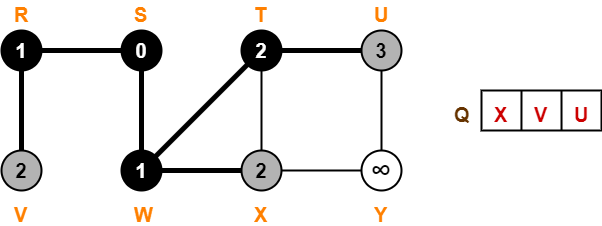
Step-06:
- Dequeue vertex X from the queue Q
- For all adjacent white vertices ‘v’ (vertex Y) of vertex X, we do-
- color[v] = GREY
- d[v] = d[X] + 1 = 2 + 1 = 3
- π[v] = X
- Enqueue all adjacent white vertices of X in queue Q
- color[X] = BLACK
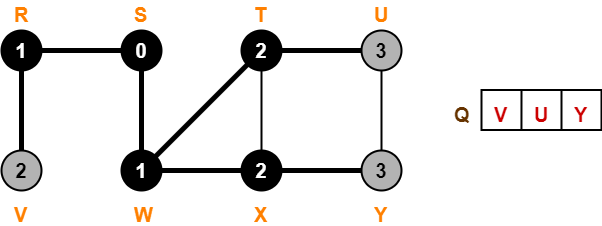
Step-07:
- Dequeue vertex V from the queue Q
- There are no adjacent white vertices to vertex V.
- color[V] = BLACK
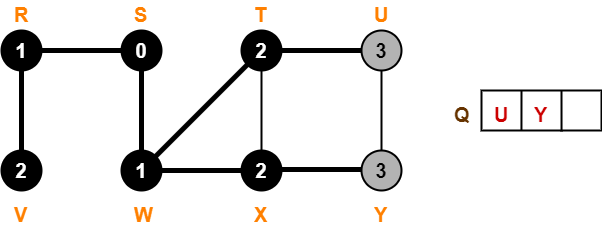
Step-08:
- Dequeue vertex U from the queue Q
- There are no adjacent white vertices to vertex U.
- color[U] = BLACK
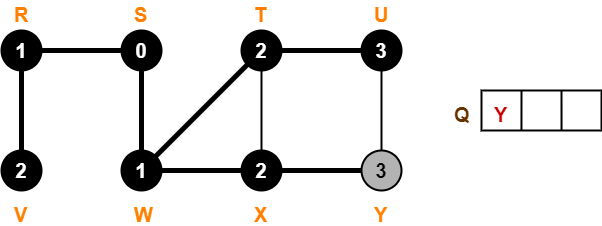
Step-09:
- Dequeue vertex Y from the queue Q
- There are no adjacent white vertices to vertex Y.
- color[Y] = BLACK
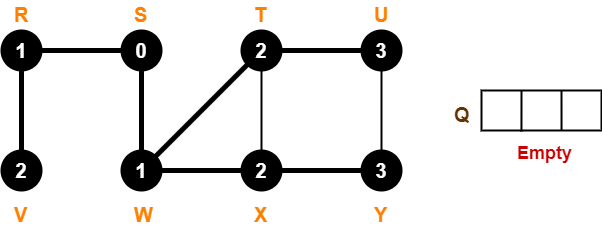
Since, all the vertices have turned black and the queue has got empty, so we stop.
This is how any given graph is traversed using Breadth First Search (BFS) technique.
To gain better understanding about Breadth First Search Algorithm,
Next Article- Prim’s Algorithm
Get more notes and other study material of Design and Analysis of Algorithms.
Watch video lectures by visiting our YouTube channel LearnVidFun.