Construction Of DFA-
Before you go through this article, make sure that you have gone through the previous article on Type-01 Problems.
Type-02 Problems-
In Type-02 problems, we will discuss the construction of DFA for languages consisting of strings starting with a particular substring.
Steps To Construct DFA-
Following steps are followed to construct a DFA for Type-02 problems-
Step-01:
- Determine the minimum number of states required in the DFA.
- Draw those states.
Use the following rule to determine the minimum number of states-
RULECalculate the length of substring. All strings starting with ‘n’ length substring will always require minimum (n+2) states in the DFA. |
Step-02:
- Decide the strings for which DFA will be constructed.
- The method for deciding the strings has been discussed in this Video.
Step-03:
- Construct a DFA for the strings decided in Step-02.
Remember the following rule while constructing the DFA-
RULEWhile constructing a DFA,
|
Step-04:
- Send all the left possible combinations to the dead state.
- Do not send the left possible combinations over the starting state.
PRACTICE PROBLEMS BASED ON CONSTRUCTION OF DFA-
Problem-01:
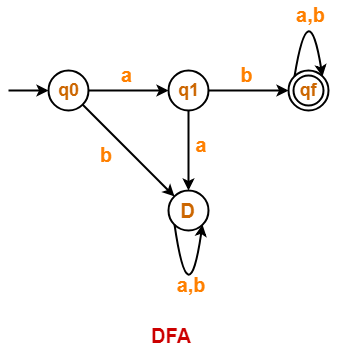
Draw a DFA for the language accepting strings starting with ‘ab’ over input alphabets ∑ = {a, b}
Solution-
Regular expression for the given language = ab(a + b)*
Step-01:
- All strings of the language starts with substring “ab”.
- So, length of substring = 2.
Thus, Minimum number of states required in the DFA = 2 + 2 = 4.
It suggests that minimized DFA will have 4 states.
Step-02:
We will construct DFA for the following strings-
- ab
- aba
- abab
Step-03:
The required DFA is-
Problem-02:
Draw a DFA for the language accepting strings starting with ‘a’ over input alphabets ∑ = {a, b}
Solution-
Regular expression for the given language = a(a + b)*
Step-01:
- All strings of the language starts with substring “a”.
- So, length of substring = 1.
Thus, Minimum number of states required in the DFA = 1 + 2 = 3.
It suggests that minimized DFA will have 3 states.
Step-02:
We will construct DFA for the following strings-
- a
- aa
Step-03:
The required DFA is-
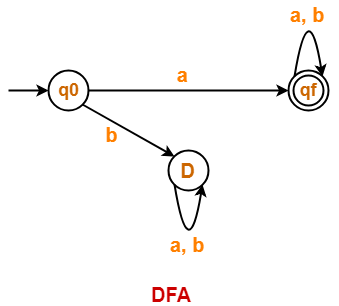
Problem-03:
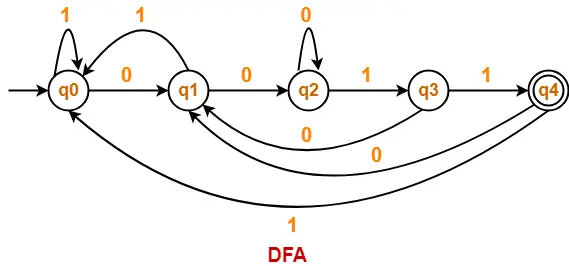
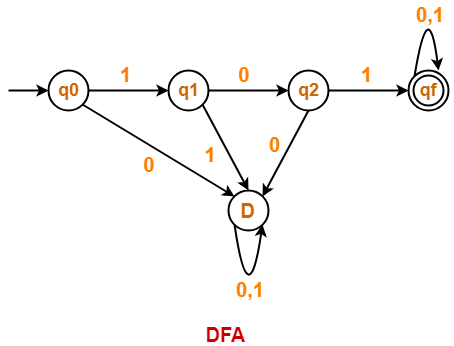
Draw a DFA for the language accepting strings starting with ‘101’ over input alphabets ∑ = {0, 1}
Solution-
Regular expression for the given language = 101(0 + 1)*
Step-01:
- All strings of the language starts with substring “101”.
- So, length of substring = 3.
Thus, Minimum number of states required in the DFA = 3 + 2 = 5.
It suggests that minimized DFA will have 5 states.
Step-02:
We will construct DFA for the following strings-
- 101
- 1011
- 10110
- 101101
Step-03:
The required DFA is-
Problem-04:
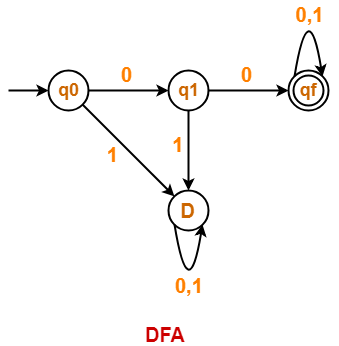
Draw a DFA that accepts a language L over input alphabets ∑ = {0, 1} such that L is the set of all strings starting with ’00’.
Solution-
Regular expression for the given language = 00(0 + 1)*
Step-01:
- All strings of the language starts with substring “00”.
- So, length of substring = 2.
Thus, Minimum number of states required in the DFA = 2 + 2 = 4.
It suggests that minimized DFA will have 4 states.
Step-02:
We will construct DFA for the following strings-
- 00
- 000
- 00000
Step-03:
The required DFA is-
Problem-05:
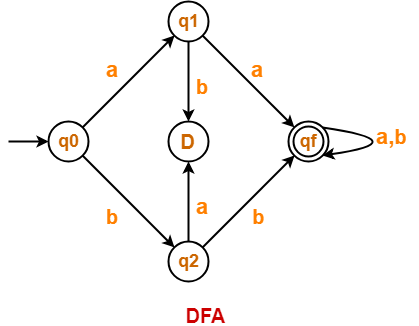
Construct a DFA that accepts a language L over input alphabets ∑ = {a, b} such that L is the set of all strings starting with ‘aa’ or ‘bb’.
Solution-
Regular expression for the given language = (aa + bb)(a + b)*
Step-01:
Minimum number of states required in the DFA = 5.
It suggests that minimized DFA will have 5 states.
Step-02:
We will construct DFA for the following strings-
- aa
- aaa
- aaaa
- bb
- bbb
- bbbb
Step-03:
The required DFA is-
Problem-06:
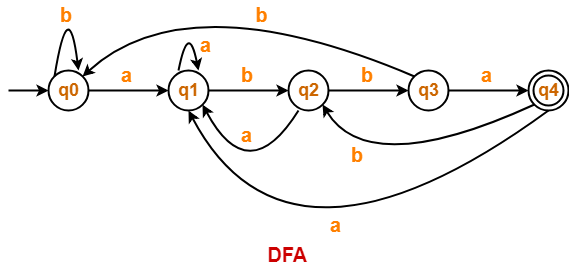
Construct a DFA that accepts a language L over input alphabets ∑ = {a, b} such that L is the set of all strings starting with ‘aba’.
Solution-
Regular expression for the given language = aba(a + b)*
Step-01:
- All strings of the language starts with substring “aba”.
- So, length of substring = 3.
Thus, Minimum number of states required in the DFA = 3 + 2 = 5.
It suggests that minimized DFA will have 5 states.
Step-02:
We will construct DFA for the following strings-
- aba
- abaa
- abaab
- abaaba
Step-03:
The required DFA is-

Also Read- Converting DFA to Regular Expression
To gain better understanding about Construction of DFA,
Download Handwritten Notes Here-
Next Article- Minimization of DFA
Get more notes and other study material of Theory of Automata and Computation.
Watch video lectures by visiting our YouTube channel LearnVidFun.