AVL Tree-
Before you go through this article, make sure that you have gone through the previous article on AVL Trees.
We have discussed-
- AVL trees are self-balancing binary search trees.
- In AVL trees, balancing factor of each node is either 0 or 1 or -1.
In this article, we will discuss insertion in AVL tree.
Insertion in AVL Tree-
| Insertion Operation is performed to insert an element in the AVL Tree. |
To insert an element in the AVL tree, follow the following steps-
- Insert the element in the AVL tree in the same way the insertion is performed in BST.
- After insertion, check the balance factor of each node of the resulting tree.
Read More- Insertion in Binary Search Tree
Now, following two cases are possible-
Case-01:
- After the insertion, the balance factor of each node is either 0 or 1 or -1.
- In this case, the tree is considered to be balanced.
- Conclude the operation.
- Insert the next element if any.
Case-02:
- After the insertion, the balance factor of at least one node is not 0 or 1 or -1.
- In this case, the tree is considered to be imbalanced.
- Perform the suitable rotation to balance the tree.
- After the tree is balanced, insert the next element if any.
Also Read- AVL Tree Properties
Rules To Remember-
Rule-01:
After inserting an element in the existing AVL tree,
- Balance factor of only those nodes will be affected that lies on the path from the newly inserted node to the root node.
Rule-02:
To check whether the AVL tree is still balanced or not after the insertion,
- There is no need to check the balance factor of every node.
- Check the balance factor of only those nodes that lies on the path from the newly inserted node to the root node.
Rule-03:
After inserting an element in the AVL tree,
- If tree becomes imbalanced, then there exists one particular node in the tree by balancing which the entire tree becomes balanced automatically.
- To re balance the tree, balance that particular node.
To find that particular node,
- Traverse the path from the newly inserted node to the root node.
- Check the balance factor of each node that is encountered while traversing the path.
- The first encountered imbalanced node will be the node that needs to be balanced.
To balance that node,
- Count three nodes in the direction of leaf node.
- Then, use the concept of AVL tree rotations to re balance the tree.
PRACTICE PROBLEM BASED ON AVL TREE INSERTION-
Problem-
Construct AVL Tree for the following sequence of numbers-
50 , 20 , 60 , 10 , 8 , 15 , 32 , 46 , 11 , 48
Solution-
Step-01: Insert 50

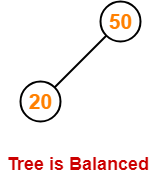
Step-02: Insert 20
- As 20 < 50, so insert 20 in 50’s left sub tree.
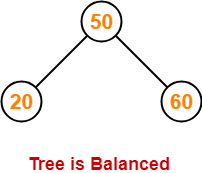
Step-03: Insert 60
- As 60 > 50, so insert 60 in 50’s right sub tree.
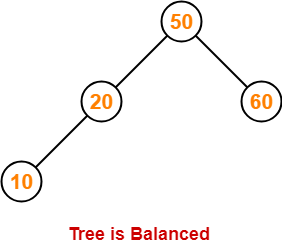
Step-04: Insert 10
- As 10 < 50, so insert 10 in 50’s left sub tree.
- As 10 < 20, so insert 10 in 20’s left sub tree.
Step-05: Insert 8
- As 8 < 50, so insert 8 in 50’s left sub tree.
- As 8 < 20, so insert 8 in 20’s left sub tree.
- As 8 < 10, so insert 8 in 10’s left sub tree.
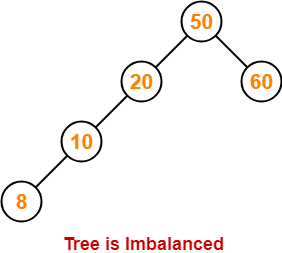
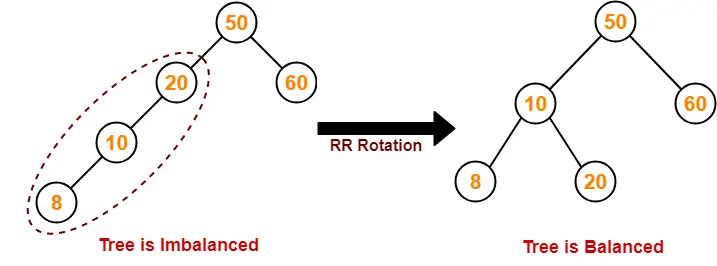
To balance the tree,
- Find the first imbalanced node on the path from the newly inserted node (node 8) to the root node.
- The first imbalanced node is node 20.
- Now, count three nodes from node 20 in the direction of leaf node.
- Then, use AVL tree rotation to balance the tree.
Following this, we have-
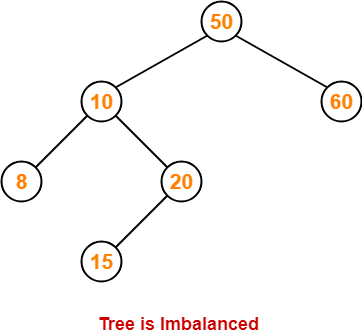
Step-06: Insert 15
- As 15 < 50, so insert 15 in 50’s left sub tree.
- As 15 > 10, so insert 15 in 10’s right sub tree.
- As 15 < 20, so insert 15 in 20’s left sub tree.
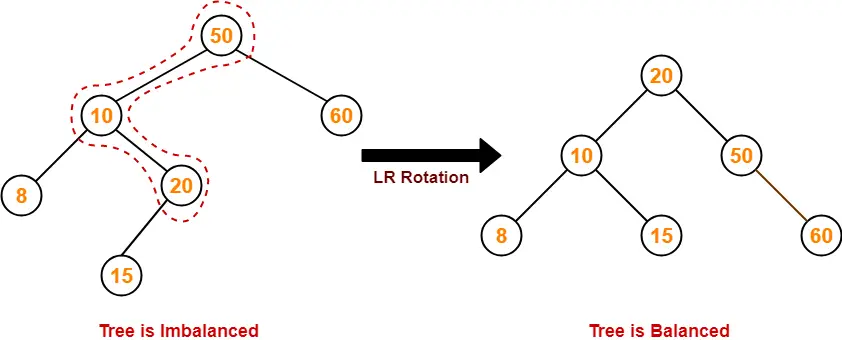
To balance the tree,
- Find the first imbalanced node on the path from the newly inserted node (node 15) to the root node.
- The first imbalanced node is node 50.
- Now, count three nodes from node 50 in the direction of leaf node.
- Then, use AVL tree rotation to balance the tree.
Following this, we have-
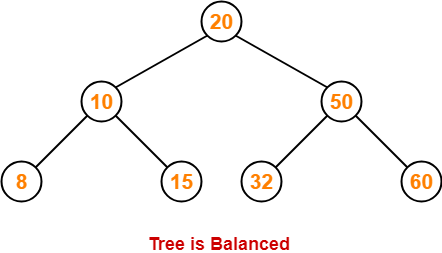
Step-07: Insert 32
- As 32 > 20, so insert 32 in 20’s right sub tree.
- As 32 < 50, so insert 32 in 50’s left sub tree.
Step-08: Insert 46
- As 46 > 20, so insert 46 in 20’s right sub tree.
- As 46 < 50, so insert 46 in 50’s left sub tree.
- As 46 > 32, so insert 46 in 32’s right sub tree.
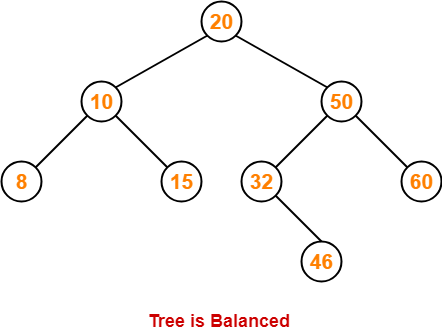
Step-09: Insert 11
- As 11 < 20, so insert 11 in 20’s left sub tree.
- As 11 > 10, so insert 11 in 10’s right sub tree.
- As 11 < 15, so insert 11 in 15’s left sub tree.
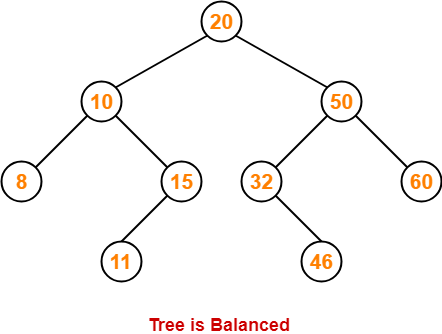
Step-10: Insert 48
- As 48 > 20, so insert 48 in 20’s right sub tree.
- As 48 < 50, so insert 48 in 50’s left sub tree.
- As 48 > 32, so insert 48 in 32’s right sub tree.
- As 48 > 46, so insert 48 in 46’s right sub tree.
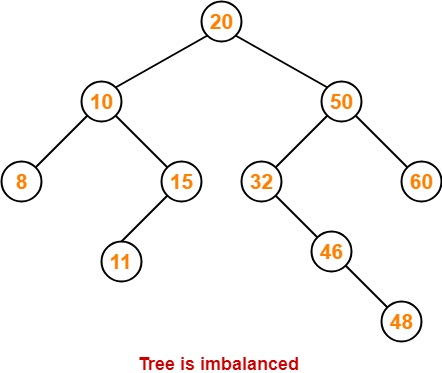
To balance the tree,
- Find the first imbalanced node on the path from the newly inserted node (node 48) to the root node.
- The first imbalanced node is node 32.
- Now, count three nodes from node 32 in the direction of leaf node.
- Then, use AVL tree rotation to balance the tree.
Following this, we have-

This is the final balanced AVL tree after inserting all the given elements.
To gain better understanding of AVL Tree Insertion,
Next Article- Heap Data Structure
Get more notes and other study material of Data Structures.
Watch video lectures by visiting our YouTube channel LearnVidFun.