AVL Tree Insertion | Insertion in AVL Tree

AVL Tree-

 

Before you go through this article, make sure that you have gone through the previous article on AVL Trees.

 

We have discussed-

• AVL trees are self-balancing binary search trees.
• In AVL trees, balancing factor of each node is either 0 or 1 or -1.

 

In this article, we will discuss insertion in AVL tree.

 

Insertion in AVL Tree-

 

Insertion Operation is performed to insert an element in the AVL Tree.

 

To insert an element in the AVL tree, follow the following steps-

• Insert the element in the AVL tree in the same way the insertion is performed in BST.
• After insertion, check the balance factor of each node of the resulting tree.

 

Read More- Insertion in Binary Search Tree

 

Now, following two cases are possible-

 

Case-01:

 

• After the insertion, the balance factor of each node is either 0 or 1 or -1.
• In this case, the tree is considered to be balanced.
• Conclude the operation.
• Insert the next element if any.

 

Case-02:

 

• After the insertion, the balance factor of at least one node is not 0 or 1 or -1.
• In this case, the tree is considered to be imbalanced.
• Perform the suitable rotation to balance the tree.
• After the tree is balanced, insert the next element if any.

 

Also Read- AVL Tree Properties

 

Rules To Remember-

 

Rule-01:

 

After inserting an element in the existing AVL tree,

• Balance factor of only those nodes will be affected that lies on the path from the newly inserted node to the root node.

 

Rule-02:

 

To check whether the AVL tree is still balanced or not after the insertion,

• There is no need to check the balance factor of every node.
• Check the balance factor of only those nodes that lies on the path from the newly inserted node to the root node.

 

Rule-03:

 

After inserting an element in the AVL tree,

• If tree becomes imbalanced, then there exists one particular node in the tree by balancing which the entire tree becomes balanced automatically.
• To re balance the tree, balance that particular node.

 

To find that particular node,

• Traverse the path from the newly inserted node to the root node.
• Check the balance factor of each node that is encountered while traversing the path.
• The first encountered imbalanced node will be the node that needs to be balanced.

 

To balance that node,

• Count three nodes in the direction of leaf node.
• Then, use the concept of AVL tree rotations to re balance the tree.

 

PRACTICE PROBLEM BASED ON AVL TREE INSERTION-

 

Problem-

 

Construct AVL Tree for the following sequence of numbers-

50 , 20 , 60 , 10 , 8 , 15 , 32 , 46 , 11 , 48

 

Solution-

 

Step-01: Insert 50

 

 

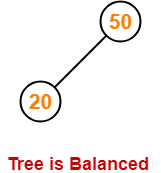
Step-02: Insert 20

 

• As 20 < 50, so insert 20 in 50’s left sub tree.

 

 

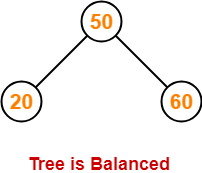
Step-03: Insert 60

 

• As 60 > 50, so insert 60 in 50’s right sub tree.

 

 

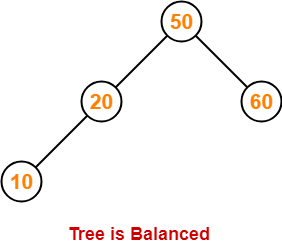
Step-04: Insert 10

 

• As 10 < 50, so insert 10 in 50’s left sub tree.
• As 10 < 20, so insert 10 in 20’s left sub tree.

 

 

Step-05: Insert 8

 

• As 8 < 50, so insert 8 in 50’s left sub tree.
• As 8 < 20, so insert 8 in 20’s left sub tree.
• As 8 < 10, so insert 8 in 10’s left sub tree.

 

 

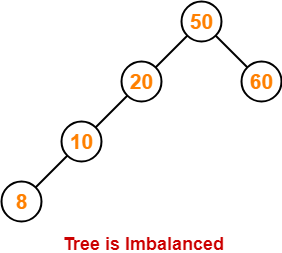
To balance the tree,

• Find the first imbalanced node on the path from the newly inserted node (node 8) to the root node.
• The first imbalanced node is node 20.
• Now, count three nodes from node 20 in the direction of leaf node.
• Then, use AVL tree rotation to balance the tree.

 

Following this, we have-

 

 

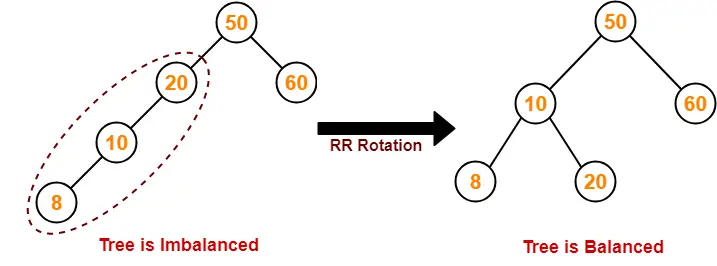
Step-06: Insert 15

 

• As 15 < 50, so insert 15 in 50’s left sub tree.
• As 15 > 10, so insert 15 in 10’s right sub tree.
• As 15 < 20, so insert 15 in 20’s left sub tree.

 

 

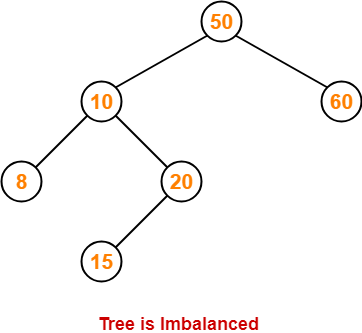
To balance the tree,

• Find the first imbalanced node on the path from the newly inserted node (node 15) to the root node.
• The first imbalanced node is node 50.
• Now, count three nodes from node 50 in the direction of leaf node.
• Then, use AVL tree rotation to balance the tree.

 

Following this, we have-

 

 

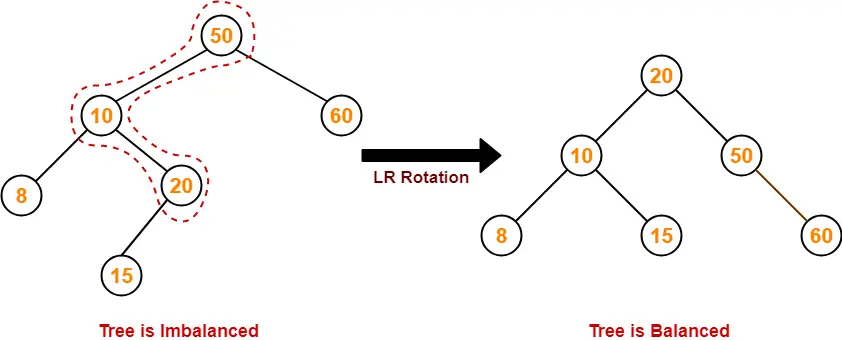
Step-07: Insert 32

 

• As 32 > 20, so insert 32 in 20’s right sub tree.
• As 32 < 50, so insert 32 in 50’s left sub tree.

 

 

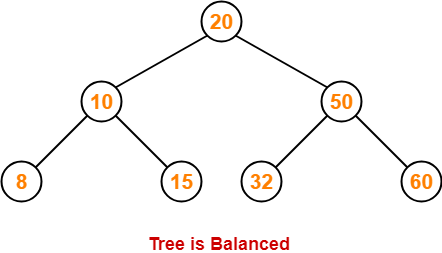
Step-08: Insert 46

 

• As 46 > 20, so insert 46 in 20’s right sub tree.
• As 46 < 50, so insert 46 in 50’s left sub tree.
• As 46 > 32, so insert 46 in 32’s right sub tree.

 

 

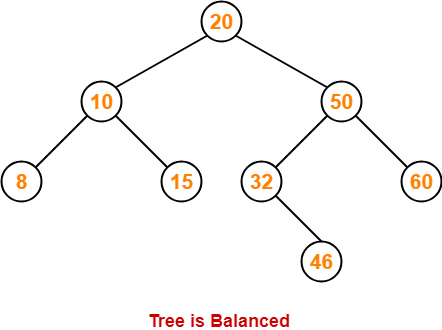
Step-09: Insert 11

 

• As 11 < 20, so insert 11 in 20’s left sub tree.
• As 11 > 10, so insert 11 in 10’s right sub tree.
• As 11 < 15, so insert 11 in 15’s left sub tree.

 

 

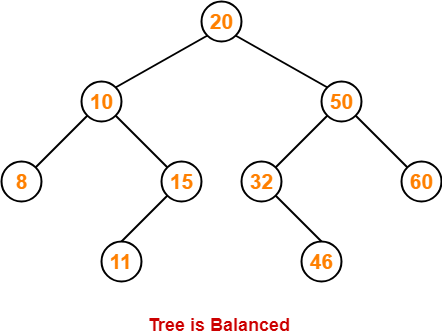
Step-10: Insert 48

 

• As 48 > 20, so insert 48 in 20’s right sub tree.
• As 48 < 50, so insert 48 in 50’s left sub tree.
• As 48 > 32, so insert 48 in 32’s right sub tree.
• As 48 > 46, so insert 48 in 46’s right sub tree.

 

 

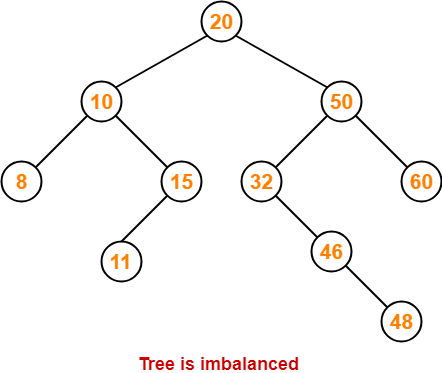
To balance the tree,

• Find the first imbalanced node on the path from the newly inserted node (node 48) to the root node.
• The first imbalanced node is node 32.
• Now, count three nodes from node 32 in the direction of leaf node.
• Then, use AVL tree rotation to balance the tree.

 

Following this, we have-

 

 

This is the final balanced AVL tree after inserting all the given elements.

 

To gain better understanding of AVL Tree Insertion,

Watch this Video Lecture

 

Next Article- Heap Data Structure

 

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.