Heap Data Structure | Binary Heap | Examples

Heap Data Structure-

 

In data structures,

• Heap is a specialized data structure.
• It has special characteristics.
• A heap may be implemented using a n-ary tree.

 

In this article, we will discuss implementation of heap using a binary tree.

 

Binary Heap-

 

A binary heap is a Binary Tree with the following two properties-

 

 

• Ordering Property
• Structural Property

 

1. Ordering Property-

 

By this property,

• Elements in the heap tree are arranged in specific order.
• This gives rise to two types of heaps- min heap and max heap.

 

2. Structural Property-

 

By this property,

• Binary heap is an almost complete binary tree.
• It has all its levels completely filled except possibly the last level.
• The last level is strictly filled from left to right.

 

Types of Binary Heap-

 

Depending on the arrangement of elements, a binary heap may be of following two types-

 

 

1. Max Heap
2. Min Heap

 

1. Max Heap-

 

• Max Heap conforms to the above properties of heap.
• In max heap, every node contains greater or equal value element than its child nodes.
• Thus, root node contains the largest value element.

 

Example-

 

Consider the following example of max heap-

 

 

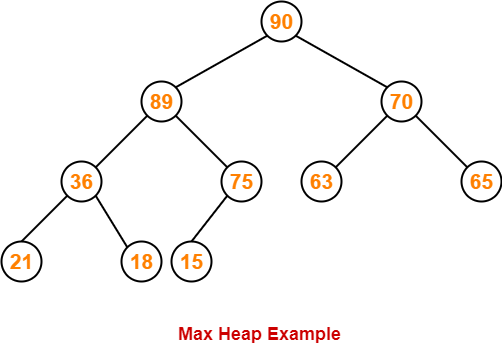
This is max heap because-

• Every node contains greater or equal value element than its child nodes.
• It is an almost complete binary tree with its last level strictly filled from left to right.

 

2. Min Heap-

 

• Min Heap conforms to the above properties of heap.
• In min heap, every node contains lesser value element than its child nodes.
• Thus, root node contains the smallest value element.

 

Example-

 

Consider the following example of min heap-

 

 

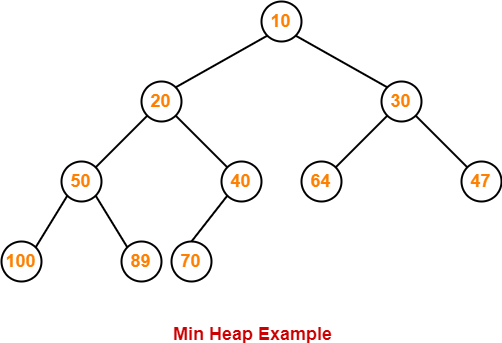
This is min heap because-

• Every node contains lesser value element than its child nodes.
• It is an almost complete binary tree with its last level strictly filled from left to right.

 

Array Representation of Binary Heap-

 

A binary heap is typically represented as an array.

 

 

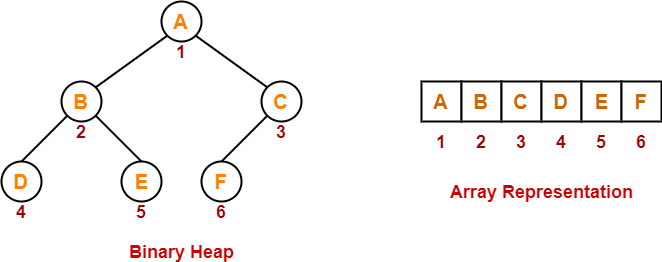
For a node present at index ‘i’ of the array Arr-

 

If indexing starts with 0,

• Its parent node will be present at array location = Arr [ i/2 ]
• Its left child node will be present at array location = Arr [ 2i+1 ]
• Its right child node will be present at array location = Arr [ 2i+2 ]

 

If indexing starts with 1,

• Its parent node will be present at array location = Arr [ ⌊i/2⌋ ]
• Its left child node will be present at array location = Arr [ 2i ]
• Its right child node will be present at array location = Arr [ 2i+1 ]

 

Important Notes-

 

Note-01:

 

• Level order traversal technique may be used to achieve the array representation of a heap tree.
• Array representation of a heap never contains any empty indices in between.
• However, array representation of a binary tree may contain some empty indices in between.

 

Note-02:

 

Given an array representation of a binary heap,

• If all the elements are in descending order, then heap is definitely a max heap.
• If all the elements are not in descending order, then it may or may not be a max heap.
• If all the elements are in ascending order, then heap is definitely a min heap.
• If all the elements are not in ascending order, then it may or may not be a min heap.

 

Note-03:

 

• In max heap, every node contains greater or equal value element than all its descendants.
• In min heap, every node contains smaller value element that all its descendants.

 

PRACTICE PROBLEMS BASED ON HEAP DATA STRUCTURE-

 

Problems-

 

Consider a binary max-heap implemented using an array. Which one of the following array represents a binary max-heap? (GATE CS 2009)

1. 25, 14, 16, 13, 10, 8, 12
2. 25, 12, 16, 13, 10, 8, 14
3. 25, 14, 12, 13, 10, 8, 16
4. 25, 14, 13, 16, 10, 8, 12

 

Solutions-

 

Part-01: 25, 14, 16, 13, 10, 8, 12-

 

The given array representation may be converted into the following structure-

 

 

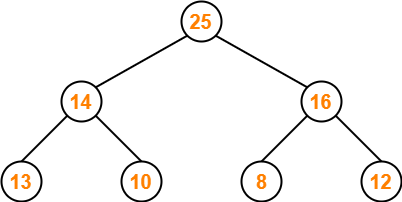
Clearly,

• It is a complete binary tree.
• Every node contains a greater value element than its child nodes.

 

Thus, the given array represents a max heap.

 

Part-02: 25, 12, 16, 13, 10, 8, 14-

 

The given array representation may be converted into the following structure-

 

 

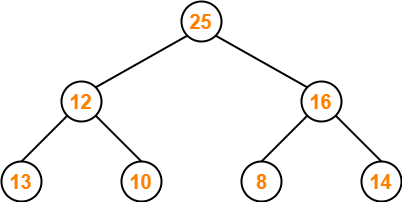
Clearly,

• It is a complete binary tree.
• Every node does not contain a greater value element than its child nodes. (Node 12)
• So, it is not a max heap.
• Every node does not contain a smaller value element than its child nodes.
• So, it is not a min heap.

 

Thus, the given array does not represents a heap.

 

Part-03: 25, 14, 12, 13, 10, 8, 16-

 

The given array representation may be converted into the following structure-

 

 

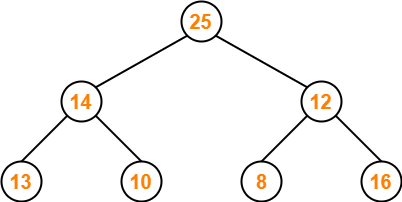
Clearly,

• It is a complete binary tree.
• Every node does not contain a greater value element than its child nodes. (Node 12)
• So, it is not a max heap.
• Every node does not contain a smaller value element than its child nodes.
• So, it is not a min heap.

 

Thus, the given array does not represents a heap.

 

Part-04: 25, 14, 13, 16, 10, 8, 12-

 

The given array representation may be converted into the following structure-

 

 

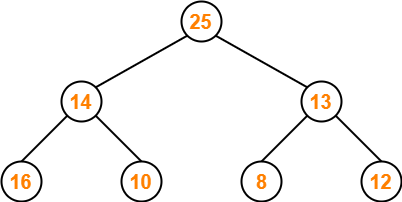
Clearly,

• It is a complete binary tree.
• Every node does not contain a greater value element than its child nodes. (Node 14)
• So, it is not a max heap.
• Every node does not contain a smaller value element than its child nodes.
• So, it is not a min heap.

 

Thus, the given array does not represents a heap.

 

To gain better understanding about Heap Data Structure,

Watch this Video Lecture

 

Next Article- Heap Operations

 

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.