Types of Graphs-
Before you go through this article, make sure that you have gone through the previous article on various Types of Graphs in Graph Theory.
We have discussed-
- A graph is a collection of vertices connected to each other through a set of edges.
- The study of graphs is known as Graph Theory.

In this article, we will discuss about Hamiltonian Graphs.
Hamiltonian Graph-
A Hamiltonian graph may be defined as-
| If there exists a closed walk in the connected graph that visits every vertex of the graph exactly once
(except starting vertex) without repeating the edges, then such a graph is called as a Hamiltonian graph. OR Any connected graph that contains a Hamiltonian circuit is called as a Hamiltonian Graph. |
Also Read- Euler Graph
Hamiltonian Graph Example-
The following graph is an example of a Hamiltonian graph-
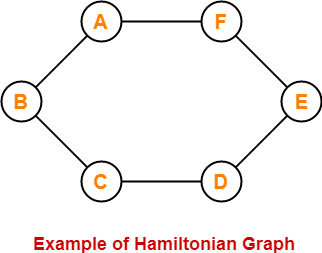
Here,
- This graph contains a closed walk ABCDEFA.
- It visits every vertex of the graph exactly once except starting vertex.
- The edges are not repeated during the walk.
- Therefore, it is a Hamiltonian graph.
Alternatively, there exists a Hamiltonian circuit ABCDEFA in the above graph, therefore it is a Hamiltonian graph.
Hamiltonian Path-
- If there exists a walk in the connected graph that visits every vertex of the graph exactly once without repeating the edges, then such a walk is called as a Hamiltonian path.
OR
- If there exists a Path in the connected graph that contains all the vertices of the graph, then such a path is called as a Hamiltonian path.
NOTEIn Hamiltonian path, all the edges may or may not be covered but edges must not repeat. |
Hamiltonian Path Examples-
Examples of Hamiltonian path are as follows-
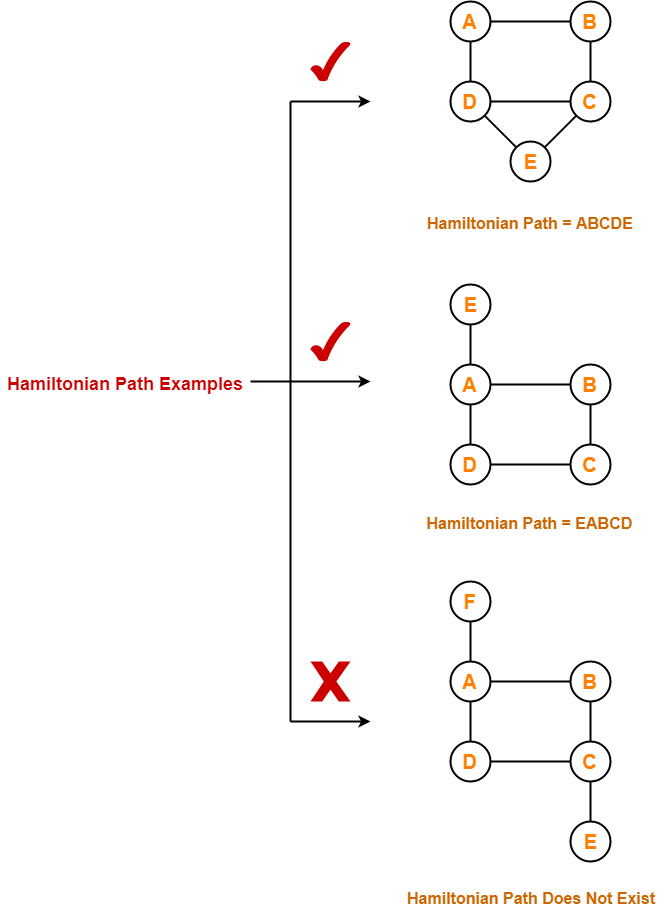
Hamiltonian Circuit-
Hamiltonian circuit is also known as Hamiltonian Cycle.
- If there exists a walk in the connected graph that visits every vertex of the graph exactly once (except starting vertex) without repeating the edges and returns to the starting vertex, then such a walk is called as a Hamiltonian circuit.
OR
- If there exists a Cycle in the connected graph that contains all the vertices of the graph, then that cycle is called as a Hamiltonian circuit.
OR
- A Hamiltonian path which starts and ends at the same vertex is called as a Hamiltonian circuit.
OR
- A closed Hamiltonian path is called as a Hamiltonian circuit.
Hamiltonian Circuit Examples-
Examples of Hamiltonian circuit are as follows-
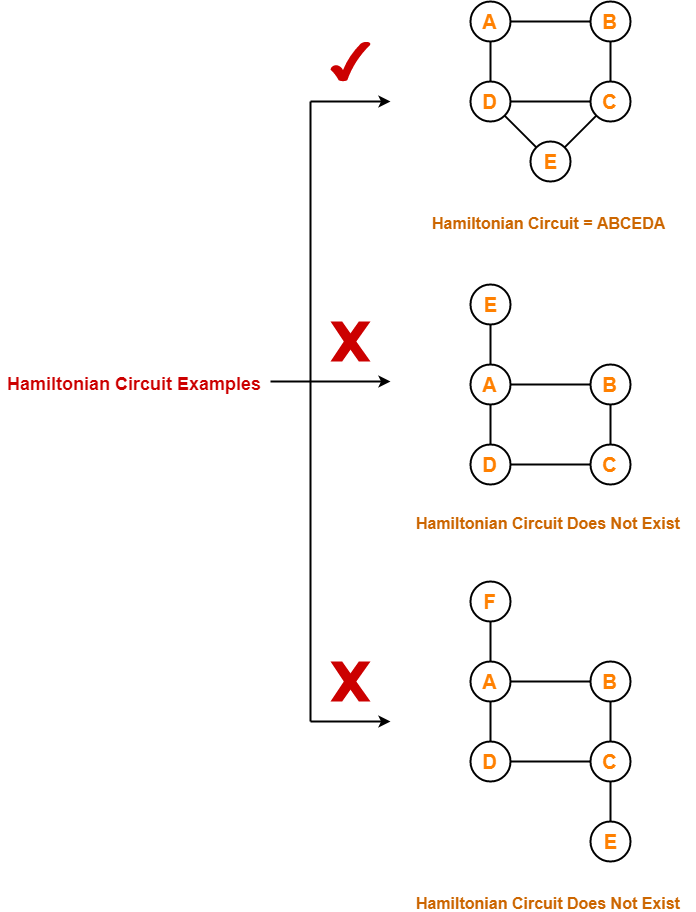
Important Notes-
- Any Hamiltonian circuit can be converted to a Hamiltonian path by removing one of its edges.
- Every graph that contains a Hamiltonian circuit also contains a Hamiltonian path but vice versa is not true.
- There may exist more than one Hamiltonian paths and Hamiltonian circuits in a graph.
Also Read- Planar Graph
PRACTICE PROBLEMS BASED ON HAMILTONIAN GRAPHS IN GRAPH THEORY-
Problems-
Which of the following is / are Hamiltonian graphs?
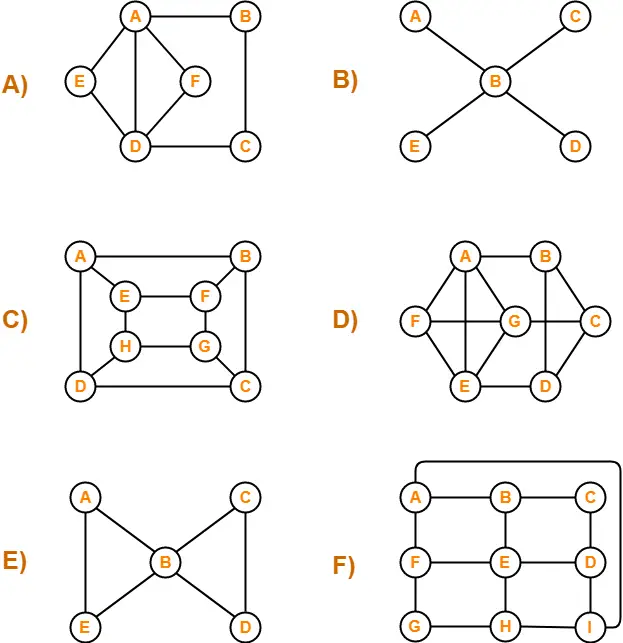
Solutions-
A)
The graph neither contains a Hamiltonian path nor it contains a Hamiltonian circuit.
Since graph does not contain a Hamiltonian circuit, therefore It is not a Hamiltonian Graph.
B)
The graph neither contains a Hamiltonian path nor it contains a Hamiltonian circuit.
Since graph does not contain a Hamiltonian circuit, therefore It is not a Hamiltonian Graph.
C)
The graph contains both a Hamiltonian path (ABCDHGFE) and a Hamiltonian circuit (ABCDHGFEA).
Since graph contains a Hamiltonian circuit, therefore It is a Hamiltonian Graph.
D)
The graph contains both a Hamiltonian path (ABCDEFG) and a Hamiltonian circuit (ABCDEFGA).
Since graph contains a Hamiltonian circuit, therefore It is a Hamiltonian Graph.
E)
The graph neither contains a Hamiltonian path nor it contains a Hamiltonian circuit.
Since graph does not contain a Hamiltonian circuit, therefore It is not a Hamiltonian Graph.
F)
The graph contains both a Hamiltonian path (ABCDEFGHI) and a Hamiltonian circuit (ABCDEFGHIA)
Since graph contains a Hamiltonian circuit, therefore It is a Hamiltonian Graph.
To gain better understanding about Hamiltonian Graphs in Graph Theory,
Next Article- Bipartite Graph
Get more notes and other study material of Graph Theory.
Watch video lectures by visiting our YouTube channel LearnVidFun.