Types of Graphs-
Before you go through this article, make sure that you have gone through the previous article on various Types of Graphs in Graph Theory.
We have discussed-
- A graph is a collection of vertices connected to each other through a set of edges.
- The study of graphs is known as Graph Theory.

In this article, we will discuss about Planar Graphs.
Planar Graph-
A planar graph may be defined as-
| In graph theory,
Planar graph is a graph that can be drawn in a plane such that none of its edges cross each other. |
Planar Graph Example-
The following graph is an example of a planar graph-
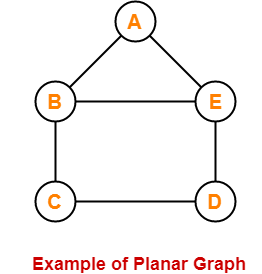
Here,
- In this graph, no two edges cross each other.
- Therefore, it is a planar graph.
Regions of Plane-
The planar representation of the graph splits the plane into connected areas called as Regions of the plane.
Each region has some degree associated with it given as-
- Degree of Interior region = Number of edges enclosing that region
- Degree of Exterior region = Number of edges exposed to that region
Example-
Consider the following planar graph-
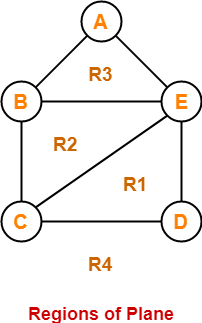
Here, this planar graph splits the plane into 4 regions- R1, R2, R3 and R4 where-
- Degree (R1) = 3
- Degree (R2) = 3
- Degree (R3) = 3
- Degree (R4) = 5
Planar Graph Chromatic Number-
- Chromatic Number of any planar graph is always less than or equal to 4.
- Thus, any planar graph always requires maximum 4 colors for coloring its vertices.
Planar Graph Properties-
Property-01:
In any planar graph, Sum of degrees of all the vertices = 2 x Total number of edges in the graph
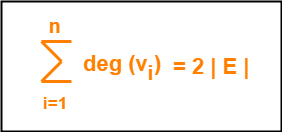
Property-02:
In any planar graph, Sum of degrees of all the regions = 2 x Total number of edges in the graph
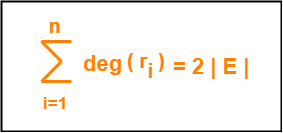
Special Cases
Case-01:
In any planar graph, if degree of each region is K, then-
Case-02:
In any planar graph, if degree of each region is at least K (>=K), then-
Case-03:
In any planar graph, if degree of each region is at most K (<=K), then-
|
Property-03:
If G is a connected planar simple graph with ‘e’ edges, ‘v’ vertices and ‘r’ number of regions in the planar representation of G, then-
| r = e – v + 2 |
This is known as Euler’s Formula.
It remains same in all the planar representations of the graph.
Property-04:
If G is a planar graph with k components, then-
| r = e – v + (k + 1) |
Also Read- Bipartite Graph
PRACTICE PROBLEMS BASED ON PLANAR GRAPH IN GRAPH THEORY-
Problem-01:
Let G be a connected planar simple graph with 25 vertices and 60 edges. Find the number of regions in G.
Solution-
Given-
- Number of vertices (v) = 25
- Number of edges (e) = 60
By Euler’s formula, we know r = e – v + 2.
Substituting the values, we get-
Number of regions (r)
= 60 – 25 + 2
= 37
Thus, Total number of regions in G = 37.
Problem-02:
Let G be a planar graph with 10 vertices, 3 components and 9 edges. Find the number of regions in G.
Solution-
Given-
- Number of vertices (v) = 10
- Number of edges (e) = 9
- Number of components (k) = 3
By Euler’s formula, we know r = e – v + (k+1).
Substituting the values, we get-
Number of regions (r)
= 9 – 10 + (3+1)
= -1 + 4
= 3
Thus, Total number of regions in G = 3.
Problem-03:
Let G be a connected planar simple graph with 20 vertices and degree of each vertex is 3. Find the number of regions in G.
Solution-
Given-
- Number of vertices (v) = 20
- Degree of each vertex (d) = 3
Calculating Total Number Of Edges (e)-
By sum of degrees of vertices theorem, we have-
Sum of degrees of all the vertices = 2 x Total number of edges
Number of vertices x Degree of each vertex = 2 x Total number of edges
20 x 3 = 2 x e
∴ e = 30
Thus, Total number of edges in G = 30.
Calculating Total Number Of Regions (r)-
By Euler’s formula, we know r = e – v + 2.
Substituting the values, we get-
Number of regions (r)
= 30 – 20 + 2
= 12
Thus, Total number of regions in G = 12.
Problem-04:
Let G be a connected planar simple graph with 35 regions, degree of each region is 6. Find the number of vertices in G.
Solution-
Given-
- Number of regions (n) = 35
- Degree of each region (d) = 6
Calculating Total Number Of Edges (e)-
By sum of degrees of regions theorem, we have-
Sum of degrees of all the regions = 2 x Total number of edges
Number of regions x Degree of each region = 2 x Total number of edges
35 x 6 = 2 x e
∴ e = 105
Thus, Total number of edges in G = 105.
Calculating Total Number Of Vertices (v)-
By Euler’s formula, we know r = e – v + 2.
Substituting the values, we get-
35 = 105 – v + 2
∴ v = 72
Thus, Total number of vertices in G = 72.
Problem-05:
Let G be a connected planar graph with 12 vertices, 30 edges and degree of each region is k. Find the value of k.
Solution-
Given-
- Number of vertices (v) = 12
- Number of edges (e) = 30
- Degree of each region (d) = k
Calculating Total Number Of Regions (r)-
By Euler’s formula, we know r = e – v + 2.
Substituting the values, we get-
Number of regions (r)
= 30 – 12 + 2
= 20
Thus, Total number of regions in G = 20.
Calculating Value Of k-
By sum of degrees of regions theorem, we have-
Sum of degrees of all the regions = 2 x Total number of edges
Number of regions x Degree of each region = 2 x Total number of edges
20 x k = 2 x 30
∴ k = 3
Thus, Degree of each region in G = 3.
Problem-06:
What is the maximum number of regions possible in a simple planar graph with 10 edges?
Solution-
In a simple planar graph, degree of each region is >= 3.
So, we have 3 x |R| <= 2 x |E|.
Substituting the value |E| = 10, we get-
3 x |R| <= 2 x 10
|R| <= 6.67
|R| <= 6
Thus, Maximum number of regions in G = 6.
Problem-07:
What is the minimum number of edges necessary in a simple planar graph with 15 regions?
Solution-
In a simple planar graph, degree of each region is >= 3.
So, we have 3 x |R| <= 2 x |E|.
Substituting the value |R| = 15, we get-
3 x 15 <= 2 x |E|
|E| >= 22.5
|E| >= 23
Thus, Minimum number of edges required in G = 23.
To gain better understanding about Planar Graphs in Graph Theory,
Next Article- Euler Graph
Get more notes and other study material of Graph Theory.
Watch video lectures by visiting our YouTube channel LearnVidFun.

