Types of Graphs in Graph Theory

Graphs-

 

• A graph is a collection of vertices connected to each other through a set of edges.
• The study of graphs is known as Graph Theory.

 

Formal Definition Formally, A graph is defined as an ordered pair of a set of vertices and a set of edges. G = (V, E) Here, V is the set of vertices and E is the set of edges connecting the vertices.

 

Example-

 

 

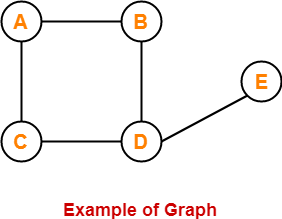
In this graph,

V = { A , B , C , D , E }

E = { AB , AC , BD , CD , DE }

 

Types of Graphs-

 

Various important types of graphs in graph theory are-

 

 

1. Null Graph
2. Trivial Graph
3. Non-directed Graph
4. Directed Graph
5. Connected Graph
6. Disconnected Graph
7. Regular Graph
8. Complete Graph
9. Cycle Graph
10. Cyclic Graph
11. Acyclic Graph
12. Finite Graph
13. Infinite Graph
14. Bipartite Graph
15. Planar Graph
16. Simple Graph
17. Multi Graph
18. Pseudo Graph
19. Euler Graph
20. Hamiltonian Graph

 

1. Null Graph-

 

• A graph whose edge set is empty is called as a null graph.
• In  other words, a null graph does not contain any edges in it.

 

Example-

 

 

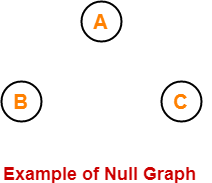
Here,

• This graph consists only of the vertices and there are no edges in it.
• Since the edge set is empty, therefore it is a null graph.

 

2. Trivial Graph-

 

• A graph having only one vertex in it is called as a trivial graph.
• It is the smallest possible graph.

 

Example-

 

 

Here,

• This graph consists of only one vertex and there are no edges in it.
• Since only one vertex is present, therefore it is a trivial graph.

 

3. Non-Directed Graph-

 

• A graph in which all the edges are undirected is called as a non-directed graph.
• In other words, edges of an undirected graph do not contain any direction.

 

Example-

 

 

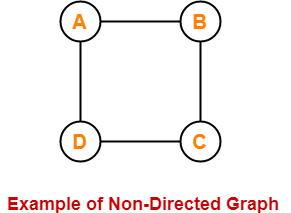
Here,

• This graph consists of four vertices and four undirected edges.
• Since all the edges are undirected, therefore it is a non-directed graph.

 

4. Directed Graph-

 

• A graph in which all the edges are directed is called as a directed graph.
• In other words, all the edges of a directed graph contain some direction.
• Directed graphs are also called as digraphs.

 

Example-

 

 

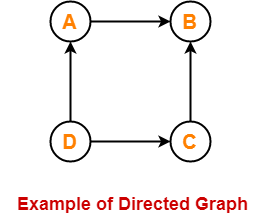
Here,

• This graph consists of four vertices and four directed edges.
• Since all the edges are directed, therefore it is a directed graph.

 

5. Connected Graph-

 

• A graph in which we can visit from any one vertex to any other vertex is called as a connected graph.
• In connected graph, at least one path exists between every pair of vertices.

 

Example-

 

 

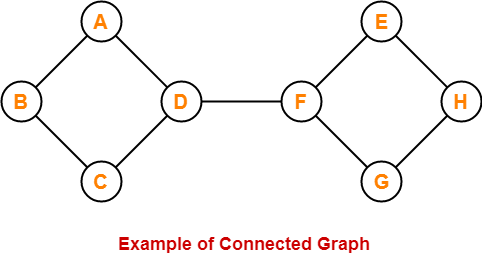
Here,

• In this graph, we can visit from any one vertex to any other vertex.
• There exists at least one path between every pair of vertices.
• Therefore, it is a connected graph.

 

6. Disconnected Graph-

 

• A graph in which there does not exist any path between at least one pair of vertices is called as a disconnected graph.

 

Example-

 

 

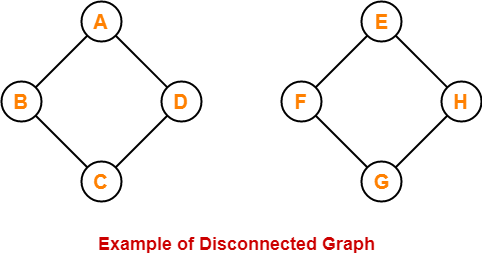
Here,

• This graph consists of two independent components which are disconnected.
• It is not possible to visit from the vertices of one component to the vertices of other component.
• Therefore, it is a disconnected graph.

 

7. Regular Graph-

 

• A graph in which degree of all the vertices is same is called as a regular graph.
• If all the vertices in a graph are of degree ‘k’, then it is called as a “k-regular graph“.

 

Examples-

 

 

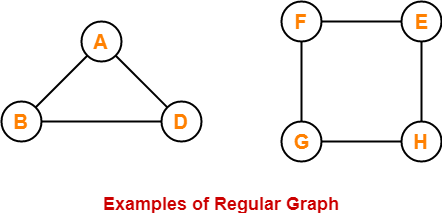
In these graphs,

• All the vertices have degree-2.
• Therefore, they are 2-Regular graphs.

 

8. Complete Graph-

 

• A graph in which exactly one edge is present between every pair of vertices is called as a complete graph.
• A complete graph of ‘n’ vertices contains exactly ⁿC₂ edges.
• A complete graph of ‘n’ vertices is represented as K_n.

 

Examples-

 

 

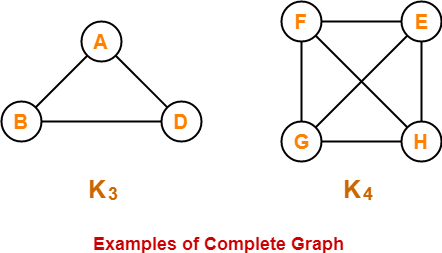
In these graphs,

• Each vertex is connected with all the remaining vertices through exactly one edge.
• Therefore, they are complete graphs.

 

9. Cycle Graph-

 

• A simple graph of ‘n’ vertices (n>=3) and n edges forming a cycle of length ‘n’ is called as a cycle graph.
• In a cycle graph, all the vertices are of degree 2.

 

Examples-

 

 

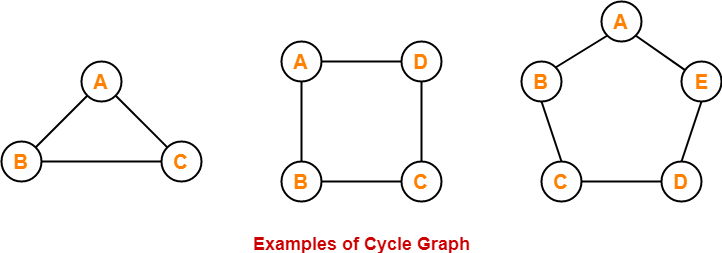
In these graphs,

• Each vertex is having degree 2.
• Therefore, they are cycle graphs.

 

10. Cyclic Graph-

 

• A graph containing at least one cycle in it is called as a cyclic graph.

 

Example-

 

 

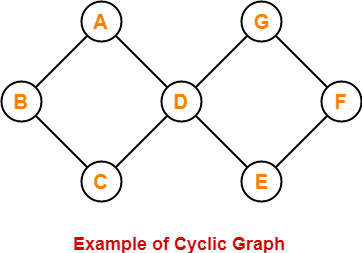
Here,

• This graph contains two cycles in it.
• Therefore, it is a cyclic graph.

 

11. Acyclic Graph-

 

• A graph not containing any cycle in it is called as an acyclic graph.

 

Example-

 

 

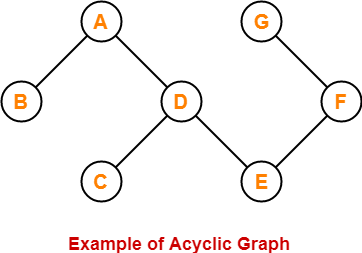
Here,

• This graph do not contain any cycle in it.
• Therefore, it is an acyclic graph.

 

12. Finite Graph-

 

• A graph consisting of finite number of vertices and edges is called as a finite graph.

 

Example-

 

 

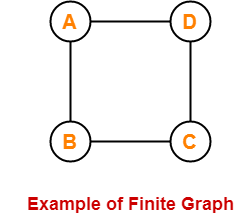
Here,

• This graph consists of finite number of vertices and edges.
• Therefore, it is a finite graph.

 

13. Infinite Graph-

 

• A graph consisting of infinite number of vertices and edges is called as an infinite graph.

 

Example-

 

 

Here,

• This graph consists of infinite number of vertices and edges.
• Therefore, it is an infinite graph.

 

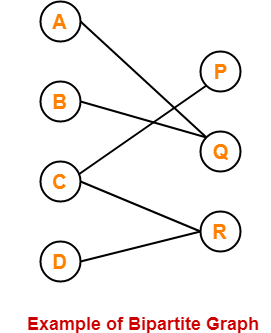
14. Bipartite Graph-

 

A bipartite graph is a graph where-

• Vertices can be divided into two sets X and Y.
• The vertices of set X only join with the vertices of set Y.
• None of the vertices belonging to the same set join each other.

 

Example-

 

 

Read More- Bipartite Graphs

 

15. Planar Graph-

 

• A planar graph is a graph that we can draw in a plane such that no two edges of it cross each other.

 

Example-

 

 

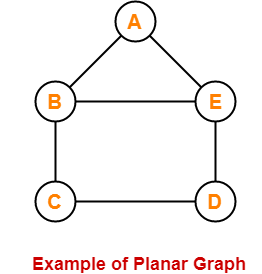
Here,

• This graph can be drawn in a plane without crossing any edges.
• Therefore, it is a planar graph.

 

Read More- Planar Graphs

 

16. Simple Graph-

 

• A graph having no self loops and no parallel edges in it is called as a simple graph.

 

Example-

 

 

Here,

• This graph consists of three vertices and three edges.
• There are neither self loops nor parallel edges.
• Therefore, it is a simple graph.

 

17. Multi Graph-

 

• A graph having no self loops but having parallel edge(s) in it is called as a multi graph.

 

Example-

 

 

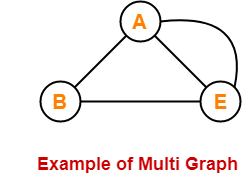
Here,

• This graph consists of three vertices and four edges out of which one edge is a parallel edge.
• There are no self loops but a parallel edge is present.
• Therefore, it is a multi graph.

 

18. Pseudo Graph-

 

• A graph having no parallel edges but having self loop(s) in it is called as a pseudo graph.

 

Example-

 

 

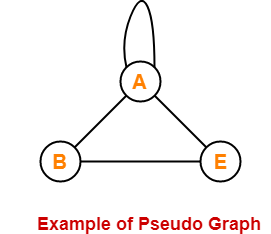
Here,

• This graph consists of three vertices and four edges out of which one edge is a self loop.
• There are no parallel edges but a self loop is present.
• Therefore, it is a pseudo graph.

 

19. Euler Graph-

 

• Euler Graph is a connected graph in which all the vertices are even degree.

 

Example-

 

 

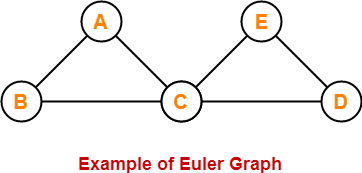
Here,

• This graph is a connected graph.
• The degree of all the vertices is even.
• Therefore, it is an Euler graph.

 

Read More- Euler Graphs

 

20. Hamiltonian Graph-

 

• If there exists a closed walk in the connected graph that visits every vertex of the graph exactly once (except starting vertex) without repeating the edges, then such a graph is called as a Hamiltonian graph.

 

Example-

 

 

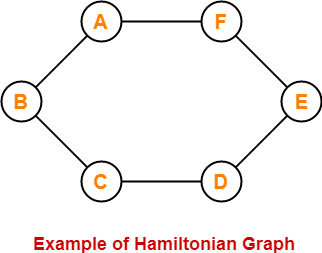
Here,

• This graph contains a closed walk ABCDEFG that visits all the vertices (except starting vertex) exactly once.
• All the vertices are visited without repeating the edges.
• Therefore, it is a Hamiltonian Graph.

 

Read More- Hamiltonian Graphs

 

Important Points-

 

• Edge set of a graph can be empty but vertex set of a graph can not be empty.
• Every polygon is a 2-Regular Graph.
• Every complete graph of ‘n’ vertices is a (n-1)-regular graph.
• Every regular graph need not be a complete graph.

 

Remember-

 

The following table is useful to remember different types of graphs-

 

	Self-Loop(s)	Parallel Edge(s)
Graph	Yes	Yes
Simple Graph	No	No
Multi Graph	No	Yes
Pseudo Graph	Yes	No

 

Applications of Graph Theory-

 

Graph theory has its applications in diverse fields of engineering-

 

1. Electrical Engineering-

 

• The concepts of graph theory are used extensively in designing circuit connections.
• The types or organization of connections are named as topologies.
• Some examples for topologies are star, bridge, series and parallel topologies.

 

2. Computer Science-

 

Graph theory is used for the study of algorithms such as-

• Kruskal’s Algorithm
• Prim’s Algorithm
• Dijkstra’s Algorithm

 

3. Computer Network-

 

The relationships among interconnected computers in the network follows the principles of graph theory.

 

4. Science-

 

Following structures are represented by graphs-

• Molecular structure of a substance
• Chemical structure of a substance
• DNA structure of an organism etc

 

5. Linguistics-

 

The parsing tree of a language and grammar of a language uses graphs.

 

6. Other Applications-

 

• Routes between the cities are represented using graphs.
• Hierarchical ordered information such as family tree are represented using special types of graphs called trees.

 

Next Article- Planar Graph

 

Get more notes and other study material of Graph Theory.

Watch video lectures by visiting our YouTube channel LearnVidFun.