Category: Digital Design

Boolean Algebra & Its Use in Computer Science

Digital Design

What Is Boolean Algebra And Why Is It Used in Computer Science?

 

George Boole, an English mathematician tried to find a way to express and simplify difficult algebraic algorithms and built a system called Boolean algebra.

 

What Is Boolean Algebra?

 

Boolean algebra is a mathematical system that consists of symbols that are used to understand the relativity between two contents.

The two logical variables are-

  • TRUE
  • FALSE

True is represented by 1 and false by 0.

Logic circuits are being designed by the use of Boolean Algebra. It is simple yet powerful part of Algebra that can be used for performing simple to complex analysis.

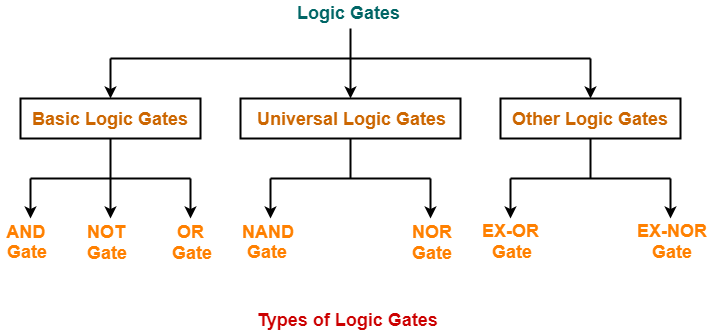
The following five types of operations can be performed with Boolean algebra-

  • NOT
  • AND
  • OR
  • NAND
  • NOR

 

NOT-

 

NOT gives the reverse outcome of the input that’s being made. For example, if you have given 1 as an input, NOT will generate the opposite as an output which is 0 and vice-versa. So, in total you can have two possible outcomes.

 

Input Output
0 1
1 0

NOT Table

 

AND-

 

With AND, you have to make two digits input and the output depends on them.

If you have given both 1 as input in AND operation, you will get 1 as an output otherwise the output will be zero.

 

Input 1 Input 2 Output
0 0 0
0 1 0
1 0 0
1 1 1

AND Table

 

OR-

 

With OR, you have to make two digits input and the output depends on them.

If one of the values given to OR operation is 1, then the output would be 1 otherwise 0.

 

Input-1 Input-2 Output
0 0 0
0 1 1
1 0 1
1 1 1

OR Table

 

NAND-

 

When you combine AND and NOT, the output is NAND. Together they form a cascade. If both the inputs are 1, then the output will be 0 otherwise all combinations will result in 1.

 

Input-1 Input-2 Output
0 0 1
0 1 1
1 0 1
1 1 0

NAND Table

 

NOR-

 

The combination of NOT and OR will result in NOR. It reverses the output of OR. When both the inputs are 0, that’s only way the output comes is 1. Rest of the inputs gets 0 as output.

 

Input-1 Input-2 Output
0 0 1
0 1 0
1 0 0
1 1 0

NOR Table

 

Basic Boolean Laws-

 

Boolean algebra comes with the set number of laws in order to simplify boolean expressions properly.

Basic Boolean Laws are as follows:

 

1. Idempotent Law-

 

A * A = A             (A variable AND with itself is always equal to the variable)

A + A = A            (A variable OR with itself is always equal to the variable)

 

2. Associative Law-

 

You can re-group the variables by removing the brackets-

 

(A * B) * C = A * (B * C)

(A + B) + C = A + (B + C)

 

3. Commutative Law-

 

Application order change doesn’t matter. It’s same one way or the other-

 

A * B = B * A

A + B = B + A

 

4. Distributive Law-

 

This law allows you to multiply or factor out the variables-

 

A * (B + C) = A * B + A * C

A + (B * C) = (A + B) * (A + C)

 

5. Identity Law-

 

A * 0 = 0     A * 1 = A          (A variable AND with 1 is always equal to the variable)

A + 1 = 1     A + 0 = A         (A variable OR with 0 is always equal to the variable)

 

6. Complement Law-

 

A * ~A = 0           (A variable AND with its complement is always equal to 0)

A + ~A = 1          (A variable OR with its complement is always equal to 1)

 

7. Involution Law-

 

~(~A) = A

 

8. DeMorgan’s Law-

 

~(A * B) = ~A + ~B

Two separate terms NAND together is the same as the two terms Complemented and OR

 

~(A + B) = ~A * ~B

Two separate terms NOR together is the same as the two terms Complemented and AND

 

9. Absorption-

 

In this law, like terms gets absorbed in order to simplify a complicated expression-

A + (A * B) = A

A * (A + B) = A

 

Each law is described by two parts that are duals of each other.

The duality Principle is Interchanging the + (OR) and * (AND) operations of the expression or interchanging the 0 and 1 variables of the expression and not changing the form of the variables.

 

Not everyone has the mathematical mind and simplifying such complex expressions can be very difficult for them. One needs help in such matters from time to time.

 

Boolean Algebra Calculator-

 

In order to make your life easy, Boolean Calculator is available online that can help you simply any boolean expression. You can easily find the truth table with its help.

Boolean Algebra Calculator is very ease to use. It can simplify any expression in no time. All you have to do is add an expression and press PARSE and that’s it.

The complicated Algebraic expression gets simple with a click and you get the result that you can use with what ever task you are performing.

 

Uses Of Boolean Algebra In Computer Science-

 

Boolean Algebra has wide range of usage in computer science world. A lot of programming is done with the help of Boolean Algebra. It consist of two expressions and their comparison.

 

For Example-

 

You will always get a true result 5 < 8 as 5 is always less than 8.

In x<6, you will only get the true result when x is a number that is less than 6 but a false result if x is a number that is equal to or greater than 6.

A<B is only true when A is a variable that is less than variable B. For programming purposes, other data types can also be used.

Overall, Boolean algebra has been very helpful in our lives.

 

K Maps | karnaugh Maps | Solved Examples

Digital Design

Minimization Of Boolean Expressions-

 

There are following two methods of minimizing or reducing the boolean expressions-

 

 

  1. By using laws of Boolean Algebra
  2. By using Karnaugh Maps also called as K Maps

 

In this article, we will discuss about Karnaugh Maps or K Maps.

 

Karnaugh Map-

 

The Karnaugh Map also called as K Map is a graphical representation

that provides a systematic method for simplifying the boolean expressions.

 

For a boolean expression consisting of n-variables, number of cells required in K Map = 2n cells.

 

Two Variable K Map-

 

  • Two variable K Map is drawn for a boolean expression consisting of two variables.
  • The number of cells present in two variable K Map = 22 = 4 cells.
  • So, for a boolean function consisting of two variables, we draw a 2 x 2 K Map.

 

Two variable K Map may be represented as-

 

 

Here, A and B are the two variables of the given boolean function.

 

Three Variable K Map-

 

  • Three variable K Map is drawn for a boolean expression consisting of three variables.
  • The number of cells present in three variable K Map = 23 = 8 cells.
  • So, for a boolean function consisting of three variables, we draw a 2 x 4 K Map.

 

Three variable K Map may be represented as-

 

 

Here, A, B and C are the three variables of the given boolean function.

 

Four Variable K Map-

 

  • Four variable K Map is drawn for a boolean expression consisting of four variables.
  • The number of cells present in four variable K Map = 24 = 16 cells.
  • So, for a boolean function consisting of four variables, we draw a 4 x 4 K Map.

 

Four variable K Map may be represented as-

 

 

Here, A, B, C and D are the four variables of the given boolean function.

 

Karnaugh Map Simplification Rules-

 

To minimize the given boolean function,

  • We draw a K Map according to the number of variables it contains.
  • We fill the K Map with 0’s and 1’s according to its function.
  • Then, we minimize the function in accordance with the following rules.

 

Rule-01:

 

  • We can either group 0’s with 0’s or 1’s with 1’s but we can not group 0’s and 1’s together.
  • X representing don’t care can be grouped with 0’s as well as 1’s.

 

NOTE

There is no need of separately grouping X’s i.e. they can be ignored if all 0’s and 1’s are already grouped.

 

Rule-02:

 

  • Groups may overlap each other.

 

Rule-03:

 

  • We can only create a group whose number of cells can be represented in the power of 2.
  • In other words, a group can only contain 2n i.e. 1, 2, 4, 8, 16 and so on number of cells.

 

Example-

 

 

Rule-04:

 

  • Groups can be only either horizontal or vertical.
  • We can not create groups of diagonal or any other shape.

 

 

Rule-05:

 

  • Each group should be as large as possible.

 

Example-

 

 

Rule-06:

 

  • Opposite grouping and corner grouping are allowed.
  • The example of opposite grouping is shown illustrated in Rule-05.
  • The example of corner grouping is shown below.

 

Example-

 

 

Rule-07:

 

  • There should be as few groups as possible.

 

PROBLEMS BASED ON KARNAUGH MAP-

 

Problem-01:

 

Minimize the following boolean function-

F(A, B, C, D) = Σm(0, 1, 2, 5, 7, 8, 9, 10, 13, 15)

 

Solution-

 

  • Since the given boolean expression has 4 variables, so we draw a 4 x 4 K Map.
  • We fill the cells of K Map in accordance with the given boolean function.
  • Then, we form the groups in accordance with the above rules.

 

Then, we have-

 

 

Now,

F(A, B, C, D)

= (A’B + AB)(C’D + CD) + (A’B’ + A’B + AB + AB’)C’D + (A’B’ + AB’)(C’D’ + CD’)

= BD + C’D + B’D’

 

Thus, minimized boolean expression is-

F(A, B, C, D) = BD + C’D + B’D’

 

Problem-02:

 

Minimize the following boolean function-

F(A, B, C, D) = Σm(0, 1, 3, 5, 7, 8, 9, 11, 13, 15)

 

Solution-

 

  • Since the given boolean expression has 4 variables, so we draw a 4 x 4 K Map.
  • We fill the cells of K Map in accordance with the given boolean function.
  • Then, we form the groups in accordance with the above rules.

 

Then, we have-

 

 

Now,

F(A, B, C, D)

= (A’B’ + A’B + AB + AB’)(C’D + CD) + (A’B’ + AB’)(C’D’ + C’D)

= D + B’C’

 

Thus, minimized boolean expression is-

F(A, B, C, D) = B’C’ + D

 

Problem-03:

 

Minimize the following boolean function-

F(A, B, C, D) = Σm(1, 3, 4, 6, 8, 9, 11, 13, 15) + Σd(0, 2, 14)

 

Solution-

 

  • Since the given boolean expression has 4 variables, so we draw a 4 x 4 K Map.
  • We fill the cells of K Map in accordance with the given boolean function.
  • Then, we form the groups in accordance with the above rules.

 

Then, we have-

 

 

Now,

F(A, B, C, D)

= (AB + AB’)(C’D + CD) + (A’B’ + AB’)(C’D + CD) + (A’B’ + AB’)(C’D’ + C’D) + (A’B’ + A’B)(C’D’ + CD’)

= AD + B’D + B’C’ + A’D’

 

Thus, minimized boolean expression is-

F(A, B, C, D) = AD + B’D + B’C’ + A’D’

 

Problem-04:

 

Minimize the following boolean function-

F(A, B, C) = Σm(0, 1, 6, 7) + Σd(3, 5)

 

Solution-

 

  • Since the given boolean expression has 3 variables, so we draw a 2 x 4 K Map.
  • We fill the cells of K Map in accordance with the given boolean function.
  • Then, we form the groups in accordance with the above rules.

 

Then, we have-

 

 

Now,

F(A, B, C)

= A'(B’C’ + B’C) + A(BC + BC’)

= A’B’ + AB

 

Thus, minimized boolean expression is-

F(A, B, C) = AB + A’B’

 

NOTE-

 

  • It may be noted that there is no need of considering the quad group.
  • This is because even if we consider that group, we will have to consider the other two duets.
  • So, there is no use of considering that quad group.

 

Problem-05:

 

Minimize the following boolean function-

F(A, B, C) = Σm(1, 2, 5, 7) + Σd(0, 4, 6)

 

Solution-

 

  • Since the given boolean expression has 3 variables, so we draw a 2 x 4 K Map.
  • We fill the cells of K Map in accordance with the given boolean function.
  • Then, we form the groups in accordance with the above rules.

 

Then, we have-

 

 

Now,

F(A, B, C)

= (A + A’)(B’C’ + B’C) + A(B’C’ + B’C + BC + BC’) + (A + A’)(B’C’ + BC’)

= B’ + A + C’

 

Thus, minimized boolean expression is-

F(A, B, C) = A + B’ + C’

 

Problem-06:

 

Minimize the following boolean function-

F(A, B, C) = Σm(0, 1, 6, 7) + Σd(3, 4, 5)

 

Solution-

 

  • Since the given boolean expression has 3 variables, so we draw a 2 x 4 K Map.
  • We fill the cells of K Map in accordance with the given boolean function.
  • Then, we form the groups in accordance with the above rules.

 

Then, we have-

 

 

Now,

F(A, B, C)

= (A + A’)(B’C’ + B’C) + A(B’C’ + B’C + BC + BC’)

= B’ + A

 

Thus, minimized boolean expression is-

F(A, B, C) = A + B’

 

Problem-07:

 

Minimize the following boolean function-

F(A, B, C, D) = Σm(0, 2, 8, 10, 14) + Σd(5, 15)

 

Solution-

 

  • Since the given boolean expression has 4 variables, so we draw a 4 x 4 K Map.
  • We fill the cells of K Map in accordance with the given boolean function.
  • Then, we form the groups in accordance with the above rules.

 

Then, we have-

 

 

Now,

F(A, B, C, D)

= (AB + AB’)CD’ + (A’B’ + AB’)(C’D’ + CD’)

= ACD’ + B’D’

 

Thus, minimized boolean expression is-

F(A, B, C, D) = ACD’ + B’D’

 

Problem-08:

 

Minimize the following boolean function-

F(A, B, C, D) = Σm(3, 4, 5, 7, 9, 13, 14, 15)

 

Solution-

 

  • Since the given boolean expression has 4 variables, so we draw a 4 x 4 K Map.
  • We fill the cells of K Map in accordance with the given boolean function.
  • Then, we form the groups in accordance with the above rules.

 

Then, we have-

 

 

Now,

F(A, B, C, D)

= A’B(C’D’ + C’D) + (A’B’ + A’B)(CD) + (AB + AB’)(C’D) + AB(CD + CD’)

= A’BC’ + A’CD + AC’D + ABC

 

Thus, minimized boolean expression is-

F(A, B, C, D) = A’BC’ + A’CD + AC’D + ABC

 

It is important to note that we are not considering the quad group because we have to consider the duets anyhow.

 

Problem-09:

 

Consider the following boolean function-

F(W, X, Y, Z) = Σm(1, 3, 4, 6, 9, 11, 12, 14)

 

This function is independent ________ number of variables. Fill in the blank.

 

Solution-

 

  • Since the given boolean expression has 4 variables, so we draw a 4 x 4 K Map.
  • We fill the cells of K Map in accordance with the given boolean function.
  • Then, we form the groups in accordance with the above rules.

 

Then, we have-

 

 

Now,

F(W, X, Y, Z)

= (W’X + WX)(Y’Z’ + YZ’) + (W’X’ + WX’)(Y’Z + YZ)

= XZ’ + X’Z

= X ⊕ Z

 

Thus, minimized boolean expression is-

F(W, X, Y, Z) = X ⊕ Z

 

Clearly, the given boolean function depends on only two variables X and Z.

Hence, it is independent of other two variables W and Y.

 

Next Article- Neutral Functions

 

Get more notes and other study material of Digital Design.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Carry Look Ahead Adder | 4-bit Carry Look Ahead Adder

Digital Design

Ripple Carry Adder-

 

Before you go through this article, make sure that you have gone through the previous article on Ripple Carry Adder.

 

In Ripple Carry Adder,

  • Each full adder has to wait for its carry-in from its previous stage full adder.
  • Thus, nth full adder has to wait until all (n-1) full adders have completed their operations.
  • This causes a delay and makes ripple carry adder extremely slow.
  • The situation becomes worst when the value of n becomes very large.
  • To overcome this disadvantage, Carry Look Ahead Adder comes into play.

 

 

In this article, we will discuss about Carry Look Ahead Adder.

 

Carry Look Ahead Adder-

 

  • Carry Look Ahead Adder is an improved version of the ripple carry adder.
  • It generates the carry-in of each full adder simultaneously without causing any delay.
  • The time complexity of carry look ahead adder = Θ (logn).

 

Logic Diagram-

 

The logic diagram for carry look ahead adder is as shown below-

 

 

Carry Look Ahead Adder Working-

 

The working of carry look ahead adder is based on the principle-

The carry-in of any stage full adder is independent of the carry bits generated during intermediate stages.

 

The carry-in of any stage full adder depends only on the following two parameters-

  • Bits being added in the previous stages
  • Carry-in provided in the beginning

 

Now,

  • The above two parameters are always known from the beginning.
  • So, the carry-in of any stage full adder can be evaluated at any instant of time.
  • Thus, any full adder need not wait until its carry-in is generated by its previous stage full adder.

 

Also Read- Full Adder Working

 

4-Bit Carry Look Ahead Adder-

 

Consider two 4-bit binary numbers A3A2A1A0 and B3B2B1B0 are to be added.

Mathematically, the two numbers will be added as-

 

 

From here, we have-

C1 = C0 (A0 ⊕ B0) + A0B0

C2 = C1 (A1 ⊕ B1) + A1B1

C3 = C2 (A2 ⊕ B2) + A2B2

C4 = C3 (A3 ⊕ B3) + A3B3

 

For simplicity, Let-

  • Gi = AiBi where G is called carry generator
  • Pi = Ai ⊕ Bi where P is called carry propagator

 

Then, re-writing the above equations, we have-

C1 = C0P0 + G0 ………….. (1)

C2 = C1P1 + G1 ………….. (2)

C3 = C2P2 + G2 ………….. (3)

C4 = C3P3 + G3 ………….. (4)

 

Now,

  • Clearly, C1, C2 and C3 are intermediate carry bits.
  • So, let’s remove C1, C2 and C3 from RHS of every equation.
  • Substituting (1) in (2), we get C2 in terms of C0.
  • Then, substituting (2) in (3), we get C3 in terms of C0 and so on.

 

Finally, we have the following equations-

  • C1 = C0P0 + G0 
  • C2 = C0P0P1 + G0P1 + G1
  • C3 = C0P0P1P2 + G0P1P2 + G1P2 + G2
  • C4 =C0P0P1P2P3 + G0P1P2P3 + G1P2P3 + G2P3 + G3

 

These equations are important to remember.

 

These equations show that the carry-in of any stage full adder depends only on-

  • Bits being added in the previous stages
  • Carry bit which was provided in the beginning

 

Trick To Memorize Above Equations-

 

As an example, let us consider the equation for generating carry bit C2.

There are three possible reasons for generation of C2 as depicted in the following picture-

 

 

In the similar manner, we can write other equations as well very easily.

 

Implementation Of Carry Generator Circuits-

 

The above carry generator circuits are usually implemented as-

  • Two level combinational circuits.
  • Using AND and OR gates where gates are assumed to have any number of inputs.

 

Implementation Of C1–

 

  • The carry generator circuit for C1 is implemented as shown below.
  • It requires 1 AND gate and 1 OR gate.

 

C1 = C0P0 + G0

 

Implementation Of C2–

 

  • The carry generator circuit for C2 is implemented as shown below.
  • It requires 2 AND gates and 1 OR gate.

 

C2 = C0P0P1 + G0P1 + G1

 

Implementation Of C3 & C4–

 

Similarly, we implement C3 and C4.

  • Implementation of C3 uses 3 AND gates and 1 OR gate.
  • Implementation of C4 uses 4 AND gates and 1 OR gate.

 

Total number of gates required to implement carry generators (provided carry propagators Pi and carry generators Gi) are-

  • Total number of AND gates required for addition of 4-bit numbers = 1 + 2 + 3 + 4 = 10.
  • Total number of OR gates required for addition of 4-bit numbers = 1 + 1 + 1 + 1 = 4.

 

General Formula-

 

The following formula is used to calculate number of gates required for evaluating all carry bits-

 

For a n-bit carry look ahead adder to evaluate all the carry bits, it requires-

  • Number of AND gates = n(n+1) / 2
  • Number of OR gates = n

 

Advantages of Carry Look Ahead Adder-

 

The advantages of carry look ahead adder are-

  • It generates the carry-in for each full adder simultaneously.
  • It reduces the propagation delay.

 

Disadvantages of Carry Look Ahead Adder-

 

The disadvantages of carry look ahead adder are-

  • It involves complex hardware.
  • It is costlier since it involves complex hardware.
  • It gets more complicated as the number of bits increases.

 

To gain better understanding about Carry Look Ahead Adder,

Watch this Video Lecture

 

Next Article- K Maps | Karnaugh Maps

 

Get more notes and other study material of Digital Design.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Alternative Logic Gates | Bubbled Gates | Logic Gates

Digital Design

Logic Gates-

 

Before you go through this article, make sure that you have gone through the previous article on Logic Gates.

 

We have discussed-

  • Logic gates are the basic building blocks of any digital circuit.
  • Logic gates are classified as-

 

 

In this article, we will discuss about Alternative Logic Gates.

 

Alternative Logic Gates-

 

Alternative logic gate is an alternate logic gate that produces the same output as the original logic gate

and can be used during the unavailability of the original logic gate to serve the same purpose.

 

Alternative logic gates are also called as Alternate Gates.

Alternative logic gates are also called as Bubbled Gates since they contain bubbles in them.

 

The following table shows the original logic gate and its corresponding alternate gate-

 

 

Also Read- Universal Logic Gates

 

Rules To Memorize Alternative Logic Gates-

 

The following rules are helpful in drawing an alternate logic gate for a given logic gate-

 

For AND, NAND, OR & NOR Gates-

 

  • Both the inputs of alternative gate will have bubbles (which represents NOT gate).
  • For AND structured original gate, alternative gate will be OR structured.
  • For OR structured original gate, alternative gate will be AND structured.
  • If bubble is present at the output of original gate, then no bubble will be present at the output of alternative gate.
  • If bubble is not present at the output of original gate, then a bubble will be present at the output of alternative gate.

 

For EX-OR & EX-NOR Gates-

 

  • One of the inputs of alternative gate will have a bubble (which represents NOT gate).
  • For EX-OR structured original gate, alternative gate will be EX-NOR structured.
  • For EX-NOR structured original gate, alternative gate will be EX-OR structured.
  • If bubble is present at the output of original gate, then no bubble will be present at the output of alternative gate.
  • If bubble is not present at the output of original gate, then a bubble will be present at the output of alternative gate.

 

To gain better understanding about Alternative Logic Gates,

Watch this Video Lecture

 

Next Article- Latches & Flip-Flops

 

Get more notes and other study material of Digital Design.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Self-Dual Functions | Dual Of Boolean Expression

Digital Design

Dual Of Boolean Expression-

 

To get a dual of any Boolean Expression, replace-

  • OR with AND i.e. + with .
  • AND with OR i.e. . with +
  • 1 with 0
  • 0 with 1

 

Dual of Boolean Expression Examples-

 

Following are examples of dual of Boolean Expressions-

 

Example-01:

 

  • Consensus  theorem is xy + x’z + yz = xy + x’z
  • Dual of Consensus theorem is (x + y)(x’ + z)(y + z) = (x + y)(x’ + z)

 

Example-02:

 

  • Boolean expression is xyz + x’yz’ + y’z = 1
  • Dual of the above Boolean expression is (x + y + z)(x’ + y + z’)(y’ + z) = 0

 

Self-Dual Functions-

 

When a function is equal to its dual, it is called as a Self dual function.

 

Example-

 

Consider the function : F (A , B , C) = AB + BC + CA

 

The dual of this function is-

Fd (A , B , C)

= (A + B)(B + C)(C + A)

= AB + BC + CA

 

Clearly, F (A , B , C) = Fd (A , B , C)

∴ F (A , B , C) is a self-dual function.

 

Conditions For Self-Dual Function-

 

The necessary and sufficient conditions for any function to be a self-dual function are-

  • The function must be a Neutral Function.
  • The function must not contain any mutually exclusive terms.

 

Mutually Exclusive Terms

 

Consider we have any term X consisting of some variables.

Then, a term obtained by complementing each variable of term X is called as its mutually exclusive term.

 

Examples-

 

  • (ABC , A’B’C’) are mutually exclusive terms.
  • (AB’C , A’BC’) are mutually exclusive terms.

 

Number of Self-Dual Functions-

 

 

Here n = number of Boolean variables in the function.

 

Explanation-

 

  • For a function to be a self-dual function, the function must be a neutral function.
  • For a function to be a neutral function, number of minterms must be equal to number of maxterms.
  • So, we choose half of the terms i.e. 2n / 2 = 2n-1 terms.
  • Now, for each of these terms, we have two choices whether to include it or not in the self-dual function.

 

So, possible number of self-dual functions

= 2 x 2 x 2 x ……. x 2n-1

= 22^(n-1)

 

Relationship Between Neutral Functions & Self-dual Functions-

 

  • Every self-dual function is surely a neutral function.
  • But every neutral function need not be a self-dual function.

 

 

Important Property of Self-Dual Functions-

 

Self-duality is closed under complementation.

 

Example-

 

  • If the function F (A , B , C) = ∑ (0 , 1 , 2 , 4) is a self-dual function.
  • Then, its complement function F’ (A , B , C) = ∑ (3 , 5 , 6 , 7) will also be a self-dual function.

 

PRACTICE PROBLEM BASED ON SELF-DUAL FUNCTIONS-

 

Problem-

 

Consider the following functions-

  1. F (A , B , C) = ∑ (0 , 2 , 3)
  2. F (A , B , C) = ∑ (0 , 1 , 6 , 7)
  3. F (A , B , C) = ∑ (0 , 1 , 2 , 4)
  4. F (A , B , C) = ∑ (3 , 5 , 6 , 7)

 

Which of the above functions are self-dual functions?

  1. Only (iii)
  2. Only (ii)
  3. Only (iii) and (iv)
  4. All are self-dual functions

 

Solution-

 

Condition-01:

 

According to condition-01, for a function to be a self-dual function, the function must be a neutral function.

 

  • In all the given options, we have functions of 3 variables- A, B and C.
  • So, Neutral function must contain exactly 2n-1 = 23-1 = 4 minterms and 4 maxterms.
  • But Function-(i) contains only 3 minterms. So, it is not a neutral function.
  • Therefore, it can’t be a self-dual function and it gets eliminated.
  • We are now left with three other functions which satisfies condition-01 and are all neutral functions.
  • We will now use 2nd condition to eliminate the incorrect option(s).

 

Condition-02:

 

According to condition-02, a self-dual function must not contain mutually exclusive terms.

First, let us find which terms are mutually exclusive-

 

A B C Minterms
0 0 0 0 A’B’C’
1 0 0 1 A’B’C
2 0 1 0 A’BC’
3 0 1 1 A’BC
4 1 0 0 AB’C’
5 1 0 1 AB’C
6 1 1 0 ABC’
7 1 1 1 ABC

 

  • From here, pairs of mutually exclusive terms are (0,7) , (1,6) , (2,5) , (3,4).
  • Mutually exclusive terms are not allowed in self-dual functions.
  • Therefore, terms inside the pairs can not appear together.
  • But terms 0 and 7 appear together in the function-(ii).
  • So, it can not be a self-dual function.
  • But functions (iii) and (iv) do not contain any mutually exclusive terms.
  • Therefore, functions (iii) and (iv) are self-dual functions.

 

Thus, Option (C) is correct.

 

NOTE-

 

  • Functions (iii) and (iv) are complementary functions.
  • So, if one function is a self-dual function, the other function will also be a self-dual function.
  • This is because self-dual functions are closed under complementation.

 

To gain better understanding about Self-Dual Functions,

Watch this Video Lecture

 

Get more notes and other study material of Digital Design.

Watch video lectures by visiting our YouTube channel LearnVidFun.