Full Adder | Definition | Circuit Diagram | Truth Table

Half Adder-

 

Before you go through this article, make sure that you have gone through the previous article on Half Adder.

 

We have discussed-

• Half Adder is used for the purpose of adding two single bit numbers.
• Half adders have no scope of adding the carry bit resulting from the addition of previous bits.
• To overcome this drawback, full adder comes into play.

 

 

In this article, we will discuss about Full Adder.

 

Full Adder-

 

• Full Adder is a combinational logic circuit.
• It is used for the purpose of adding two single bit numbers with a carry.
• Thus, full adder has the ability to perform the addition of three bits.
• Full adder contains 3 inputs and 2 outputs (sum and carry) as shown-

 

 

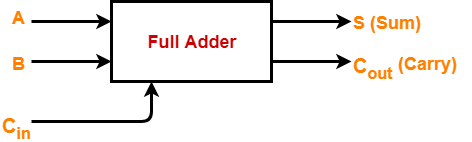
Full Adder Designing-

 

Full adder is designed in the following steps-

 

Step-01:

 

Identify the input and output variables-

• Input variables = A, B, C_in (either 0 or 1)
• Output variables = S, C_out where S = Sum and C_out = Carry

 

Step-02:

 

Draw the truth table-

 

Inputs			Outputs
A	B	Cin	Cout (Carry)	S (Sum)
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

Truth Table

 

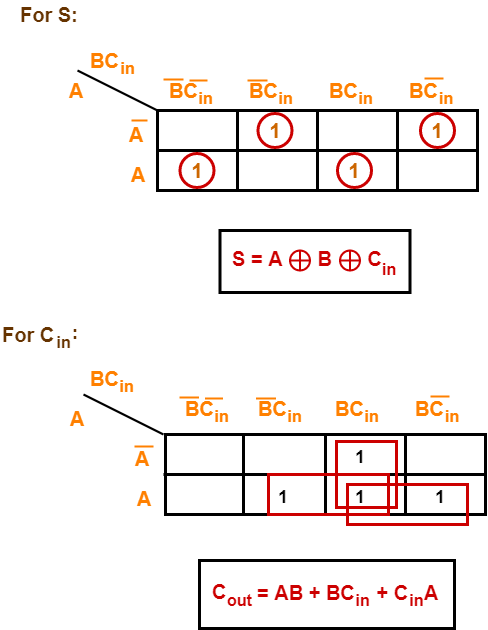
Step-03:

 

Draw K-maps using the above truth table and determine the simplified Boolean expressions-

 

 

Also Read- Full Subtractor

 

Step-04:

 

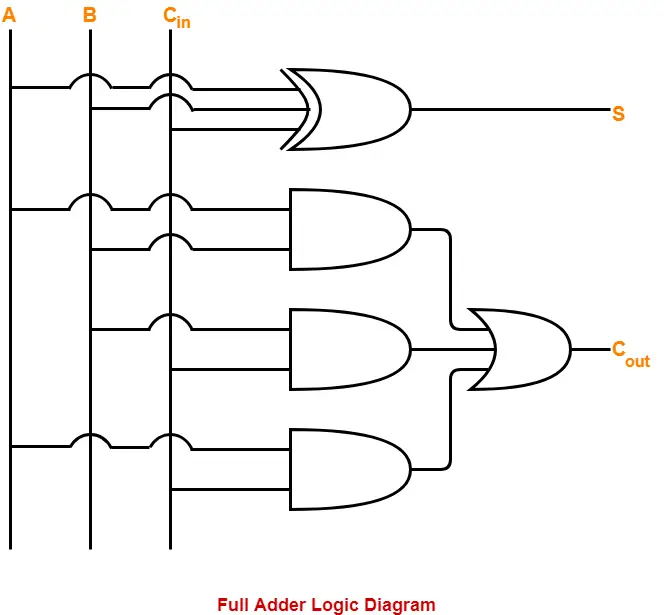
Draw the logic diagram.

The implementation of full adder using 1 XOR gate, 3 AND gates and 1 OR gate is as shown below-

 

 

To gain better understanding about Full Adder,

Watch this Video Lecture

 

Next Article- Half Subtractor

 

Get more notes and other study material of Digital Design.

Watch video lectures by visiting our YouTube channel LearnVidFun.