Ripple Carry Adder | 4 bit Ripple Carry Adder

Ripple Carry Adder-

 

• Ripple Carry Adder is a combinational logic circuit.
• It is used for the purpose of adding two n-bit binary numbers.
• It requires n full adders in its circuit for adding two n-bit binary numbers.
• It is also known as n-bit parallel adder.

 

4-bit Ripple Carry Adder-

 

4-bit ripple carry adder is used for the purpose of adding two 4-bit binary numbers.

 

In Mathematics, any two 4-bit binary numbers A₃A₂A₁A₀ and B₃B₂B₁B₀ are added as shown below-

 

 

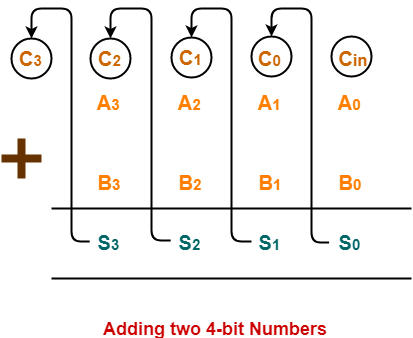
Using ripple carry adder, this addition is carried out as shown by the following logic diagram-

 

 

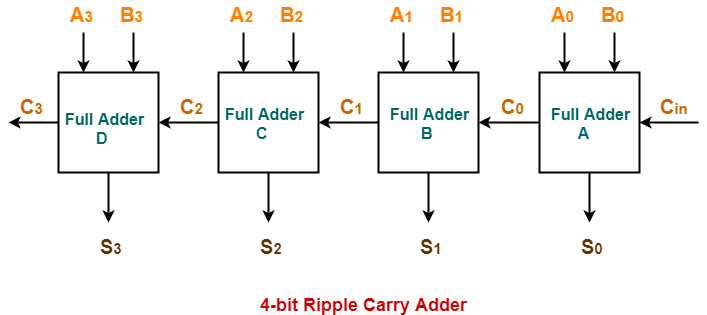
As shown-

• Ripple Carry Adder works in different stages.
• Each full adder takes the carry-in as input and produces carry-out and sum bit as output.
• The carry-out produced by a full adder serves as carry-in for its adjacent most significant full adder.
• When carry-in becomes available to the full adder, it activates the full adder.
• After full adder becomes activated, it comes into operation.

 

Also Read- Full Adder Working

 

Working Of 4-bit Ripple Carry Adder-

 

Let-

• The two 4-bit numbers are 0101 (A₃A₂A₁A₀) and 1010 (B₃B₂B₁B₀).
• These numbers are to be added using a 4-bit ripple carry adder.

 

4-bit Ripple Carry Adder carries out the addition as explained in the following stages-

 

Stage-01:

 

• When C_in is fed as input to the full Adder A, it activates the full adder A.
• Then at full adder A, A₀ = 1, B₀ = 0, C_in = 0.

 

Full adder A computes the sum bit and carry bit as-

 

Calculation of S₀–

 

S₀ = A₀ ⊕  B₀ ⊕ C_in

S₀ = 1 ⊕ 0 ⊕ 0

S₀ = 1

 

Calculation of C₀–

 

C₀ = A₀B₀ ⊕  B₀C_in ⊕ C_inA₀

C₀ = 1.0 ⊕ 0.0 ⊕ 0.1

C₀ = 0 ⊕ 0 ⊕ 0

C₀ = 0

 

Stage-02:

 

• When C₀ is fed as input to the full adder B, it activates the full adder B.
• Then at full adder B, A₁ = 0, B₁ = 1, C₀ = 0.

 

Full adder B computes the sum bit and carry bit as-

 

Calculation of S₁–

 

S₁ = A₁ ⊕  B₁ ⊕ C₀

S₁ = 0 ⊕ 1 ⊕ 0

S₁ = 1

 

Calculation of C₁–

 

C₁ = A₁B₁ ⊕  B₁C₀ ⊕ C₀A₁

C₁ = 0.1 ⊕ 1.0 ⊕ 0.0

C₁ = 0 ⊕ 0 ⊕ 0

C₁ = 0

 

Stage-03:

 

• When C₁ is fed as input to the full adder C, it activates the full adder C.
• Then at full adder C, A₂ = 1, B₂ = 0, C₁ = 0.

 

Full adder C computes the sum bit and carry bit as-

 

Calculation of S₂–

 

S₂ = A₂ ⊕  B₂ ⊕ C₁

S₂ = 1 ⊕ 0 ⊕ 0

S₂ = 1

 

Calculation of C₂–

 

C₂ = A₂B₂ ⊕  B₂C₁ ⊕ C₁A₂

C₂ = 1.0 ⊕ 0.0 ⊕ 0.1

C₂ = 0 ⊕ 0 ⊕ 0

C₂ = 0

 

Stage-04:

 

• When C₂ is fed as input to the full adder D, it activates the full adder D.
• Then at full adder D, A₃ = 0, B₃ = 1, C₂ = 0.

 

Full adder D computes the sum bit and carry bit as-

 

Calculation of S₃–

 

S₃ = A₃ ⊕  B₃ ⊕ C₂

S₃ = 0 ⊕ 1 ⊕ 0

S₃ = 1

 

Calculation of C₃–

 

C₃ = A₃B₃ ⊕  B₃C₂ ⊕ C₂A₃

C₃ = 0.1 ⊕ 1.0 ⊕ 0.0

C₃ = 0 ⊕ 0 ⊕ 0

C₃ = 0

 

Thus finally,

• Output Sum = S₃S₂S₁S₀ = 1111
• Output Carry = C₃ = 0

 

Why Ripple Carry Adder is Called So?   In Ripple Carry Adder, The carry out produced by each full adder serves as carry-in for its adjacent most significant full adder. Each carry bit ripples or waves into the next stage. That’s why, it is called as “Ripple Carry Adder”.

 

Disadvantages of Ripple Carry Adder-

 

• Ripple Carry Adder does not allow to use all the full adders simultaneously.
• Each full adder has to necessarily wait until the carry bit becomes available from its adjacent full adder.
• This increases the propagation time.
• Due to this reason, ripple carry adder becomes extremely slow.
• This is considered to be the biggest disadvantage of using ripple carry adder.

 

To overcome this disadvantage, Carry Look Ahead Adder comes into play.

 

To gain better understanding about Ripple Carry Adder,

Watch this Video Lecture

 

Next Article- Delay in Ripple Carry Adder

 

Get more notes and other study material of Digital Design.

Watch video lectures by visiting our YouTube channel LearnVidFun.