Types of Graphs-
Before you go through this article, make sure that you have gone through the previous article on various Types of Graphs in Graph Theory.
We have discussed-
- A graph is a collection of vertices connected to each other through a set of edges.
- The study of graphs is known as Graph Theory.

In this article, we will discuss about Bipartite Graphs.
Bipartite Graph-
A bipartite graph is a special kind of graph with the following properties-
- It consists of two sets of vertices X and Y.
- The vertices of set X join only with the vertices of set Y.
- The vertices within the same set do not join.
Bipartite Graph Example-
The following graph is an example of a bipartite graph-
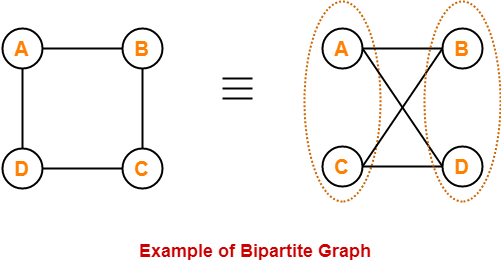
Here,
- The vertices of the graph can be decomposed into two sets.
- The two sets are X = {A, C} and Y = {B, D}.
- The vertices of set X join only with the vertices of set Y and vice-versa.
- The vertices within the same set do not join.
- Therefore, it is a bipartite graph.
Also Read- Planar Graph
Complete Bipartite Graph-
A complete bipartite graph may be defined as follows-
| A bipartite graph where every vertex of set X is joined to every vertex of set Y
is called as complete bipartite graph. OR Complete bipartite graph is a bipartite graph which is complete. OR Complete bipartite graph is a graph which is bipartite as well as complete. |
Complete Bipartite Graph Example-
The following graph is an example of a complete bipartite graph-
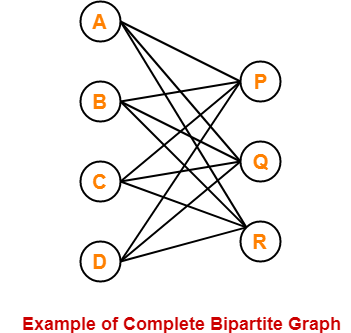
Here,
- This graph is a bipartite graph as well as a complete graph.
- Therefore, it is a complete bipartite graph.
- This graph is called as K4,3.
Bipartite Graph Chromatic Number-
To properly color any bipartite graph,
- Minimum 2 colors are required.
- This ensures that the end vertices of every edge are colored with different colors.
- Thus, bipartite graphs are 2-colorable.
NoteIf graph is bipartite with no edges, then it is 1-colorable. |
Example-
The chromatic number of the following bipartite graph is 2-
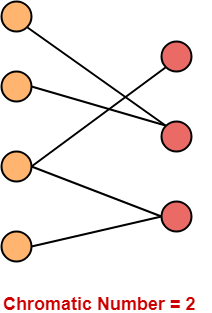
Bipartite Graph Properties-
Few important properties of bipartite graph are-
- Bipartite graphs are 2-colorable.
- Bipartite graphs contain no odd cycles.
- Every sub graph of a bipartite graph is itself bipartite.
- There does not exist a perfect matching for a bipartite graph with bipartition X and Y if |X| ≠ |Y|.
- In any bipartite graph with bipartition X and Y,
Sum of degree of vertices of set X = Sum of degree of vertices of set Y
Bipartite Graph Perfect Matching-
| Number of complete matchings for Kn,n = n! |
Given a bipartite graph G with bipartition X and Y,
- There does not exist a perfect matching for G if |X| ≠ |Y|.
- A perfect matching exists on a bipartite graph G with bipartition X and Y if and only if for all the subsets of X, the number of elements in the subset is less than or equal to the number of elements in the neighborhood of the subset.
Maximum Number Of Edges-
- Any bipartite graph consisting of ‘n’ vertices can have at most (1/4) x n2 edges.
- Maximum possible number of edges in a bipartite graph on ‘n’ vertices = (1/4) x n2.
Explanation
|
Also Read- Euler Graph & Hamiltonian Graph
PRACTICE PROBLEMS BASED ON BIPARTITE GRAPH IN GRAPH THEORY-
Problem-01:
Is the following graph a bipartite graph?
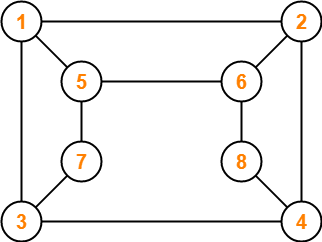
Solution-
The given graph may be redrawn as-
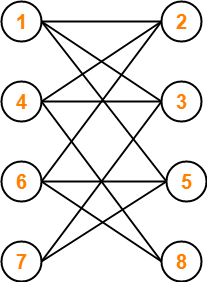
Here,
- This graph consists of two sets of vertices.
- The two sets are X = {1, 4, 6, 7} and Y = {2, 3, 5, 8}.
- The vertices of set X are joined only with the vertices of set Y and vice-versa.
- Also, any two vertices within the same set are not joined.
- This satisfies the definition of a bipartite graph.
Therefore, Given graph is a bipartite graph.
Problem-02:
The maximum number of edges in a bipartite graph on 12 vertices is _________?
Solution-
We know, Maximum possible number of edges in a bipartite graph on ‘n’ vertices = (1/4) x n2.
Substituting n = 12, we get-
Maximum number of edges in a bipartite graph on 12 vertices
= (1/4) x (12)2
= (1/4) x 12 x 12
= 36
Therefore, Maximum number of edges in a bipartite graph on 12 vertices = 36.
To gain better understanding about Bipartite Graphs in Graph Theory,
Next Article- Konigsberg Bridge Problem
Get more notes and other study material of Graph Theory.
Watch video lectures by visiting our YouTube channel LearnVidFun.