Three Address Code | DAGs | Basic Blocks & Flow Graphs-
Before you go through this article, make sure that you have gone through the previous articles on-
In this article, we will solve Miscellaneous Problems based on these Concepts.
PRACTICE PROBLEMS BASED ON ABOVE CONCEPTS-
Problem-01:
Generate three address code for the following code-
c = 0
do
{
if (a < b) then
x++;
else
x–;
c++;
} while (c < 5)
Solution-
Three address code for the given code is-
- c = 0
- if (a < b) goto (4)
- goto (7)
- T1 = x + 1
- x = T1
- goto (9)
- T2 = x – 1
- x = T2
- T3 = c + 1
- c = T3
- if (c < 5) goto (2)
Problem-02:
Generate three address code for the following code-
while (A < C and B > D) do
if A = 1 then C = C + 1
else
while A <= D
do A = A + B
Solution-
Three address code for the given code is-
- if (A < C) goto (3)
- goto (15)
- if (B > D) goto (5)
- goto (15)
- if (A = 1) goto (7)
- goto (10)
- T1 = c + 1
- c = T1
- goto (1)
- if (A <= D) goto (12)
- goto (1)
- T2 = A + B
- A = T2
- goto (10)
Problem-03:
Generate three address code for the following code-
switch (ch)
{
case 1 : c = a + b;
break;
case 2 : c = a – b;
break;
}
Solution-
Three address code for the given code is-
if ch = 1 goto L1
if ch = 2 goto L2
L1:
T1 = a + b
c = T1
goto Last
L2:
T1 = a – b
c = T2
goto Last
Last:
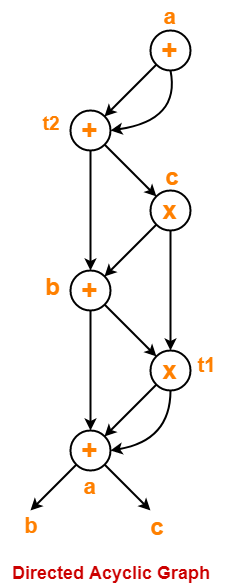
Problem-04:
Construct a DAG for the following three address code-
- a = b + c
- t1 = a x a
- b = t1 + a
- c = t1 x b
- t2 = c + b
- a = t2 + t2
Solution-
Directed acyclic graph for the given three address code is-
Problem-05:
Consider the following code-
prod = 0 ;
i = 1 ;
do
{
prod = prod + a[ i ] x b[ i ] ;
i = i + 1 ;
} while (i <= 10) ;
- Compute the three address code.
- Compute the basic blocks and draw the flow graph.
Solution-
Part-01:
Three address code for the given code is-
prod = 0
i = 1
T1 = 4 x i
T2 = a[T1]
T3 = 4 x i
T4 = b[T3]
T5 = T2 x T4
T6 = T5 + prod
prod = T6
T7 = i + 1
i = T7
if (i <= 10) goto (3)
Part-02:
Step-01:
We identify the leader statements as-
- prod = 0 is a leader because first statement is a leader.
- T1 = 4 x i is a leader because target of conditional or unconditional goto is a leader.
Step-02:
The above generated three address code can be partitioned into 2 basic blocks as-

Step-03:
The flow graph is-

To gain better understanding about these Miscellaneous Problems,
Download Handwritten Notes Here-
Next Article- Code Optimization
Get more notes and other study material of Compiler Design.
Watch video lectures by visiting our YouTube channel LearnVidFun.