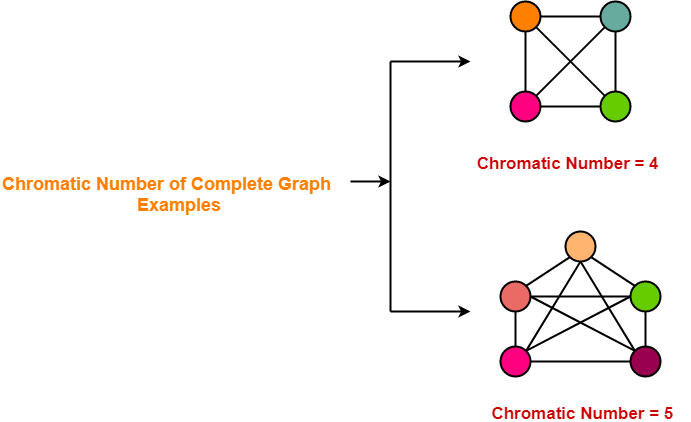
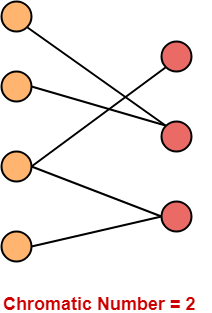
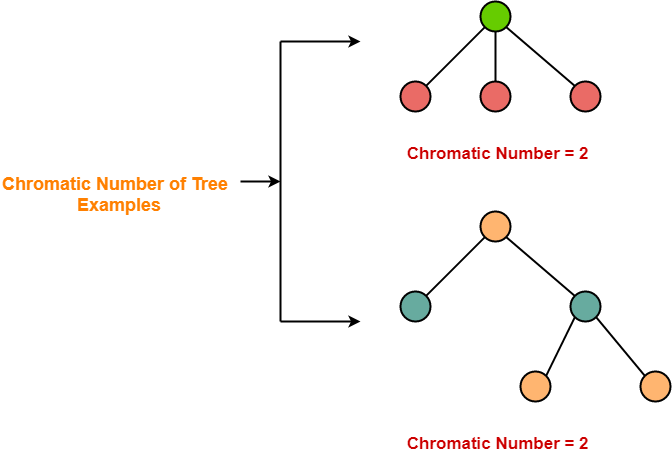
Chromatic Number-
Before you go through this article, make sure that you have gone through the previous article on Chromatic Number.
We gave discussed-
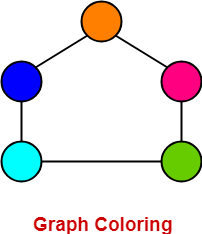
- Graph Coloring is a process of assigning colors to the vertices of a graph.
- It ensures that no two adjacent vertices of the graph are colored with the same color.
- Chromatic Number is the minimum number of colors required to properly color any graph.
In this article, we will discuss how to find Chromatic Number of any graph.
Graph Coloring Algorithm-
- There exists no efficient algorithm for coloring a graph with minimum number of colors.
- Graph Coloring is a NP complete problem.
However, a following greedy algorithm is known for finding the chromatic number of any given graph.
Greedy Algorithm-
Step-01:
Color first vertex with the first color.
Step-02:
Now, consider the remaining (V-1) vertices one by one and do the following-
- Color the currently picked vertex with the lowest numbered color if it has not been used to color any of its adjacent vertices.
- If it has been used, then choose the next least numbered color.
- If all the previously used colors have been used, then assign a new color to the currently picked vertex.
Drawbacks of Greedy Algorithm-
There are following drawbacks of the above Greedy Algorithm-
- The above algorithm does not always use minimum number of colors.
- The number of colors used sometimes depend on the order in which the vertices are processed.
Also Read- Types of Graphs in Graph Theory
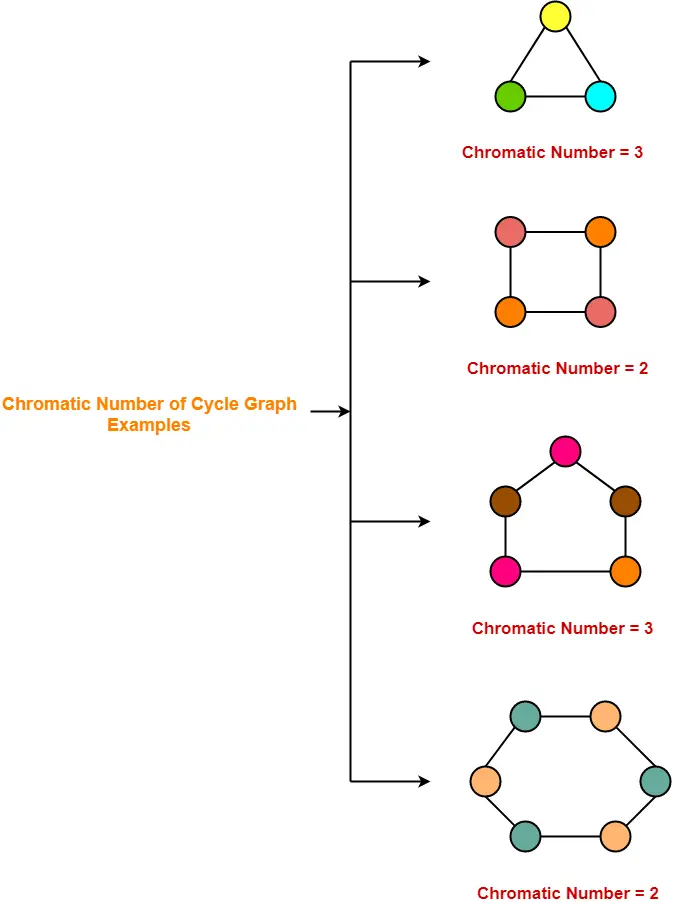
PRACTICE PROBLEMS BASED ON FINDING CHROMATIC NUMBER OF A GRAPH-
Problem-01:
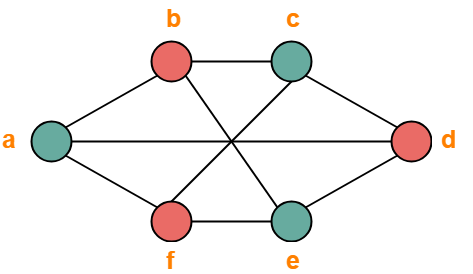
Find chromatic number of the following graph-
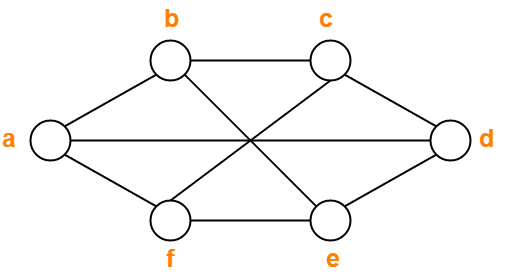
Solution-
Applying Greedy Algorithm, we have-
| Vertex | a | b | c | d | e | f |
| Color | C1 | C2 | C1 | C2 | C1 | C2 |
From here,
- Minimum number of colors used to color the given graph are 2.
- Therefore, Chromatic Number of the given graph = 2.
The given graph may be properly colored using 2 colors as shown below-
Problem-02:
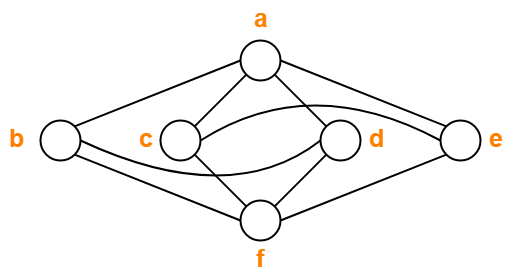
Find chromatic number of the following graph-
Solution-
Applying Greedy Algorithm, we have-
| Vertex | a | b | c | d | e | f |
| Color | C1 | C2 | C2 | C3 | C3 | C1 |
From here,
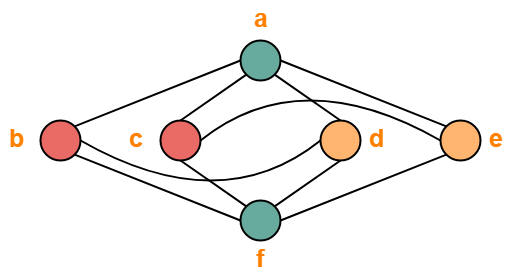
- Minimum number of colors used to color the given graph are 3.
- Therefore, Chromatic Number of the given graph = 3.
The given graph may be properly colored using 3 colors as shown below-
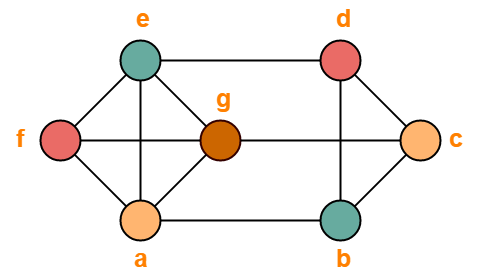
Problem-03:
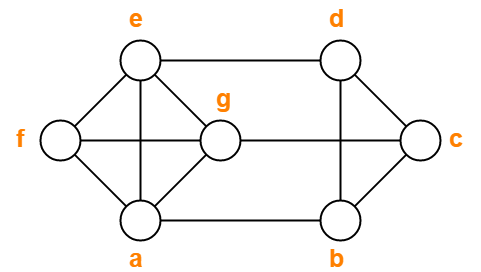
Find chromatic number of the following graph-
Solution-
Applying Greedy Algorithm, we have-
| Vertex | a | b | c | d | e | f | g |
| Color | C1 | C2 | C1 | C3 | C2 | C3 | C4 |
From here,
- Minimum number of colors used to color the given graph are 4.
- Therefore, Chromatic Number of the given graph = 4.
The given graph may be properly colored using 4 colors as shown below-
Problem-04:
Find chromatic number of the following graph-
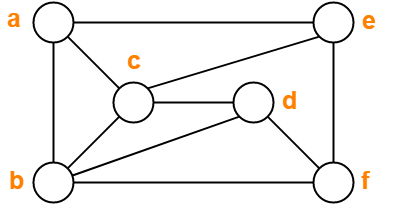
Solution-
Applying Greedy Algorithm, we have-
| Vertex | a | b | c | d | e | f |
| Color | C1 | C2 | C3 | C1 | C2 | C3 |
From here,
- Minimum number of colors used to color the given graph are 3.
- Therefore, Chromatic Number of the given graph = 3.
The given graph may be properly colored using 3 colors as shown below-
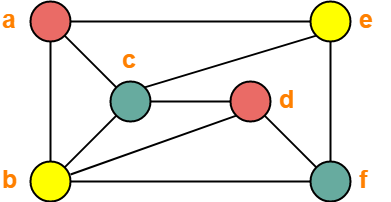
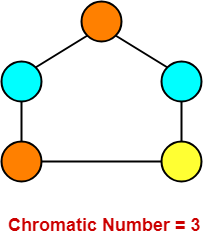
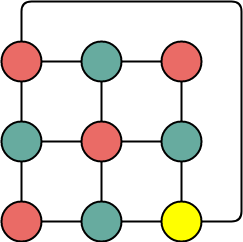
Problem-05:
Find chromatic number of the following graph-
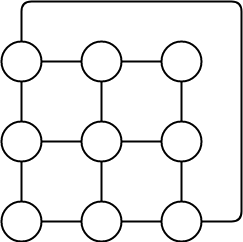
Solution-
Applying Greedy Algorithm,
- Minimum number of colors required to color the given graph are 3.
- Therefore, Chromatic Number of the given graph = 3.
The given graph may be properly colored using 3 colors as shown below-
To gain better understanding about How to Find Chromatic Number,
Get more notes and other study material of Graph Theory.
Watch video lectures by visiting our YouTube channel LearnVidFun.