Graph Coloring in Graph Theory | Chromatic Number of Graphs

Graph Coloring-

 

Graph Coloring is a process of assigning colors to the vertices of a graph such that no two adjacent vertices of it are assigned the same color.

 

• Graph Coloring is also called as Vertex Coloring.
• It ensures that there exists no edge in the graph whose end vertices are colored with the same color.
• Such a graph is called as a Properly colored graph.

 

Graph Coloring Example-

 

The following graph is an example of a properly colored graph-

 

 

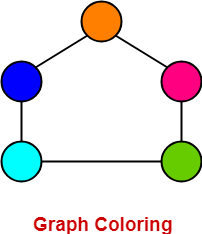
In this graph,

• No two adjacent vertices are colored with the same color.
• Therefore, it is a properly colored graph.

 

Graph Coloring Applications-

 

Some important applications of graph coloring are as follows-

• Map Coloring
• Scheduling the tasks
• Preparing Time Table
• Assignment
• Conflict Resolution
• Sudoku

 

Chromatic Number-

 

Chromatic Number is the minimum number of colors required to properly color any graph. OR Chromatic Number is the minimum number of colors required to color any graph such that no two adjacent vertices of it are assigned the same color.

 

Chromatic Number Example-

 

Consider the following graph-

 

 

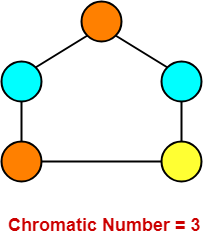
In this graph,

• No two adjacent vertices are colored with the same color.
• Minimum number of colors required to properly color the vertices = 3.
• Therefore, Chromatic number of this graph = 3.
• We can not properly color this graph with less than 3 colors.

 

Also Read- Types of Graphs in Graph Theory

 

Chromatic Number Of Graphs-

 

Chromatic Number of some common types of graphs are as follows-

 

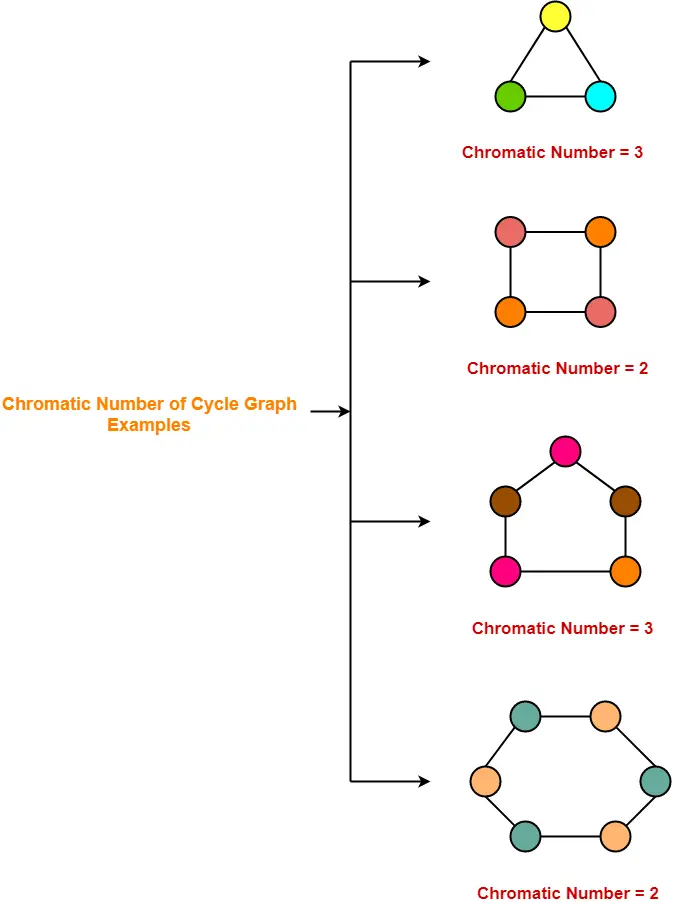
1. Cycle Graph-

 

• A simple graph of ‘n’ vertices (n>=3) and ‘n’ edges forming a cycle of length ‘n’ is called as a cycle graph.
• In a cycle graph, all the vertices are of degree 2.

 

Chromatic Number If number of vertices in cycle graph is even, then its chromatic number = 2. If number of vertices in cycle graph is odd, then its chromatic number = 3.

 

Examples-

 

 

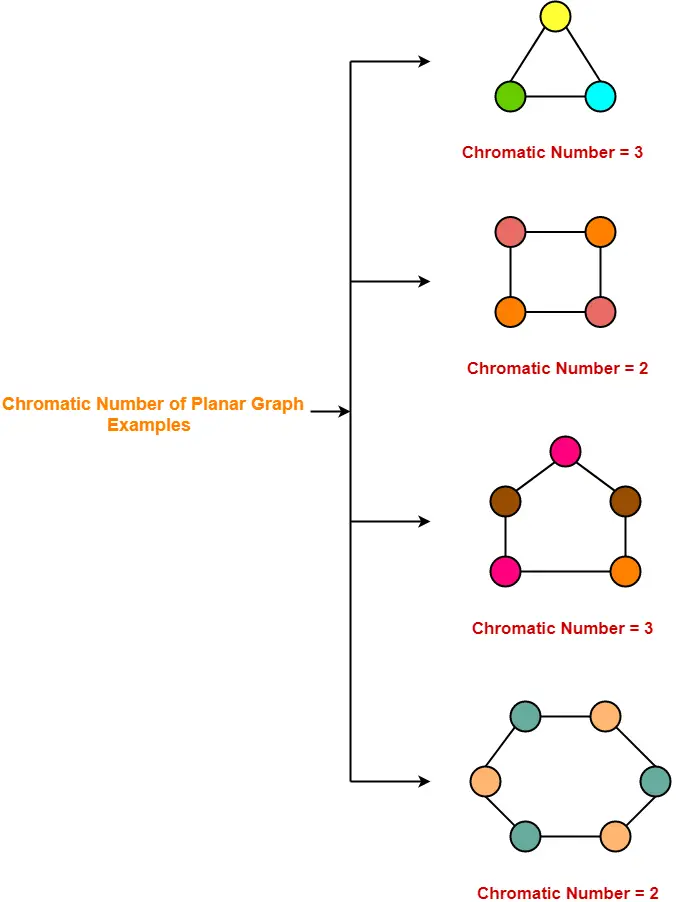
2. Planar Graphs-

 

A Planar Graph is a graph that can be drawn in a plane such that none of its edges cross each other.

 

Chromatic Number Chromatic Number of any Planar Graph = Less than or equal to 4

 

Examples-

 

• All the above cycle graphs are also planar graphs.
• Chromatic number of each graph is less than or equal to 4.

 

 

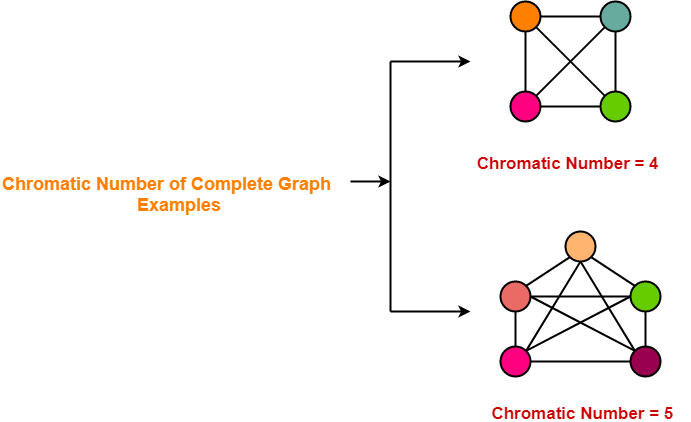
3. Complete Graphs-

 

• A complete graph is a graph in which every two distinct vertices are joined by exactly one edge.
• In a complete graph, each vertex is connected with every other vertex.
• So to properly it, as many different colors are needed as there are number of vertices in the given graph.

 

Chromatic Number Chromatic Number of any Complete Graph = Number of vertices in that Complete Graph

 

Examples-

 

 

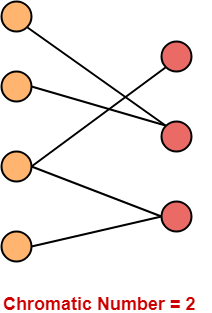
4. Bipartite Graphs-

 

• A Bipartite Graph consists of two sets of vertices X and Y.
• The edges only join vertices in X to vertices in Y, not vertices within a set.

 

Chromatic Number Chromatic Number of any Bipartite Graph = 2

 

Example-

 

 

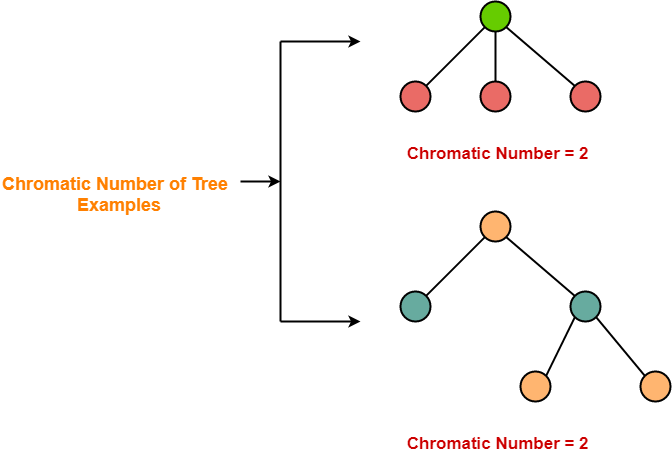
5. Trees-

 

• A Tree is a special type of connected graph in which there are no circuits.
• Every tree is a bipartite graph.
• So, chromatic number of a tree with any number of vertices = 2.

 

Chromatic Number Chromatic Number of any tree = 2

 

Examples-

 

 

To gain better understanding about Graph Coloring & Chromatic Number,

Watch this Video Lecture

 

Next Article- Graph Coloring Algorithm

 

Get more notes and other study material of Graph Theory.

Watch video lectures by visiting our YouTube channel LearnVidFun.