Bubble Sort-
- Bubble sort is the easiest sorting algorithm to implement.
- It is inspired by observing the behavior of air bubbles over foam.
- It is an in-place sorting algorithm.
- It uses no auxiliary data structures (extra space) while sorting.
How Bubble Sort Works?
- Bubble sort uses multiple passes (scans) through an array.
- In each pass, bubble sort compares the adjacent elements of the array.
- It then swaps the two elements if they are in the wrong order.
- In each pass, bubble sort places the next largest element to its proper position.
- In short, it bubbles down the largest element to its correct position.
Bubble Sort Algorithm-
The bubble sort algorithm is given below-
for(int pass=1 ; pass<=n-1 ; ++pass) // Making passes through array
{
for(int i=0 ; i<=n-2 ; ++i)
{
if(A[i] > A[i+1]) // If adjacent elements are in wrong order
swap(i,i+1,A); // Swap them
}
}
//swap function : Exchange elements from array A at position x,y
void swap(int x, int y, int[] A)
{
int temp = A[x];
A[x] = A[y];
A[y] = temp;
return ;
}
// pass : Variable to count the number of passes that are done till now
// n : Size of the array
// i : Variable to traverse the array A
// swap() : Function to swap two numbers from the array
// x,y : Indices of the array that needs to be swapped
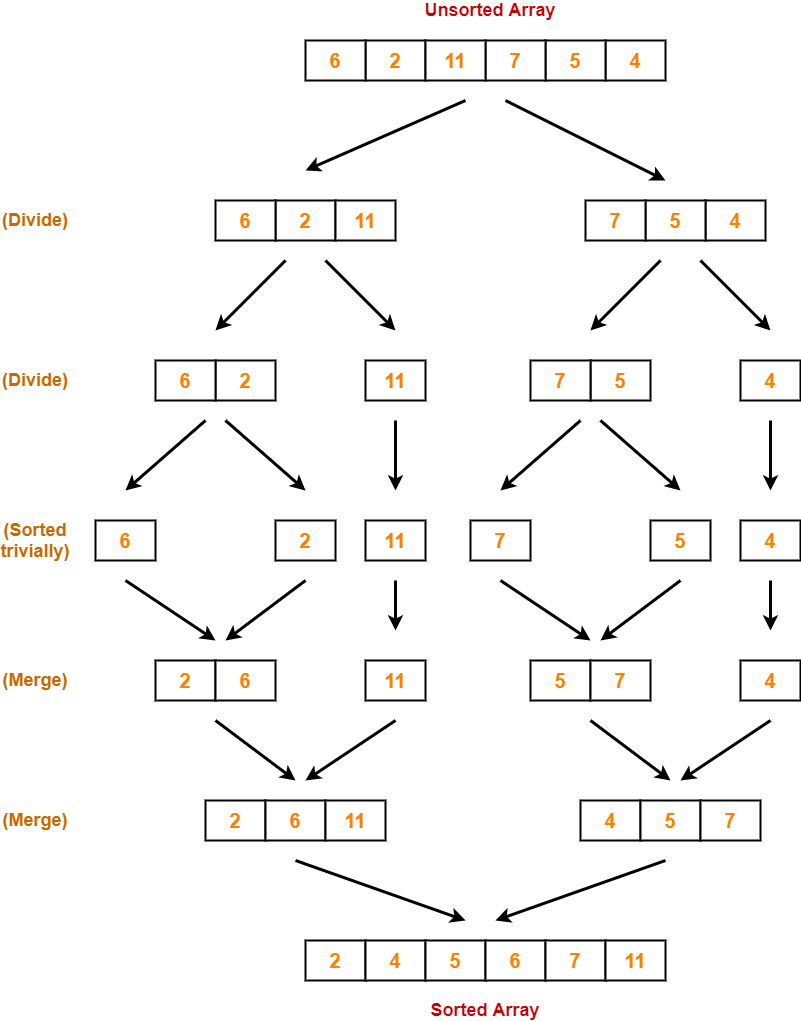
Bubble Sort Example-
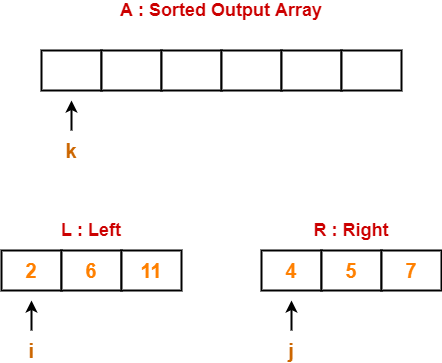
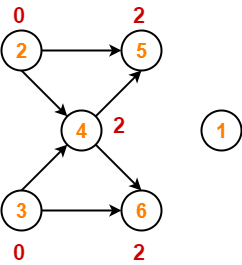
Consider the following array A-

Now, we shall implement the above bubble sort algorithm on this array.
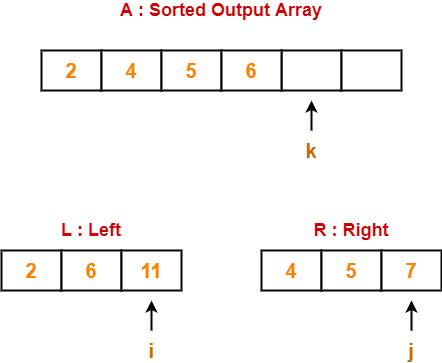
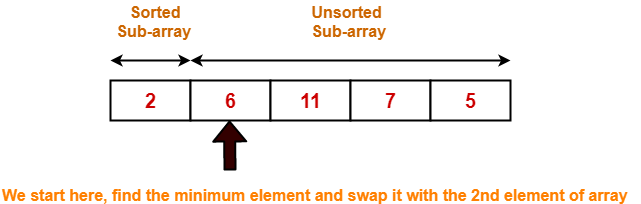
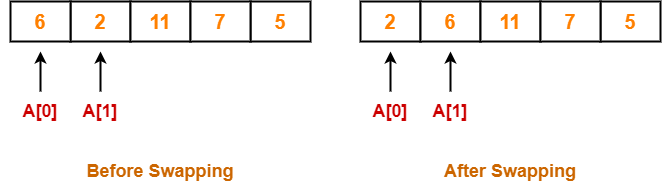
Step-01:
- We have pass=1 and i=0.
- We perform the comparison A[0] > A[1] and swaps if the 0th element is greater than the 1th element.
- Since 6 > 2, so we swap the two elements.
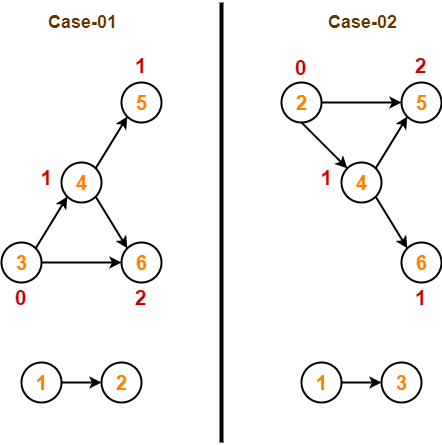
Step-02:
- We have pass=1 and i=1.
- We perform the comparison A[1] > A[2] and swaps if the 1th element is greater than the 2th element.
- Since 6 < 11, so no swapping is required.

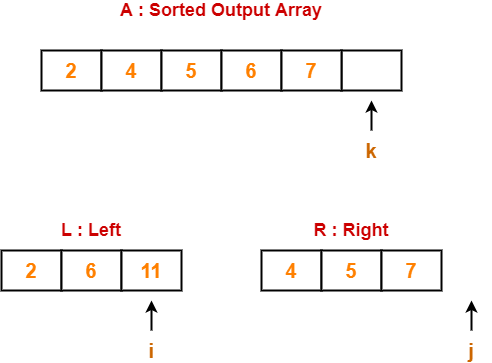
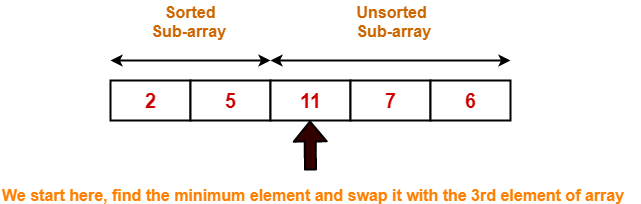
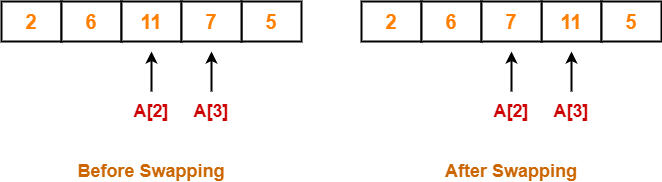
Step-03:
- We have pass=1 and i=2.
- We perform the comparison A[2] > A[3] and swaps if the 2nd element is greater than the 3rd element.
- Since 11 > 7, so we swap the two elements.
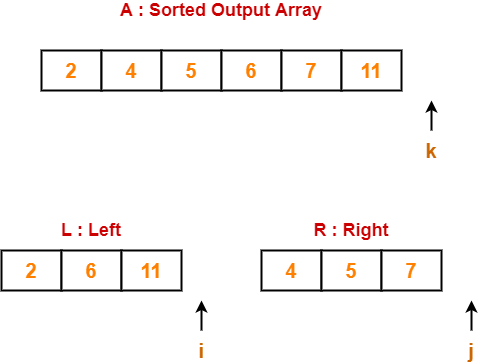
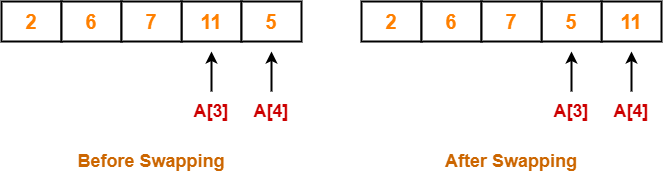
Step-04:
- We have pass=1 and i=3.
- We perform the comparison A[3] > A[4] and swaps if the 3rd element is greater than the 4th element.
- Since 11 > 5, so we swap the two elements.
Finally after the first pass, we see that the largest element 11 reaches its correct position.
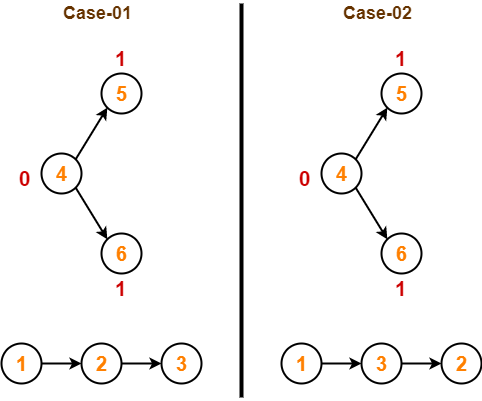
Step-05:
- Similarly after pass=2, element 7 reaches its correct position.
- The modified array after pass=2 is shown below-
![]()
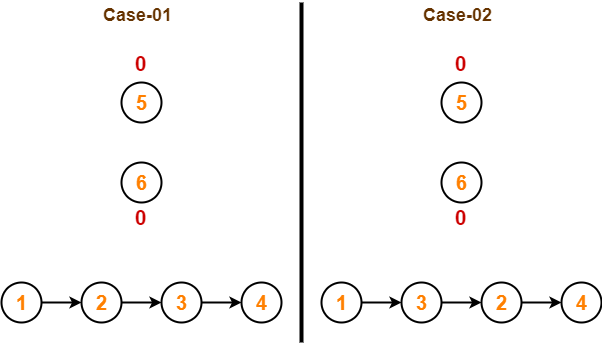
Step-06:
- Similarly after pass=3, element 6 reaches its correct position.
- The modified array after pass=3 is shown below-
![]()
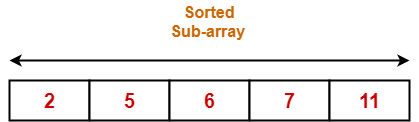
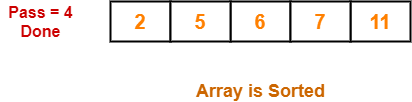
Step-07:
- No further improvement is done in pass=4.
- This is because at this point, elements 2 and 5 are already present at their correct positions.
- The loop terminates after pass=4.
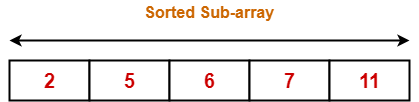
- Finally, the array after pass=4 is shown below-
Optimization Of Bubble Sort Algorithm-
- If the array gets sorted after a few passes like one or two, then ideally the algorithm should terminate.
- But still the above algorithm executes the remaining passes which costs extra comparisons.
Optimized Bubble Sort Algorithm-
The optimized bubble sort algorithm is shown below-
for (int pass=1 ; pass<=n-1 ; ++pass)
{
flag=0 // flag denotes are there any swaps done in pass
for (int i=0 ; i<=n-2 ; ++i)
{
if(A[i] > A[i+1])
{
swap(i,i+1,A);
flag=1 // After swap, set flag to 1
}
}
if(flag == 0) break; // No swaps indicates we can terminate loop
}
void swap(int x, int y, int[] A)
{
int temp = A[x];
A[x] = A[y];
A[y] = temp;
return;
}
Explanation-
- To avoid extra comparisons, we maintain a flag variable.
- The flag variable helps to break the outer loop of passes after obtaining the sorted array.
- The initial value of the flag variable is set to 0.
- The zero value of flag variable denotes that we have not encountered any swaps.
- Once we need to swap adjacent values for correcting their wrong order, the value of flag variable is set to 1.
- If we encounter a pass where flag == 0, then it is safe to break the outer loop and declare the array is sorted.
Time Complexity Analysis-
- Bubble sort uses two loops- inner loop and outer loop.
- The inner loop deterministically performs O(n) comparisons.
Worst Case-
- In worst case, the outer loop runs O(n) times.
- Hence, the worst case time complexity of bubble sort is O(n x n) = O(n2).
Best Case-
- In best case, the array is already sorted but still to check, bubble sort performs O(n) comparisons.
- Hence, the best case time complexity of bubble sort is O(n).
Average Case-
- In average case, bubble sort may require (n/2) passes and O(n) comparisons for each pass.
- Hence, the average case time complexity of bubble sort is O(n/2 x n) = Θ(n2).
The following table summarizes the time complexities of bubble sort in each case-
| Time Complexity | |
| Best Case | O(n) |
| Average Case | Θ(n2) |
| Worst Case | O(n2) |
From here, it is clear that bubble sort is not at all efficient in terms of time complexity of its algorithm.
Space Complexity Analysis-
- Bubble sort uses only a constant amount of extra space for variables like flag, i, n.
- Hence, the space complexity of bubble sort is O(1).
- It is an in-place sorting algorithm i.e. it modifies elements of the original array to sort the given array.
Properties-
Some of the important properties of bubble sort algorithm are-
- Bubble sort is a stable sorting algorithm.
- Bubble sort is an in-place sorting algorithm.
- The worst case time complexity of bubble sort algorithm is O(n2).
- The space complexity of bubble sort algorithm is O(1).
- Number of swaps in bubble sort = Number of inversion pairs present in the given array.
- Bubble sort is beneficial when array elements are less and the array is nearly sorted.
PRACTICE PROBLEMS BASED ON MERGE SORT ALGORITHM-
Problem-01:
The number of swapping needed to sort the numbers 8, 22, 7, 9, 31, 5, 13 in ascending order using bubble sort is- (ISRO CS 2017)
- 11
- 12
- 13
- 10
Solution-
In bubble sort, Number of swaps required = Number of inversion pairs.
Here, there are 10 inversion pairs present which are-
- (8,7)
- (22,7)
- (22,9)
- (8,5)
- (22,5)
- (7,5)
- (9,5)
- (31,5)
- (22,13)
- (31,13)
Thus, Option (D) is correct.
Problem-02:
When will bubble sort take worst-case time complexity?
- The array is sorted in ascending order.
- The array is sorted in descending order.
- Only the first half of the array is sorted.
- Only the second half of the array is sorted.
Solution-
- In bubble sort, Number of swaps required = Number of inversion pairs.
- When an array is sorted in descending order, the number of inversion pairs = n(n-1)/2 which is maximum for any permutation of array.
Thus, Option (B) is correct.
To gain better understanding about Bubble Sort Algorithm,
Next Article- Insertion Sort
Other Popular Sorting Algorithms-
Get more notes and other study material of Design and Analysis of Algorithms.
Watch video lectures by visiting our YouTube channel LearnVidFun.