Selection Sort Algorithm | Example | Time Complexity

Selection Sort-

 

• Selection sort is one of the easiest approaches to sorting.
• It is inspired from the way in which we sort things out in day to day life.
• It is an in-place sorting algorithm because it uses no auxiliary data structures while sorting.

 

How Selection Sort Works?

 

Consider the following elements are to be sorted in ascending order using selection sort-

6, 2, 11, 7, 5

 

Selection sort works as-

• It finds the first smallest element (2).
• It swaps it with the first element of the unordered list.
• It finds the second smallest element (5).
• It swaps it with the second element of the unordered list.
• Similarly, it continues to sort the given elements.

 

As a result, sorted elements in ascending order are-

2, 5, 6, 7, 11

 

Selection Sort Algorithm-

 

Let A be an array with n elements. Then, selection sort algorithm used for sorting is as follows-

 

for (i = 0 ; i < n-1 ; i++)

{

   index = i;

   for(j = i+1 ; j < n ; j++)

   {

      if(A[j] < A[index])

      index = j;

   }

   temp = A[i];

   A[i] = A[index];

   A[index] = temp;

}

 

Here,

• i = variable to traverse the array A
• index = variable to store the index of minimum element
• j = variable to traverse the unsorted sub-array
• temp = temporary variable used for swapping

 

Selection Sort Example-

 

Consider the following elements are to be sorted in ascending order-

6, 2, 11, 7, 5

 

The above selection sort algorithm works as illustrated below-

 

Step-01: For i = 0

 

 

Step-02: For i = 1

 

 

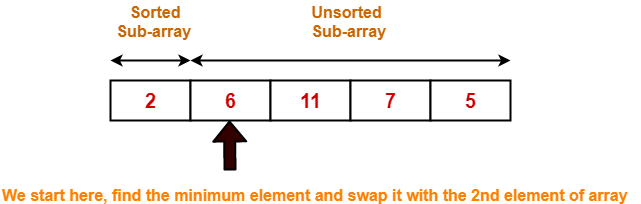
Step-03: For i = 2

 

 

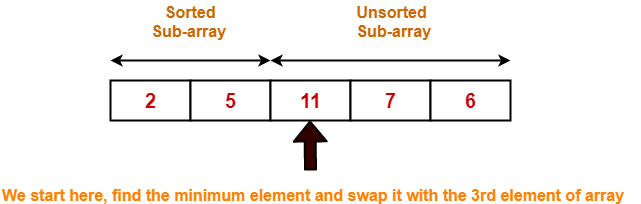
Step-04: For i = 3

 

 

Step-05: For i = 4

 

Loop gets terminated as ‘i’ becomes 4.

 

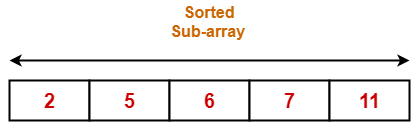
The state of array after the loops are finished is as shown-

 

 

With each loop cycle,

• The minimum element in unsorted sub-array is selected.
• It is then placed at the correct location in the sorted sub-array until array A is completely sorted.

 

Time Complexity Analysis-

 

• Selection sort algorithm consists of two nested loops.
• Owing to the two nested loops, it has O(n²) time complexity.

 

	Time Complexity
Best Case	n2
Average Case	n2
Worst Case	n2

 

Space Complexity Analysis-

 

• Selection sort is an in-place algorithm.
• It performs all computation in the original array and no other array is used.
• Hence, the space complexity works out to be O(1).

 

Important Notes-

 

• Selection sort is not a very efficient algorithm when data sets are large.
• This is indicated by the average and worst case complexities.
• Selection sort uses minimum number of swap operations O(n) among all the sorting algorithms.

 

To gain better understanding about Selection Sort Algorithm,

Watch this Video Lecture

 

Next Article- Bubble Sort

 

Other Popular Sorting Algorithms-

 

• Insertion Sort | Examples
• Merge Sort | Examples
• Quick Sort | Examples
• Topological Sort | Examples

 

Get more notes and other study material of Design and Analysis of Algorithms.

Watch video lectures by visiting our YouTube channel LearnVidFun.