Insertion Sort Algorithm | Example | Time Complexity

Insertion Sort-

 

• Insertion sort is an in-place sorting algorithm.
• It uses no auxiliary data structures while sorting.
• It is inspired from the way in which we sort playing cards.

 

How Insertion Sort Works?

 

Consider the following elements are to be sorted in ascending order-

6, 2, 11, 7, 5

 

Insertion sort works as-

 

Firstly,

• It selects the second element (2).
• It checks whether it is smaller than any of the elements before it.
• Since 2 < 6, so it shifts 6 towards right and places 2 before it.
• The resulting list is 2, 6, 11, 7, 5.

 

Secondly,

• It selects the third element (11).
• It checks whether it is smaller than any of the elements before it.
• Since 11 > (2, 6), so no shifting takes place.
• The resulting list remains the same.

 

Thirdly,

• It selects the fourth element (7).
• It checks whether it is smaller than any of the elements before it.
• Since 7 < 11, so it shifts 11 towards right and places 7 before it.
• The resulting list is 2, 6, 7, 11, 5.

 

Fourthly,

• It selects the fifth element (5).
• It checks whether it is smaller than any of the elements before it.
• Since 5 < (6, 7, 11), so it shifts (6, 7, 11) towards right and places 5 before them.
• The resulting list is 2, 5, 6, 7, 11.

 

As a result, sorted elements in ascending order are-

2, 5, 6, 7, 11

 

Insertion Sort Algorithm-

 

Let A be an array with n elements. The insertion sort algorithm used for sorting is as follows-

 

for (i = 1 ; i < n ; i++)

{

   key = A [ i ];

   j = i - 1;

   while(j > 0 && A [ j ] > key)

   {

       A [ j+1 ] = A [ j ];

       j--;

    }

    A [ j+1 ] = key;

}

 

Here,

• i = variable to traverse the array A
• key = variable to store the new number to be inserted into the sorted sub-array
• j = variable to traverse the sorted sub-array

 

Insertion Sort Example-

 

Consider the following elements are to be sorted in ascending order-

6, 2, 11, 7, 5

 

The above insertion sort algorithm works as illustrated below-

 

Step-01: For i = 1

 

 

Step-02: For i = 2

 

 

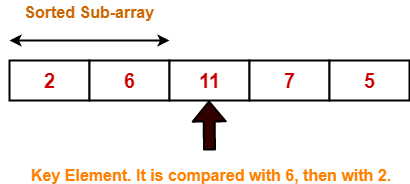
Step-03: For i = 3

 

 

2	5	11	7	6		For j = 2; 11 > 7 so A[3] = 11
2	5	11	11	6		For j = 1; 5 < 7 so loop stops and A[2] = 7
2	5	7	11	6		After inner loop ends

 

Working of inner loop when i = 3

 

Step-04: For i = 4

 

 

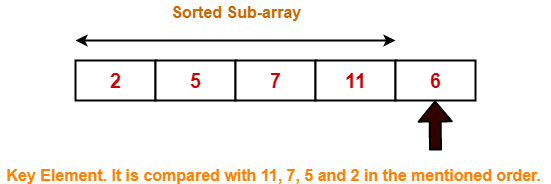
Loop gets terminated as ‘i’ becomes 5. The state of array after the loops are finished-

 

 

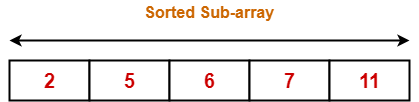
With each loop cycle,

• One element is placed at the correct location in the sorted sub-array until array A is completely sorted.

 

Time Complexity Analysis-

 

• Selection sort algorithm consists of two nested loops.
• Owing to the two nested loops, it has O(n²) time complexity.

 

	Time Complexity
Best Case	n
Average Case	n2
Worst Case	n2

 

Space Complexity Analysis-

 

• Selection sort is an in-place algorithm.
• It performs all computation in the original array and no other array is used.
• Hence, the space complexity works out to be O(1).

 

Important Notes-

 

• Insertion sort is not a very efficient algorithm when data sets are large.
• This is indicated by the average and worst case complexities.
• Insertion sort is adaptive and number of comparisons are less if array is partially sorted.

 

To gain better understanding about Insertion Sort Algorithm,

Watch this Video Lecture

 

Next Article- Merge Sort

 

Other Popular Sorting Algorithms-

 

• Selection Sort | Examples
• Bubble Sort | Examples
• Quick Sort | Examples
• Topological Sort | Examples

 

Get more notes and other study material of Design and Analysis of Algorithms.

Watch video lectures by visiting our YouTube channel LearnVidFun.