Quick Sort-
- Quick Sort is a famous sorting algorithm.
- It sorts the given data items in ascending order.
- It uses the idea of divide and conquer approach.
- It follows a recursive algorithm.
Quick Sort Algorithm-
Consider-
- a = Linear Array in memory
- beg = Lower bound of the sub array in question
- end = Upper bound of the sub array in question
Then, Quick Sort Algorithm is as follows-
Partition_Array (a , beg , end , loc)
Begin
Set left = beg , right = end , loc = beg
Set done = false
While (not done) do
While ( (a[loc] <= a[right] ) and (loc ≠ right) ) do
Set right = right - 1
end while
if (loc = right) then
Set done = true
else if (a[loc] > a[right]) then
Interchange a[loc] and a[right]
Set loc = right
end if
if (not done) then
While ( (a[loc] >= a[left] ) and (loc ≠ left) ) do
Set left = left + 1
end while
if (loc = left) then
Set done = true
else if (a[loc] < a[left]) then
Interchange a[loc] and a[left]
Set loc = left
end if
end if
end while
End
How Does Quick Sort Works?
- Quick Sort follows a recursive algorithm.
- It divides the given array into two sections using a partitioning element called as pivot.
The division performed is such that-
- All the elements to the left side of pivot are smaller than pivot.
- All the elements to the right side of pivot are greater than pivot.
After dividing the array into two sections, the pivot is set at its correct position.
Then, sub arrays are sorted separately by applying quick sort algorithm recursively.
Quick Sort Example-
Consider the following array has to be sorted in ascending order using quick sort algorithm-

Quick Sort Algorithm works in the following steps-
Step-01:
Initially-
- Left and Loc (pivot) points to the first element of the array.
- Right points to the last element of the array.
So to begin with, we set loc = 0, left = 0 and right = 5 as-
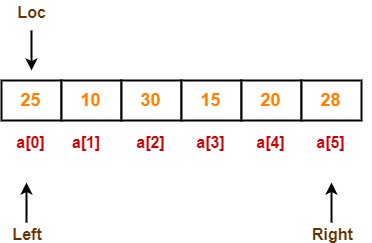
Step-02:
Since loc points at left, so algorithm starts from right and move towards left.
As a[loc] < a[right], so algorithm moves right one position towards left as-
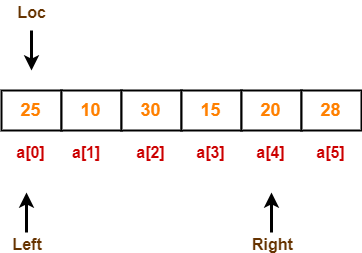
Now, loc = 0, left = 0 and right = 4.
Step-03:
Since loc points at left, so algorithm starts from right and move towards left.
As a[loc] > a[right], so algorithm swaps a[loc] and a[right] and loc points at right as-
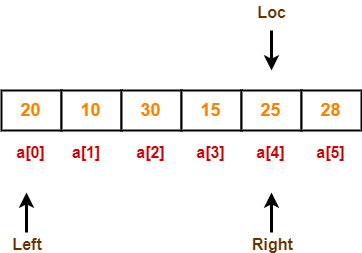
Now, loc = 4, left = 0 and right = 4.
Step-04:
Since loc points at right, so algorithm starts from left and move towards right.
As a[loc] > a[left], so algorithm moves left one position towards right as-
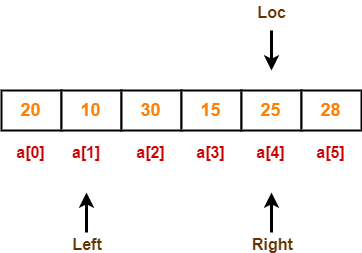
Now, loc = 4, left = 1 and right = 4.
Step-05:
Since loc points at right, so algorithm starts from left and move towards right.
As a[loc] > a[left], so algorithm moves left one position towards right as-
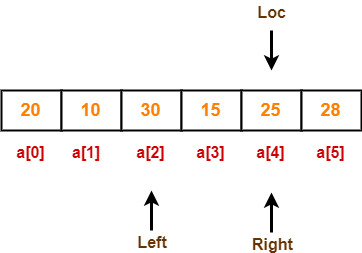
Now, loc = 4, left = 2 and right = 4.
Step-06:
Since loc points at right, so algorithm starts from left and move towards right.
As a[loc] < a[left], so we algorithm swaps a[loc] and a[left] and loc points at left as-
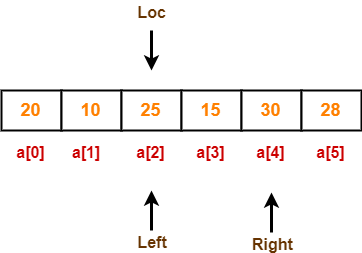
Now, loc = 2, left = 2 and right = 4.
Step-07:
Since loc points at left, so algorithm starts from right and move towards left.
As a[loc] < a[right], so algorithm moves right one position towards left as-

Now, loc = 2, left = 2 and right = 3.
Step-08:
Since loc points at left, so algorithm starts from right and move towards left.
As a[loc] > a[right], so algorithm swaps a[loc] and a[right] and loc points at right as-
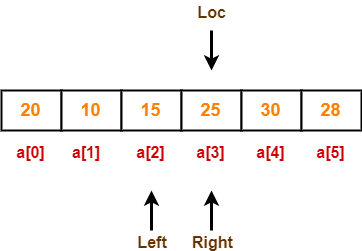
Now, loc = 3, left = 2 and right = 3.
Step-09:
Since loc points at right, so algorithm starts from left and move towards right.
As a[loc] > a[left], so algorithm moves left one position towards right as-
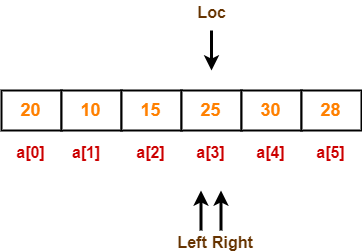
Now, loc = 3, left = 3 and right = 3.
Now,
- loc, left and right points at the same element.
- This indicates the termination of procedure.
- The pivot element 25 is placed in its final position.
- All elements to the right side of element 25 are greater than it.
- All elements to the left side of element 25 are smaller than it.

Now, quick sort algorithm is applied on the left and right sub arrays separately in the similar manner.
Quick Sort Analysis-
- To find the location of an element that splits the array into two parts, O(n) operations are required.
- This is because every element in the array is compared to the partitioning element.
- After the division, each section is examined separately.
- If the array is split approximately in half (which is not usually), then there will be log2n splits.
- Therefore, total comparisons required are f(n) = n x log2n = O(nlog2n).
| Order of Quick Sort = O(nlog2n) |
Worst Case-
- Quick Sort is sensitive to the order of input data.
- It gives the worst performance when elements are already in the ascending order.
- It then divides the array into sections of 1 and (n-1) elements in each call.
- Then, there are (n-1) divisions in all.
- Therefore, here total comparisons required are f(n) = n x (n-1) = O(n2).
| Order of Quick Sort in worst case = O(n2) |
Advantages of Quick Sort-
The advantages of quick sort algorithm are-
- Quick Sort is an in-place sort, so it requires no temporary memory.
- Quick Sort is typically faster than other algorithms.
(because its inner loop can be efficiently implemented on most architectures)
- Quick Sort tends to make excellent usage of the memory hierarchy like virtual memory or caches.
- Quick Sort can be easily parallelized due to its divide and conquer nature.
Disadvantages of Quick Sort-
The disadvantages of quick sort algorithm are-
- The worst case complexity of quick sort is O(n2).
- This complexity is worse than O(nlogn) worst case complexity of algorithms like merge sort, heap sort etc.
- It is not a stable sort i.e. the order of equal elements may not be preserved.
To gain better understanding about Quick Sort Algorithm,
Next Article- Topological Sort
Other Popular Sorting Algorithms-
Get more notes and other study material of Design and Analysis of Algorithms.
Watch video lectures by visiting our YouTube channel LearnVidFun.

