Tag: Theory of Computation Gate Notes

DFA to Regular Expression | Arden’s Theorem

Theory of Automata & Computation

DFA to Regular Expression-

 

The two popular methods for converting a given DFA to its regular expression are-

 

 

  1. Arden’s Method
  2. State Elimination Method

 

In this article, we will discuss Arden’s Theorem.

 

Arden’s Theorem-

 

Arden’s Theorem is popularly used to convert a given DFA to its regular expression.

 

It states that-

Let P and Q be two regular expressions over ∑.

If P does not contain a null string ∈, then-

R = Q + RP has a unique solution i.e. R = QP*

 

Conditions-

 

To use Arden’s Theorem, following conditions must be satisfied-

  • The transition diagram must not have any ∈ transitions.
  • There must be only a single initial state.

 

Steps-

 

To convert a given DFA to its regular expression using Arden’s Theorem, following steps are followed-

 

Step-01:

 

  • Form a equation for each state considering the transitions which comes towards that state.
  • Add ‘∈’ in the equation of initial state.

 

Step-02:

 

Bring final state in the form R = Q + RP to get the required regular expression.

 

Important Notes-

 

Note-01:

 

Arden’s Theorem can be used to find a regular expression for both DFA and NFA.

 

Note-02:

 

If there exists multiple final states, then-

  • Write a regular expression for each final state separately.
  • Add all the regular expressions to get the final regular expression.

 

Also Read- State Elimination Method

 

PRACTICE PROBLEMS BASED ON CONVERTING DFA TO REGULAR EXPRESSION-

 

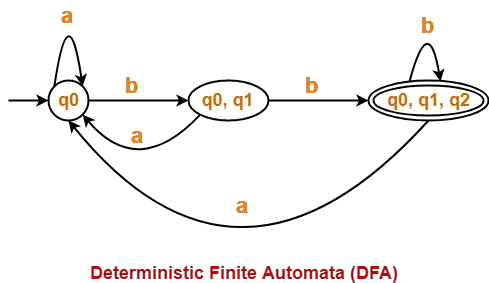
Problem-01:

 

Find regular expression for the following DFA using Arden’s Theorem-

 

 

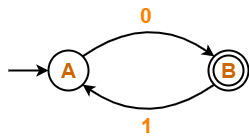
Solution-

 

Step-01:

 

Form a equation for each state-

  • A = ∈ + B.1     ……(1)
  • B = A.0           ……(2)

 

Step-02:

 

Bring final state in the form R = Q + RP.

 

Using (1) in (2), we get-

B = (∈ + B.1).0

B = ∈.0 + B.1.0

B = 0 + B.(1.0)          ……(3)

 

Using Arden’s Theorem in (3), we get-

B = 0.(1.0)*

 

Thus, Regular Expression for the given DFA = 0(10)*

 

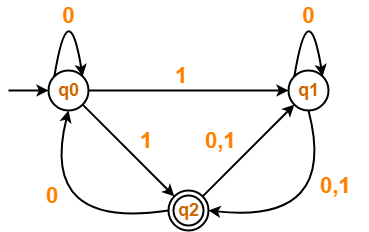
Problem-02:

 

Find regular expression for the following DFA using Arden’s Theorem-

 

 

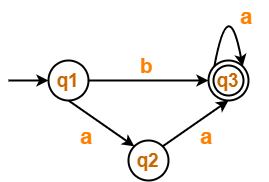
Solution-

 

Step-01:

 

Form a equation for each state-

  • q1 = ∈                                        ……(1)
  • q2 = q1.a                                   ……(2)
  • q3 = q1.b + q2.a + q3.a            …….(3)

 

Step-02:

 

Bring final state in the form R = Q + RP.

 

Using (1) in (2), we get-

q2 = ∈.a

q2 = a              …….(4)

 

Using (1) and (4) in (3), we get-

 

q3 = q1.b + q2.a + q3.a

q3 = ∈.b + a.a + q3.a

q3 = (b + a.a) + q3.a        …….(5)

 

Using Arden’s Theorem in (5), we get-

q3 = (b + a.a)a*

 

Thus, Regular Expression for the given DFA = (b + aa)a*

 

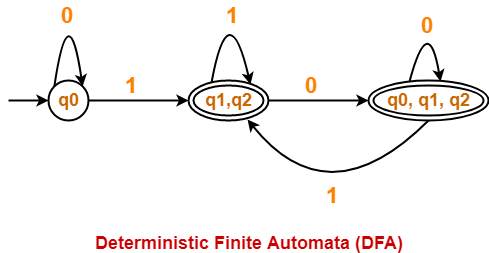
Problem-03:

 

Find regular expression for the following DFA using Arden’s Theorem-

 

 

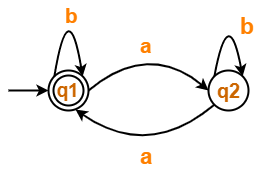
Solution-

 

Step-01:

 

Form a equation for each state-

  • q1 = ∈ + q1.b + q2.a                 ……(1)
  • q2 = q1.a + q2.b                       ……(2)

 

Step-02:

 

Bring final state in the form R = Q + RP.

 

Using Arden’s Theorem in (2), we get-

q2 = q1.a.b*             …….(3)

 

Using (3) in (1), we get-

q1 = ∈ + q1.b + q1.a.b*.a

q1 = ∈ + q1.(b + a.b*.a)          …….(4)

 

Using Arden’s Theorem in (4), we get-

q1 = ∈.(b + a.b*.a)*

q1 = (b + a.b*.a)*

 

Thus, Regular Expression for the given DFA = (b + a.b*.a)*

 

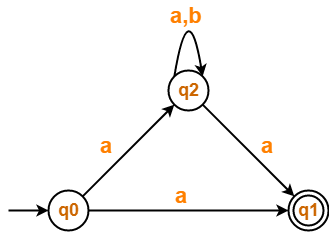
Problem-04:

 

Find regular expression for the following DFA using Arden’s Theorem-

 

 

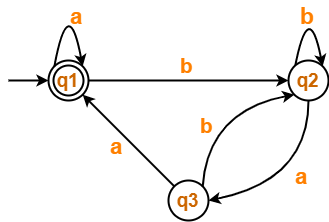
Solution-

 

Step-01:

 

Form a equation for each state-

  • q1 = ∈ + q1.a + q3.a                 ……(1)
  • q2 = q1.b + q2.b + q3.b            ……(2)
  • q3 = q2.a                                  …….(3)

 

Step-02:

 

Bring final state in the form R = Q + RP.

 

Using (3) in (2), we get-

q2 = q1.b + q2.b + q2.a.b

q2 = q1.b + q2.(b + a.b)          …….(4)

 

Using Arden’s Theorem in (4), we get-

q2 = q1.b.(b + a.b)*    …….(5)

 

Using (5) in (3), we get-

q3 = q1.b.(b + a.b)*.a       …….(6)

 

Using (6) in (1), we get-

q1 = ∈ + q1.a + q1.b.(b + a.b)*.a.a

q1 = ∈ + q1.(a + b.(b + a.b)*.a.a)        …….(7)

 

Using Arden’s Theorem in (7), we get-

q1 = ∈.(a + b.(b + a.b)*.a.a)*

q1 = (a + b.(b + a.b)*.a.a)*

 

Thus, Regular Expression for the given DFA = (a + b(b + ab)*aa)*

 

Also Read- Minimization of DFA

 

To gain better understanding about Arden’s Theorem,

Watch this Video Lecture

 

Next Article- Non-Deterministic Finite Automata

 

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Converting NFA to DFA | Solved Examples

Theory of Automata & Computation

Non-Deterministic Finite Automata-

 

Before you go through this article, make sure that you have gone through the previous article on Non-Deterministic Finite Automata.

 

In Non-Deterministic Finite Automata,

  • For some current state and input symbol, there exists more than one next output states.
  • A string is accepted only if there exists at least one transition path starting at initial state and ending at final state.

 

In this article, we will discuss how to convert a given NFA to a DFA.

 

Converting NFA to DFA-

 

The following steps are followed to convert a given NFA to a DFA-

 

Step-01:

 

  • Let Q’ be a new set of states of the DFA. Q’ is null in the starting.
  • Let T’ be a new transition table of the DFA.

 

Step-02:

 

  • Add start state of the NFA to Q’.
  • Add transitions of the start state to the transition table T’.
  • If start state makes transition to multiple states for some input alphabet, then treat those multiple states as a single state in the DFA.

 

In NFA, if the transition of start state over some input alphabet is null,

then perform the transition of start state over that input alphabet to a dead state in the DFA.

 

Step-03:

 

If any new state is present in the transition table T’,

  • Add the new state in Q’.
  • Add transitions of that state in the transition table T’.

 

Step-04:

 

Keep repeating Step-03 until no new state is present in the transition table T’.

Finally, the transition table T’ so obtained is the complete transition table of the required DFA.

 

PRACTICE PROBLEMS BASED ON CONVERTING NFA TO DFA-

 

Problem-01:

 

Convert the following Non-Deterministic Finite Automata (NFA) to Deterministic Finite Automata (DFA)-

 

 

Solution-

 

Transition table for the given Non-Deterministic Finite Automata (NFA) is-

 

State / Alphabet a b
→q0 q0 q0, q1
q1 – *q2
*q2 – –

 

Step-01:

 

Let Q’ be a new set of states of the Deterministic Finite Automata (DFA).

Let T’ be a new transition table of the DFA.

 

Step-02:

 

Add transitions of start state q0 to the transition table T’.

 

State / Alphabet a b
→q0 q0 {q0, q1}

 

Step-03:

 

New state present in state Q’ is {q0, q1}.

Add transitions for set of states {q0, q1} to the transition table T’.

 

State / Alphabet a b
→q0 q0 {q0, q1}
{q0, q1} q0 {q0, q1, q2}

 

Step-04:

 

New state present in state Q’ is {q0, q1, q2}.

Add transitions for set of states {q0, q1, q2} to the transition table T’.

 

State / Alphabet a b
→q0 q0 {q0, q1}
{q0, q1} q0 {q0, q1, q2}
{q0, q1, q2} q0 {q0, q1, q2}

 

Step-05:

 

Since no new states are left to be added in the transition table T’, so we stop.

States containing q2 as its component are treated as final states of the DFA.

 

Finally, Transition table for Deterministic Finite Automata (DFA) is-

 

State / Alphabet a b
→q0 q0 {q0, q1}
{q0, q1} q0 *{q0, q1, q2}
*{q0, q1, q2} q0 *{q0, q1, q2}

 

Now, Deterministic Finite Automata (DFA) may be drawn as-

 

 

Problem-02:

 

Convert the following Non-Deterministic Finite Automata (NFA) to Deterministic Finite Automata (DFA)-

 

 

Solution-

 

Transition table for the given Non-Deterministic Finite Automata (NFA) is-

 

State / Alphabet 0 1
→q0 q0 q1, *q2
q1 q1, *q2 *q2
*q2 q0, q1 q1

 

Step-01:

 

Let Q’ be a new set of states of the Deterministic Finite Automata (DFA).

Let T’ be a new transition table of the DFA.

 

Step-02:

 

Add transitions of start state q0 to the transition table T’.

 

State / Alphabet 0 1
→q0 q0 {q1, q2}

 

Step-03:

 

New state present in state Q’ is {q1, q2}.

Add transitions for set of states {q1, q2} to the transition table T’.

 

State / Alphabet 0 1
→q0 q0 {q1, q2}
{q1, q2} {q0, q1, q2} {q1, q2}

 

Step-04:

 

New state present in state Q’ is {q0, q1, q2}.

Add transitions for set of states {q0, q1, q2} to the transition table T’.

 

State / Alphabet 0 1
→q0 q0 {q1, q2}
{q1, q2} {q0, q1, q2} {q1, q2}
{q0, q1, q2} {q0, q1, q2} {q1, q2}

 

Step-05:

 

Since no new states are left to be added in the transition table T’, so we stop.

States containing q2 as its component are treated as final states of the DFA.

 

Finally, Transition table for Deterministic Finite Automata (DFA) is-

 

State / Alphabet 0 1
→q0 q0 *{q1, q2}
*{q1, q2} *{q0, q1, q2} *{q1, q2}
*{q0, q1, q2} *{q0, q1, q2} *{q1, q2}

 

Now, Deterministic Finite Automata (DFA) may be drawn as-

 

 

Problem-03:

 

Convert the following Non-Deterministic Finite Automata (NFA) to Deterministic Finite Automata (DFA)-

 

 

Solution-

 

Transition table for the given Non-Deterministic Finite Automata (NFA) is-

 

State / Alphabet a b
→q0 *q1, q2 –
*q1 – –
q2 *q1, q2 q2

 

Step-01:

 

Let Q’ be a new set of states of the Deterministic Finite Automata (DFA).

Let T’ be a new transition table of the DFA.

 

Step-02:

 

Add transitions of start state q0 to the transition table T’.

 

State / Alphabet a b
→q0 {q1, q2} Ø (Dead State)

 

Step-03:

 

New state present in state Q’ is {q1, q2}.

Add transitions for set of states {q1, q2} to the transition table T’.

 

State / Alphabet a b
→q0 {q1, q2} Ø
{q1, q2} {q1, q2} q2

 

Step-04:

 

New state present in state Q’ is q2.

Add transitions for state q2 to the transition table T’.

 

State / Alphabet a b
→q0 {q1, q2} Ø
{q1, q2} {q1, q2} q2
q2 {q1, q2} q2

 

Step-05:

 

Add transitions for dead state {Ø} to the transition table T’.

 

State / Alphabet a b
→q0 {q1, q2} Ø
{q1, q2} {q1, q2} q2
q2 {q1, q2} q2
Ø Ø Ø

 

Step-06:

 

Since no new states are left to be added in the transition table T’, so we stop.

States containing q1 as its component are treated as final states of the DFA.

 

Finally, Transition table for Deterministic Finite Automata (DFA) is-

 

State / Alphabet a b
→q0 *{q1, q2} Ø
*{q1, q2} *{q1, q2} q2
q2 *{q1, q2} q2
Ø Ø Ø

 

Now, Deterministic Finite Automata (DFA) may be drawn as-

 

 

Important Points-

 

It is important to note the following points when converting a given NFA into a DFA-

 

Note-01:

 

  • After conversion, the number of states in the resulting DFA may or may not be same as NFA.
  • The maximum number of states that may be present in the DFA are 2Number of states in the NFA.

 

Note-02:

 

In general, the following relationship exists between the number of states in the NFA and DFA-

 

1 <= n <= 2m

 

Here,

  • n = Number of states in the DFA
  • m = Number of states in the NFA

 

Note-03:

 

  • In the resulting DFA, all those states that contain the final state(s) of NFA are treated as final states.

 

To gain better understanding about Converting NFA to DFA,

Watch this Video Lecture

 

Next Article- Parse Tree | Derivations

 

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Non Deterministic Finite Automata | NFA

Theory of Automata & Computation

Non-Deterministic Finite Automata-

 

Non-Deterministic Finite Automata (NDFA / NFA) is an automata in which

for some current state and input symbol, there exists more than one next output states.

 

It is also known as Non-Deterministic Finite Accepter (NFA).

 

Formal Definition-

 

Non-Deterministic Finite Automata is defined by the quintuple-

M = (Q, ∑, δ, q0, F)

 

where-

  • Q = finite set of states
  • ∑ = non-empty finite set of symbols called as input alphabets
  • δ : Q x ∑ → 2Q is a total function called as transition function
  • q0 ∈ Q is the initial state
  • F ⊆ Q is a set of final states

 

Example of Non-Deterministic Finite Automata Without Epsilon-

 

Following automata is an example of Non-Deterministic Finite Automata without epsilon-

 

 

The above NFA can be defined in form of five tuples as-

{ {A, B, C, D, E, F}, {a, b, c}, δ, A, {D, F} }

 

where-

  • {A, B, C, D, E, F} refers to the set of states
  • {a, b, c} refers to the set of input alphabets
  • δ refers to the transition function
  • A refers to the the initial state
  • {D, F} refers to the set of final states

 

Transition function δ is defined as-

  • δ (A, a) = B
  • δ (A, a) = E
  • δ (B, b) = C
  • δ (C, c) = D
  • δ (E, b) = F
  • δ (F, c) = E

 

Transition Table for the above Non-Deterministic Finite Automata is-

 

States / Alphabets a b c
A {B, F} – –
B – C –
C – – D
D – – –
E – F –
F – – E

 

Example of Non-Deterministic Finite Automata With Epsilon-

 

Following automata is an example of Non-Deterministic Finite Automata with epsilon-

 

 

The above NFA can be defined in form of five tuples as-

{ {A, B, C}, {0, 1}, δ, A, {A} }

 

where-

  • {A, B, C} refers to the set of states
  • {0, 1} refers to the set of input alphabets
  • δ refers to the transition function
  • A refers to the the initial state
  • {A} refers to the set of final states

 

Transition function δ is defined as-

  • δ (A, 1) = B
  • δ (A, ∈) = C
  • δ (B, 0) = A
  • δ (B, 0) = C
  • δ (B, 1) = C

 

Transition Table for the above Non-Deterministic Finite Automata is-

 

States / Alphabets 0 1 ∈
A – B C
B {A, C} C –
C – – –

 

Dead Configuration or Trap State-

 

In Non-Deterministic Finite Automata,

  • The result of a transition function may be empty.
  • In such a case, automata gets stopped forcefully after entering that configuration.
  • This type of configuration is known as dead configuration.
  • The string gets rejected after entering the dead configuration.

 

Equivalence of DFA and NFA-

 

Two finite accepters are said to be equal in power if they both accepts the same language.

DFA and NFA are both exactly equal in power.

 

Example-

 

Consider a language L(M) = { (10)n : n >= 0 }

 

Equivalent NFA for the language L(M) is-

 

 

Equivalent DFA for the language L(M) is-

 

 

  • Both the above automata accepts the same language L(M).
  • Thus, both are equal in power.

 

Important Points

 

It is important to note the following points-

  • Both DFA and NFA are exactly same in power.
  • For any regular language, both DFA and NFA can be constructed.
  • There exists an equivalent DFA corresponding to every NFA.
  • Every NFA can be converted into its equivalent DFA.
  • There exists no NFA that can not be converted into its equivalent DFA.
  • Every DFA is a NFA but every NFA is not a DFA.

 

Acceptance by NFA-

 

A string ‘w’ is said to be accepted by a NFA if

there exists at least one transition path on which we start at initial state and ends at final state.

δ* (q0, w) = F

 

Example-

 

Consider the following NFA-

 

 

For the string w = ab,

  • There exists two transition paths.
  • One transition path starts at initial state and ends at final state.
  • Therefore, string w = ab is accepted by the NFA.

 

To gain better understanding about Non-Deterministic Finite Automata,

Watch this Video Lecture

 

Next Article- Converting NFA to DFA

 

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Ambiguous Grammar | Parse Tree | Important Points

Theory of Automata & Computation

Ambiguous Grammar & Parse Tree-

 

We have discussed-

  • Ambiguous Grammar generates at least one string that has more than one parse tree.
  • Parse Tree is the geometrical representation of a derivation.

 

In this article, we will discuss important points about Ambiguous Grammar and Parse Tree.

 

Important Points-

 

Point-01:

 

  • There always exists a unique parse tree corresponding to each leftmost derivation and rightmost derivation.

 

If n parse trees exist for any string w, then there will be-

  • n corresponding leftmost derivations.
  • n corresponding rightmost derivations.

 

Point-02:

 

For ambiguous grammars,

  • More than one leftmost derivation and more than one rightmost derivation exist for at least one string.
  • Leftmost derivation and rightmost derivation represents different parse trees.

 

Point-03:

 

For unambiguous grammars,

  • A unique leftmost derivation and a unique rightmost derivation exist for all the strings.
  • Leftmost derivation and rightmost derivation represents the same parse tree.

 

Point-04:

 

  • There may exist derivations for a string which are neither leftmost nor rightmost.

 

Example

 

Consider the following grammar-

S → ABC

A → a

B → b

C → c

 

Consider a string w = abc.

Total 6 derivations exist for string w.

The following 4 derivations are neither leftmost nor rightmost-

 

Derivation-01:

 

S → ABC

→ aBC    (Using A → a)

→ aBc     (Using C → c)

→ abc     (Using B → b)

 

Derivation-02:

 

S → ABC

→ AbC    (Using B → b)

→ abC     (Using A → a)

→ abc     (Using C → c)

 

Derivation-03:

 

S → ABC

→ AbC    (Using B → b)

→ Abc     (Using C → c)

→ abc     (Using A → a)

 

The other 2 derivations are leftmost derivation and rightmost derivation.

 

Point-05:

 

  • Leftmost derivation and rightmost derivation of a string may be exactly same.
  • In fact, there may exist a grammar in which leftmost derivation and rightmost derivation is exactly same for all the strings.

 

Example

 

Consider the following grammar-

S → aS / ∈

 

The language generated by this grammar is-

L = { an , n>=0 } or a*

 

All the strings generated from this grammar have their leftmost derivation and rightmost derivation exactly same.

Let us consider a string w = aaa.

 

Leftmost Derivation-

 

S → aS

→ aaS       (Using S → aS)

→ aaaS     (Using S → aS)

→ aaa∈

→ aaa

 

Rightmost Derivation-

 

S → aS

→ aaS       (Using S → aS)

→ aaaS     (Using S → aS)

→ aaa∈

→ aaa

 

Clearly,

Leftmost derivation = Rightmost derivation

Similar is the case for all other strings.

 

Point-06:

 

  • For a given parse tree, we may have its leftmost derivation exactly same as rightmost derivation.

 

Point-07:

 

  • If for all the strings of a grammar, leftmost derivation is exactly same as rightmost derivation, then that grammar may be ambiguous or unambiguous.

 

Example

 

Consider the following grammar-

S → aS / ∈

  • This is an example of an unambiguous grammar.
  • Here, each string have its leftmost derivation and rightmost derivation exactly same.

 

Now, consider the following grammar-

S → aS / a / ∈

  • This is an example of ambiguous grammar.
  • Here also, each string have its leftmost derivation and rightmost derivation exactly same.

 

Consider a string w = a.

 

 

Since two different parse trees exist, so grammar is ambiguous.

 

Leftmost derivation and rightmost derivation for parse tree-01 are-

S → a

 

Leftmost derivation and rightmost derivation for parse tree-02 are-

S → aS

S → a∈

S → a

 

Next Article- Language of Grammar

 

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Removing Ambiguity | Ambiguous to Unambiguous

Theory of Automata & Computation

Grammar Ambiguity-

 

Before you go through this article, make sure that you have gone through the previous article on Grammar Ambiguity.

 

We have discussed-

  • There exists no general algorithm to remove the ambiguity from grammar.
  • To check grammar ambiguity, we try finding a string that has more than one parse tree.
  • If any such string exists, then the grammar is ambiguous otherwise not.

 

In this article, we will discuss how to convert ambiguous grammar into unambiguous grammar.

 

Converting Ambiguous Grammar Into Unambiguous Grammar-

 

  • Causes such as left recursion, common prefixes etc makes the grammar ambiguous.
  • The removal of these causes may convert the grammar into unambiguous grammar.
  •  However, it is not always compulsory.

 

NOTE

It is not always possible to convert an ambiguous grammar into an unambiguous grammar.

 

Methods To Remove Ambiguity-

 

The ambiguity from the grammar may be removed using the following methods-

 

 

  • By fixing the grammar
  • By adding grouping rules
  • By using semantics and choosing the parse that makes the most sense
  • By adding the precedence rules or other context sensitive parsing rules

 

Removing Ambiguity By Precedence & Associativity Rules-

 

An ambiguous grammar may be converted into an unambiguous grammar by implementing-

  • Precedence Constraints
  • Associativity Constraints

 

These constraints are implemented using the following rules-

 

Rule-01:

 

The precedence constraint is implemented using the following rules-

  • The level at which the production is present defines the priority of the operator contained in it.
  • The higher the level of the production, the lower the priority of operator.
  • The lower the level of the production, the higher the priority of operator.

 

Rule-02:

 

The associativity constraint is implemented using the following rules-

  • If the operator is left associative, induce left recursion in its production.
  • If the operator is right associative, induce right recursion in its production.

 

PROBLEMS BASED ON CONVERSION INTO UNAMBIGUOUS GRAMMAR-

 

Problem-01:

 

Convert the following ambiguous grammar into unambiguous grammar-

R → R + R / R . R / R* / a / b

where * is kleen closure and . is concatenation.

 

Solution-

 

To convert the given grammar into its corresponding unambiguous grammar, we implement the precedence and associativity constraints.

 

We have-

  • Given grammar consists of the following operators-

+ , . , *

  • Given grammar consists of the following operands-

a , b

 

The priority order is-

(a , b) > * > . > +

where-

  • . operator is left associative
  • + operator is left associative

 

Using the precedence and associativity rules, we write the corresponding unambiguous grammar as-

 

E → E + T / T

T → T . F / F

F → F* / G

G → a / b

Unambiguous Grammar

 

OR

 

E → E + T / T

T → T . F / F

F → F* / a / b

Unambiguous Grammar

 

Problem-02:

 

Convert the following ambiguous grammar into unambiguous grammar-

bexp → bexp or bexp / bexp and bexp / not bexp / T / F

where bexp represents Boolean expression, T represents True and F represents False.

 

Solution-

 

To convert the given grammar into its corresponding unambiguous grammar, we implement the precedence and associativity constraints.

 

We have-

  • Given grammar consists of the following operators-

or , and , not

  • Given grammar consists of the following operands-

T , F

 

The priority order is-

(T , F) > not > and > or

where-

  • and operator is left associative
  • or operator is left associative

 

Using the precedence and associativity rules, we write the corresponding unambiguous grammar as-

 

bexp → bexp or M / M

M → M and N / N

N → not N / G

G → T / F

Unambiguous Grammar

 

OR

 

bexp → bexp or M / M

M → M and N / N

N → not N / T / F

Unambiguous Grammar

 

To gain better understanding about Conversion into Unambiguous Grammar-

Watch this Video Lecture

 

Next Article- Evaluating Expressions Based On Given Grammar

 

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.