Non Deterministic Finite Automata | NFA

Non-Deterministic Finite Automata-

 

Non-Deterministic Finite Automata (NDFA / NFA) is an automata in which for some current state and input symbol, there exists more than one next output states.

 

It is also known as Non-Deterministic Finite Accepter (NFA).

 

Formal Definition-

 

Non-Deterministic Finite Automata is defined by the quintuple-

M = (Q, ∑, δ, q₀, F)

 

where-

• Q = finite set of states
• ∑ = non-empty finite set of symbols called as input alphabets
• δ : Q x ∑ → 2^Q is a total function called as transition function
• q0 ∈ Q is the initial state
• F ⊆ Q is a set of final states

 

Example of Non-Deterministic Finite Automata Without Epsilon-

 

Following automata is an example of Non-Deterministic Finite Automata without epsilon-

 

 

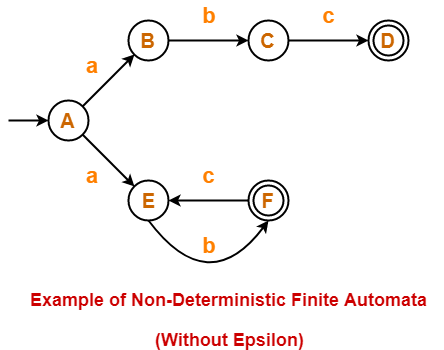
The above NFA can be defined in form of five tuples as-

{ {A, B, C, D, E, F}, {a, b, c}, δ, A, {D, F} }

 

where-

• {A, B, C, D, E, F} refers to the set of states
• {a, b, c} refers to the set of input alphabets
• δ refers to the transition function
• A refers to the the initial state
• {D, F} refers to the set of final states

 

Transition function δ is defined as-

• δ (A, a) = B
• δ (A, a) = E
• δ (B, b) = C
• δ (C, c) = D
• δ (E, b) = F
• δ (F, c) = E

 

Transition Table for the above Non-Deterministic Finite Automata is-

 

States / Alphabets	a	b	c
A	{B, F}	–	–
B	–	C	–
C	–	–	D
D	–	–	–
E	–	F	–
F	–	–	E

 

Example of Non-Deterministic Finite Automata With Epsilon-

 

Following automata is an example of Non-Deterministic Finite Automata with epsilon-

 

 

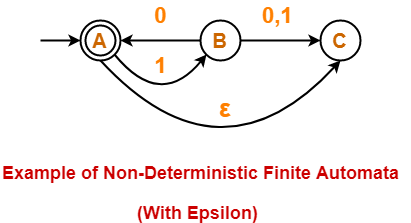
The above NFA can be defined in form of five tuples as-

{ {A, B, C}, {0, 1}, δ, A, {A} }

 

where-

• {A, B, C} refers to the set of states
• {0, 1} refers to the set of input alphabets
• δ refers to the transition function
• A refers to the the initial state
• {A} refers to the set of final states

 

Transition function δ is defined as-

• δ (A, 1) = B
• δ (A, ∈) = C
• δ (B, 0) = A
• δ (B, 0) = C
• δ (B, 1) = C

 

Transition Table for the above Non-Deterministic Finite Automata is-

 

States / Alphabets	0	1	∈
A	–	B	C
B	{A, C}	C	–
C	–	–	–

 

Dead Configuration or Trap State-

 

In Non-Deterministic Finite Automata,

• The result of a transition function may be empty.
• In such a case, automata gets stopped forcefully after entering that configuration.
• This type of configuration is known as dead configuration.
• The string gets rejected after entering the dead configuration.

 

Equivalence of DFA and NFA-

 

Two finite accepters are said to be equal in power if they both accepts the same language. DFA and NFA are both exactly equal in power.

 

Example-

 

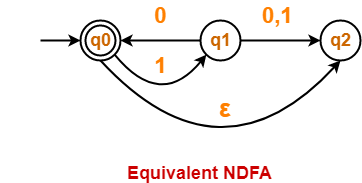
Consider a language L(M) = { (10)ⁿ : n >= 0 }

 

Equivalent NFA for the language L(M) is-

 

 

Equivalent DFA for the language L(M) is-

 

 

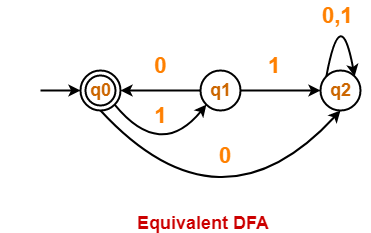
• Both the above automata accepts the same language L(M).
• Thus, both are equal in power.

 

Important Points   It is important to note the following points- Both DFA and NFA are exactly same in power. For any regular language, both DFA and NFA can be constructed. There exists an equivalent DFA corresponding to every NFA. Every NFA can be converted into its equivalent DFA. There exists no NFA that can not be converted into its equivalent DFA. Every DFA is a NFA but every NFA is not a DFA.

 

Acceptance by NFA-

 

A string ‘w’ is said to be accepted by a NFA if there exists at least one transition path on which we start at initial state and ends at final state. δ* (q0, w) = F

 

Example-

 

Consider the following NFA-

 

 

For the string w = ab,

• There exists two transition paths.
• One transition path starts at initial state and ends at final state.
• Therefore, string w = ab is accepted by the NFA.

 

To gain better understanding about Non-Deterministic Finite Automata,

Watch this Video Lecture

 

Next Article- Converting NFA to DFA

 

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.