Non-Deterministic Finite Automata-
Before you go through this article, make sure that you have gone through the previous article on Non-Deterministic Finite Automata.
In Non-Deterministic Finite Automata,
- For some current state and input symbol, there exists more than one next output states.
- A string is accepted only if there exists at least one transition path starting at initial state and ending at final state.
In this article, we will discuss how to convert a given NFA to a DFA.
Converting NFA to DFA-
The following steps are followed to convert a given NFA to a DFA-
Step-01:
- Let Q’ be a new set of states of the DFA. Q’ is null in the starting.
- Let T’ be a new transition table of the DFA.
Step-02:
- Add start state of the NFA to Q’.
- Add transitions of the start state to the transition table T’.
- If start state makes transition to multiple states for some input alphabet, then treat those multiple states as a single state in the DFA.
| In NFA, if the transition of start state over some input alphabet is null,
then perform the transition of start state over that input alphabet to a dead state in the DFA. |
Step-03:
If any new state is present in the transition table T’,
- Add the new state in Q’.
- Add transitions of that state in the transition table T’.
Step-04:
Keep repeating Step-03 until no new state is present in the transition table T’.
Finally, the transition table T’ so obtained is the complete transition table of the required DFA.
PRACTICE PROBLEMS BASED ON CONVERTING NFA TO DFA-
Problem-01:
Convert the following Non-Deterministic Finite Automata (NFA) to Deterministic Finite Automata (DFA)-

Solution-
Transition table for the given Non-Deterministic Finite Automata (NFA) is-
| State / Alphabet | a | b |
| →q0 | q0 | q0, q1 |
| q1 | – | *q2 |
| *q2 | – | – |
Step-01:
Let Q’ be a new set of states of the Deterministic Finite Automata (DFA).
Let T’ be a new transition table of the DFA.
Step-02:
Add transitions of start state q0 to the transition table T’.
| State / Alphabet | a | b |
| →q0 | q0 | {q0, q1} |
Step-03:
New state present in state Q’ is {q0, q1}.
Add transitions for set of states {q0, q1} to the transition table T’.
| State / Alphabet | a | b |
| →q0 | q0 | {q0, q1} |
| {q0, q1} | q0 | {q0, q1, q2} |
Step-04:
New state present in state Q’ is {q0, q1, q2}.
Add transitions for set of states {q0, q1, q2} to the transition table T’.
| State / Alphabet | a | b |
| →q0 | q0 | {q0, q1} |
| {q0, q1} | q0 | {q0, q1, q2} |
| {q0, q1, q2} | q0 | {q0, q1, q2} |
Step-05:
Since no new states are left to be added in the transition table T’, so we stop.
States containing q2 as its component are treated as final states of the DFA.
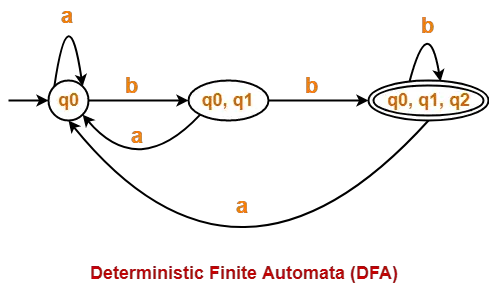
Finally, Transition table for Deterministic Finite Automata (DFA) is-
| State / Alphabet | a | b |
| →q0 | q0 | {q0, q1} |
| {q0, q1} | q0 | *{q0, q1, q2} |
| *{q0, q1, q2} | q0 | *{q0, q1, q2} |
Now, Deterministic Finite Automata (DFA) may be drawn as-
Problem-02:
Convert the following Non-Deterministic Finite Automata (NFA) to Deterministic Finite Automata (DFA)-
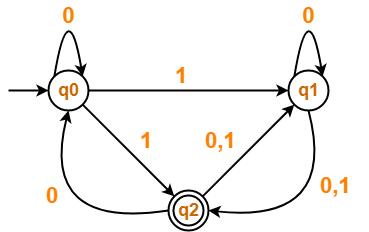
Solution-
Transition table for the given Non-Deterministic Finite Automata (NFA) is-
| State / Alphabet | 0 | 1 |
| →q0 | q0 | q1, *q2 |
| q1 | q1, *q2 | *q2 |
| *q2 | q0, q1 | q1 |
Step-01:
Let Q’ be a new set of states of the Deterministic Finite Automata (DFA).
Let T’ be a new transition table of the DFA.
Step-02:
Add transitions of start state q0 to the transition table T’.
| State / Alphabet | 0 | 1 |
| →q0 | q0 | {q1, q2} |
Step-03:
New state present in state Q’ is {q1, q2}.
Add transitions for set of states {q1, q2} to the transition table T’.
| State / Alphabet | 0 | 1 |
| →q0 | q0 | {q1, q2} |
| {q1, q2} | {q0, q1, q2} | {q1, q2} |
Step-04:
New state present in state Q’ is {q0, q1, q2}.
Add transitions for set of states {q0, q1, q2} to the transition table T’.
| State / Alphabet | 0 | 1 |
| →q0 | q0 | {q1, q2} |
| {q1, q2} | {q0, q1, q2} | {q1, q2} |
| {q0, q1, q2} | {q0, q1, q2} | {q1, q2} |
Step-05:
Since no new states are left to be added in the transition table T’, so we stop.
States containing q2 as its component are treated as final states of the DFA.
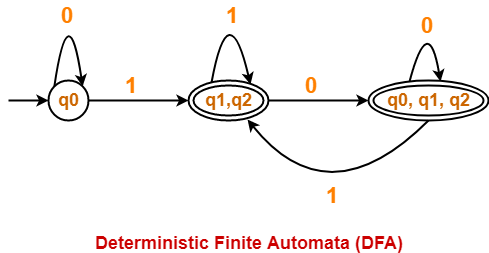
Finally, Transition table for Deterministic Finite Automata (DFA) is-
| State / Alphabet | 0 | 1 |
| →q0 | q0 | *{q1, q2} |
| *{q1, q2} | *{q0, q1, q2} | *{q1, q2} |
| *{q0, q1, q2} | *{q0, q1, q2} | *{q1, q2} |
Now, Deterministic Finite Automata (DFA) may be drawn as-
Problem-03:
Convert the following Non-Deterministic Finite Automata (NFA) to Deterministic Finite Automata (DFA)-
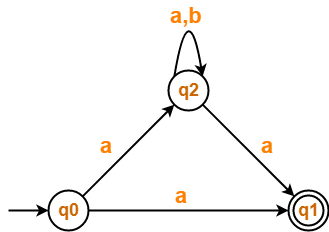
Solution-
Transition table for the given Non-Deterministic Finite Automata (NFA) is-
| State / Alphabet | a | b |
| →q0 | *q1, q2 | – |
| *q1 | – | – |
| q2 | *q1, q2 | q2 |
Step-01:
Let Q’ be a new set of states of the Deterministic Finite Automata (DFA).
Let T’ be a new transition table of the DFA.
Step-02:
Add transitions of start state q0 to the transition table T’.
| State / Alphabet | a | b |
| →q0 | {q1, q2} | Ø (Dead State) |
Step-03:
New state present in state Q’ is {q1, q2}.
Add transitions for set of states {q1, q2} to the transition table T’.
| State / Alphabet | a | b |
| →q0 | {q1, q2} | Ø |
| {q1, q2} | {q1, q2} | q2 |
Step-04:
New state present in state Q’ is q2.
Add transitions for state q2 to the transition table T’.
| State / Alphabet | a | b |
| →q0 | {q1, q2} | Ø |
| {q1, q2} | {q1, q2} | q2 |
| q2 | {q1, q2} | q2 |
Step-05:
Add transitions for dead state {Ø} to the transition table T’.
| State / Alphabet | a | b |
| →q0 | {q1, q2} | Ø |
| {q1, q2} | {q1, q2} | q2 |
| q2 | {q1, q2} | q2 |
| Ø | Ø | Ø |
Step-06:
Since no new states are left to be added in the transition table T’, so we stop.
States containing q1 as its component are treated as final states of the DFA.
Finally, Transition table for Deterministic Finite Automata (DFA) is-
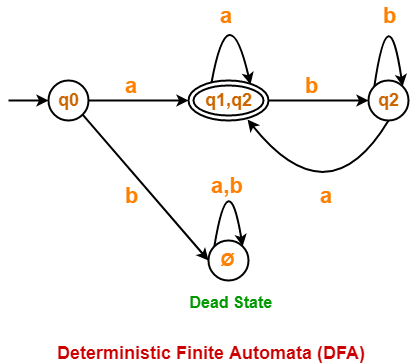
| State / Alphabet | a | b |
| →q0 | *{q1, q2} | Ø |
| *{q1, q2} | *{q1, q2} | q2 |
| q2 | *{q1, q2} | q2 |
| Ø | Ø | Ø |
Now, Deterministic Finite Automata (DFA) may be drawn as-
Important Points-
It is important to note the following points when converting a given NFA into a DFA-
Note-01:
- After conversion, the number of states in the resulting DFA may or may not be same as NFA.
- The maximum number of states that may be present in the DFA are 2Number of states in the NFA.
Note-02:
In general, the following relationship exists between the number of states in the NFA and DFA-
| 1 <= n <= 2m |
Here,
- n = Number of states in the DFA
- m = Number of states in the NFA
Note-03:
- In the resulting DFA, all those states that contain the final state(s) of NFA are treated as final states.
To gain better understanding about Converting NFA to DFA,
Next Article- Parse Tree | Derivations
Get more notes and other study material of Theory of Automata and Computation.
Watch video lectures by visiting our YouTube channel LearnVidFun.

