DFA to Regular Expression-
The two popular methods for converting a given DFA to its regular expression are-

- Arden’s Method
- State Elimination Method
In this article, we will discuss Arden’s Theorem.
Arden’s Theorem-
Arden’s Theorem is popularly used to convert a given DFA to its regular expression.
It states that-
Let P and Q be two regular expressions over ∑.
If P does not contain a null string ∈, then-
R = Q + RP has a unique solution i.e. R = QP*
Conditions-
To use Arden’s Theorem, following conditions must be satisfied-
- The transition diagram must not have any ∈ transitions.
- There must be only a single initial state.
Steps-
To convert a given DFA to its regular expression using Arden’s Theorem, following steps are followed-
Step-01:
- Form a equation for each state considering the transitions which comes towards that state.
- Add ‘∈’ in the equation of initial state.
Step-02:
Bring final state in the form R = Q + RP to get the required regular expression.
Important Notes-
Note-01:
Arden’s Theorem can be used to find a regular expression for both DFA and NFA.
Note-02:
If there exists multiple final states, then-
- Write a regular expression for each final state separately.
- Add all the regular expressions to get the final regular expression.
Also Read- State Elimination Method
PRACTICE PROBLEMS BASED ON CONVERTING DFA TO REGULAR EXPRESSION-
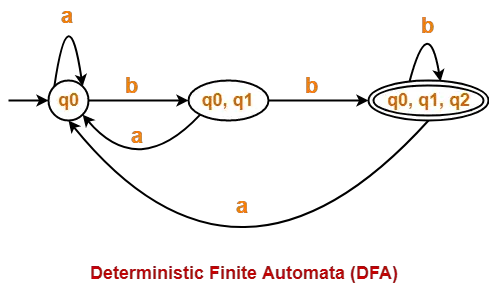
Problem-01:
Find regular expression for the following DFA using Arden’s Theorem-
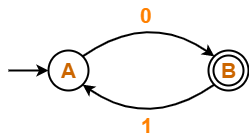
Solution-
Step-01:
Form a equation for each state-
- A = ∈ + B.1 ……(1)
- B = A.0 ……(2)
Step-02:
Bring final state in the form R = Q + RP.
Using (1) in (2), we get-
B = (∈ + B.1).0
B = ∈.0 + B.1.0
B = 0 + B.(1.0) ……(3)
Using Arden’s Theorem in (3), we get-
B = 0.(1.0)*
Thus, Regular Expression for the given DFA = 0(10)*
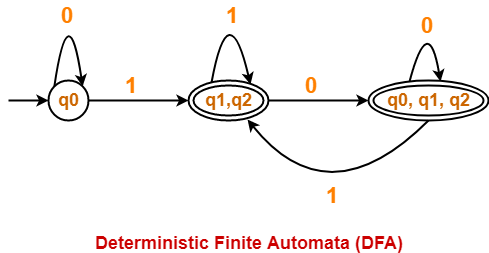
Problem-02:
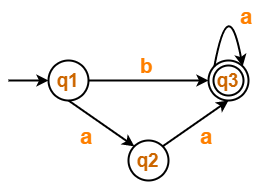
Find regular expression for the following DFA using Arden’s Theorem-
Solution-
Step-01:
Form a equation for each state-
- q1 = ∈ ……(1)
- q2 = q1.a ……(2)
- q3 = q1.b + q2.a + q3.a …….(3)
Step-02:
Bring final state in the form R = Q + RP.
Using (1) in (2), we get-
q2 = ∈.a
q2 = a …….(4)
Using (1) and (4) in (3), we get-
q3 = q1.b + q2.a + q3.a
q3 = ∈.b + a.a + q3.a
q3 = (b + a.a) + q3.a …….(5)
Using Arden’s Theorem in (5), we get-
q3 = (b + a.a)a*
Thus, Regular Expression for the given DFA = (b + aa)a*
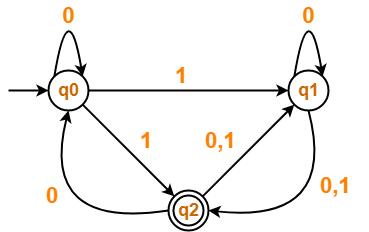
Problem-03:
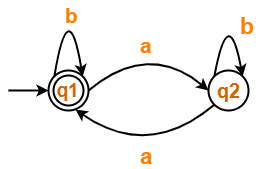
Find regular expression for the following DFA using Arden’s Theorem-
Solution-
Step-01:
Form a equation for each state-
- q1 = ∈ + q1.b + q2.a ……(1)
- q2 = q1.a + q2.b ……(2)
Step-02:
Bring final state in the form R = Q + RP.
Using Arden’s Theorem in (2), we get-
q2 = q1.a.b* …….(3)
Using (3) in (1), we get-
q1 = ∈ + q1.b + q1.a.b*.a
q1 = ∈ + q1.(b + a.b*.a) …….(4)
Using Arden’s Theorem in (4), we get-
q1 = ∈.(b + a.b*.a)*
q1 = (b + a.b*.a)*
Thus, Regular Expression for the given DFA = (b + a.b*.a)*
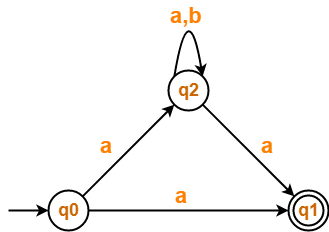
Problem-04:
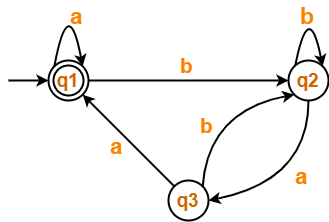
Find regular expression for the following DFA using Arden’s Theorem-
Solution-
Step-01:
Form a equation for each state-
- q1 = ∈ + q1.a + q3.a ……(1)
- q2 = q1.b + q2.b + q3.b ……(2)
- q3 = q2.a …….(3)
Step-02:
Bring final state in the form R = Q + RP.
Using (3) in (2), we get-
q2 = q1.b + q2.b + q2.a.b
q2 = q1.b + q2.(b + a.b) …….(4)
Using Arden’s Theorem in (4), we get-
q2 = q1.b.(b + a.b)* …….(5)
Using (5) in (3), we get-
q3 = q1.b.(b + a.b)*.a …….(6)
Using (6) in (1), we get-
q1 = ∈ + q1.a + q1.b.(b + a.b)*.a.a
q1 = ∈ + q1.(a + b.(b + a.b)*.a.a) …….(7)
Using Arden’s Theorem in (7), we get-
q1 = ∈.(a + b.(b + a.b)*.a.a)*
q1 = (a + b.(b + a.b)*.a.a)*
Thus, Regular Expression for the given DFA = (a + b(b + ab)*aa)*
Also Read- Minimization of DFA
To gain better understanding about Arden’s Theorem,
Next Article- Non-Deterministic Finite Automata
Get more notes and other study material of Theory of Automata and Computation.
Watch video lectures by visiting our YouTube channel LearnVidFun.