Topological Sort-
| Topological Sort is a linear ordering of the vertices in such a way that
if there is an edge in the DAG going from vertex ‘u’ to vertex ‘v’, then ‘u’ comes before ‘v’ in the ordering. |
It is important to note that-
- Topological Sorting is possible if and only if the graph is a Directed Acyclic Graph.
- There may exist multiple different topological orderings for a given directed acyclic graph.
Topological Sort Example-
Consider the following directed acyclic graph-
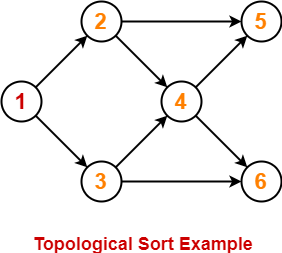
For this graph, following 4 different topological orderings are possible-
- 1 2 3 4 5 6
- 1 2 3 4 6 5
- 1 3 2 4 5 6
- 1 3 2 4 6 5
Applications of Topological Sort-
Few important applications of topological sort are-
- Scheduling jobs from the given dependencies among jobs
- Instruction Scheduling
- Determining the order of compilation tasks to perform in makefiles
- Data Serialization
PRACTICE PROBLEMS BASED ON TOPOLOGICAL SORT-
Problem-01:
Find the number of different topological orderings possible for the given graph-
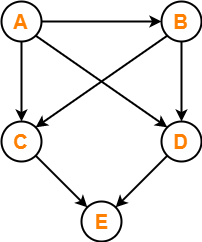
Solution-
The topological orderings of the above graph are found in the following steps-
Step-01:
Write in-degree of each vertex-
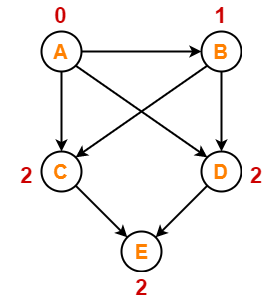
Step-02:
- Vertex-A has the least in-degree.
- So, remove vertex-A and its associated edges.
- Now, update the in-degree of other vertices.
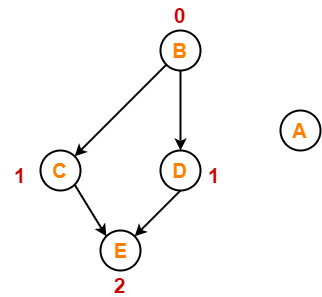
Step-03:
- Vertex-B has the least in-degree.
- So, remove vertex-B and its associated edges.
- Now, update the in-degree of other vertices.
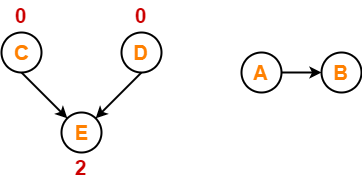
Step-04:
There are two vertices with the least in-degree. So, following 2 cases are possible-
In case-01,
- Remove vertex-C and its associated edges.
- Then, update the in-degree of other vertices.
In case-02,
- Remove vertex-D and its associated edges.
- Then, update the in-degree of other vertices.
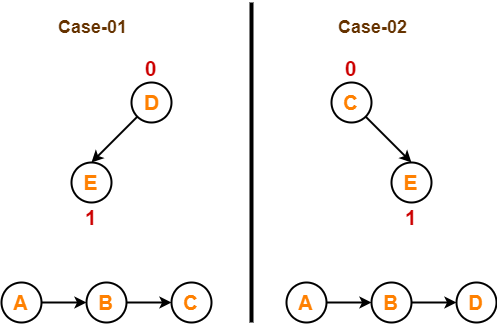
Step-05:
Now, the above two cases are continued separately in the similar manner.
In case-01,
- Remove vertex-D since it has the least in-degree.
- Then, remove the remaining vertex-E.
In case-02,
- Remove vertex-C since it has the least in-degree.
- Then, remove the remaining vertex-E.

Conclusion-
For the given graph, following 2 different topological orderings are possible-
- A B C D E
- A B D C E
Problem-02:
Find the number of different topological orderings possible for the given graph-
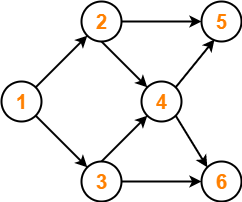
Solution-
The topological orderings of the above graph are found in the following steps-
Step-01:
Write in-degree of each vertex-
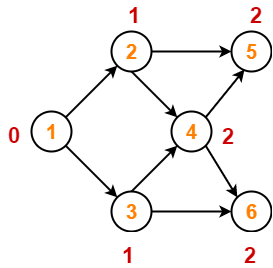
Step-02:
- Vertex-1 has the least in-degree.
- So, remove vertex-1 and its associated edges.
- Now, update the in-degree of other vertices.
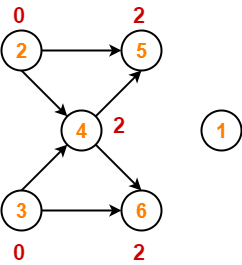
Step-03:
There are two vertices with the least in-degree. So, following 2 cases are possible-
In case-01,
- Remove vertex-2 and its associated edges.
- Then, update the in-degree of other vertices.
In case-02,
- Remove vertex-3 and its associated edges.
- Then, update the in-degree of other vertices.
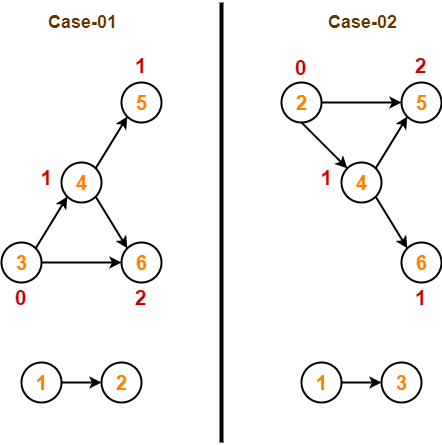
Step-04:
Now, the above two cases are continued separately in the similar manner.
In case-01,
- Remove vertex-3 since it has the least in-degree.
- Then, update the in-degree of other vertices.
In case-02,
- Remove vertex-2 since it has the least in-degree.
- Then, update the in-degree of other vertices.
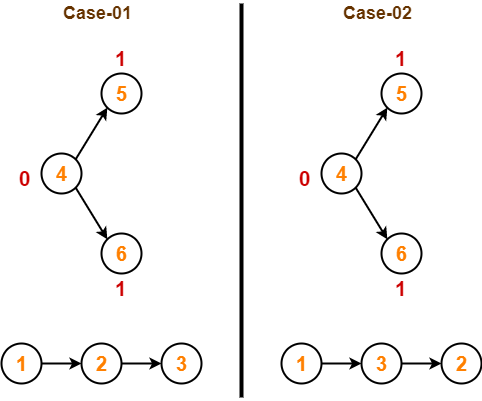
Step-05:
In case-01,
- Remove vertex-4 since it has the least in-degree.
- Then, update the in-degree of other vertices.
In case-02,
- Remove vertex-4 since it has the least in-degree.
- Then, update the in-degree of other vertices.
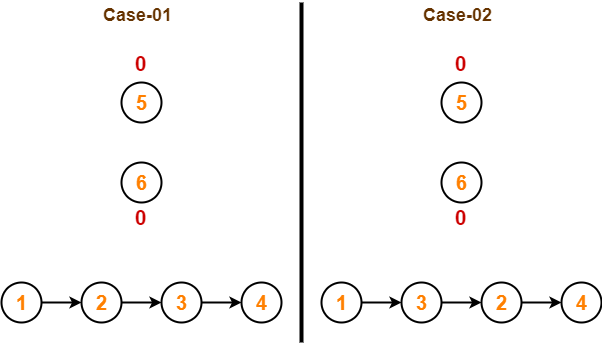
Step-06:
In case-01,
- There are 2 vertices with the least in-degree.
- So, 2 cases are possible.
- Any of the two vertices may be taken first.
Same is with case-02.
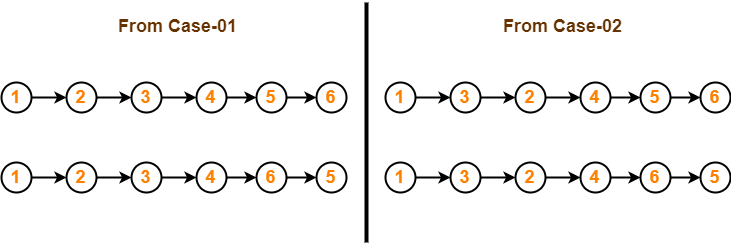
Conclusion-
For the given graph, following 4 different topological orderings are possible-
- 1 2 3 4 5 6
- 1 2 3 4 6 5
- 1 3 2 4 5 6
- 1 3 2 4 6 5
Problem-03:
Consider the directed graph given below. Which of the following statements is true?
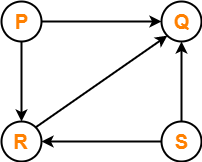
- The graph does not have any topological ordering.
- Both PQRS and SRPQ are topological orderings.
- Both PSRQ and SPRQ are topological orderings.
- PSRQ is the only topological ordering.
Solution-
- The given graph is a directed acyclic graph.
- So, topological orderings exist.
- P and S must appear before R and Q in topological orderings as per the definition of topological sort.
Thus, Correct option is (C).
Problem-04:
Consider the following directed graph-
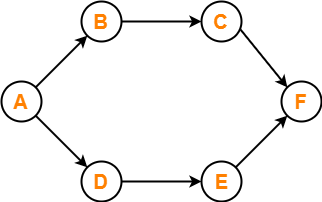
The number of different topological orderings of the vertices of the graph is ________ ?
Solution-
Number of different topological orderings possible = 6.
Thus, Correct answer is 6.
(The solution is explained in detail in the linked video lecture.)
To gain better understanding about Topological Sort,
To practice previous years GATE problems on Topological Sort,
Next Article- Shortest Path Problems
Other Popular Sorting Algorithms-
- Selection Sort | Examples
- Bubble Sort | Examples
- Insertion Sort | Examples
- Merge Sort | Examples
- Quick Sort | Examples
Get more notes and other study material of Design and Analysis of Algorithms.
Watch video lectures by visiting our YouTube channel LearnVidFun.