July, 2018 | Gate Vidyalay

Month: July 2018

Binary Tree | Types of Binary Trees

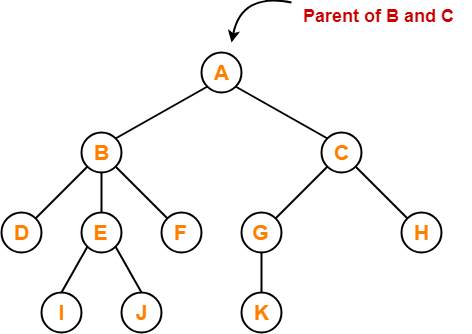
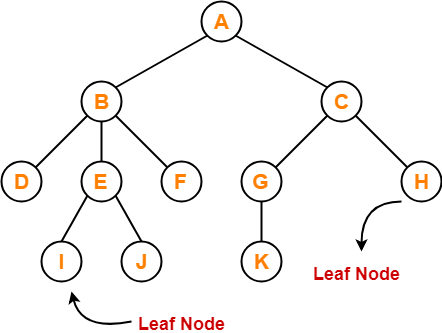
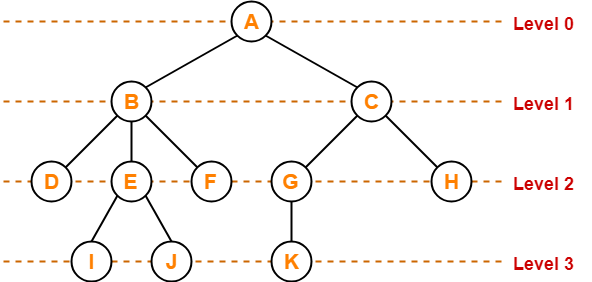
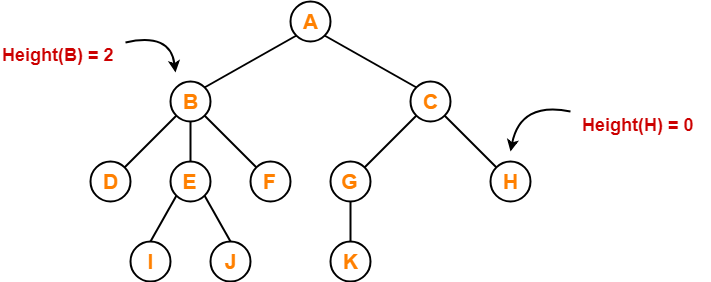
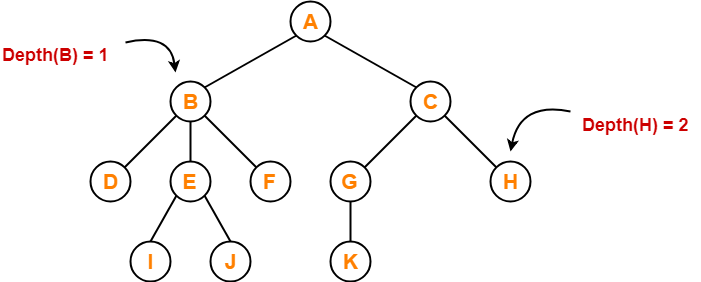
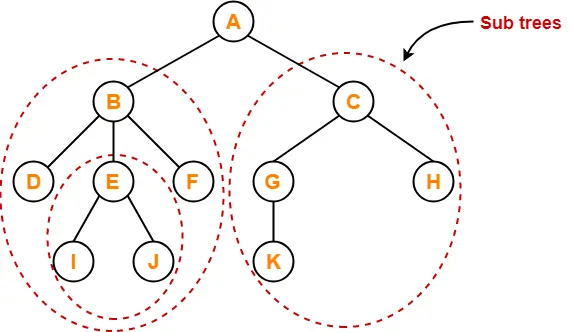
Tree Data Structure-

Before you go through this article, make sure that you have gone through the previous article on Tree Data Structure.

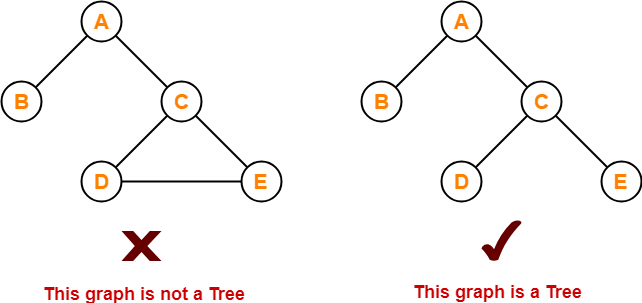
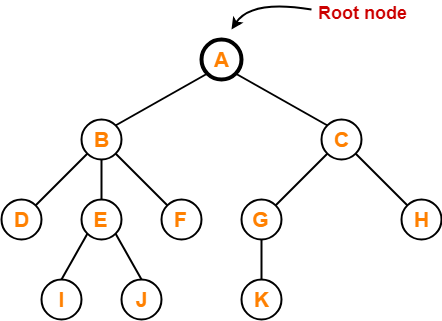
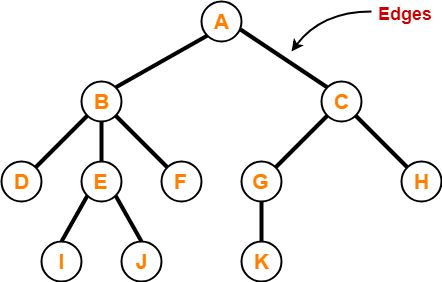
We have discussed-

Tree is a non-linear data structure.
In a tree data structure, a node can have any number of child nodes.

In this article, we will discuss about Binary Trees.

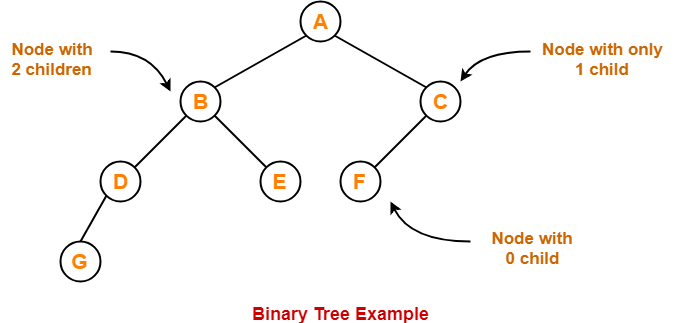
Binary Tree-

Binary tree is a special tree data structure in which each node can have at most 2 children.

Thus, in a binary tree,

Each node has either 0 child or 1 child or 2 children.

Example-

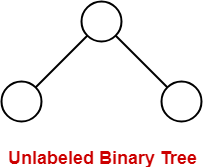
Unlabeled Binary Tree-

A binary tree is unlabeled if its nodes are not assigned any label.

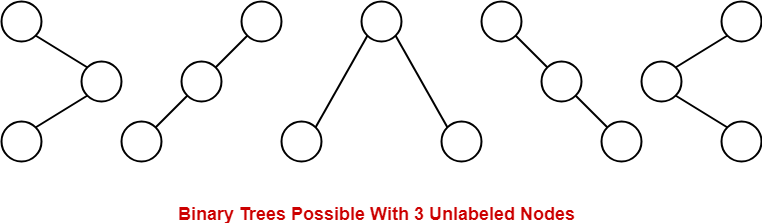
Example-

Consider we want to draw all the binary trees possible with 3 unlabeled nodes.

Using the above formula, we have-

Number of binary trees possible with 3 unlabeled nodes

= ^{2 x 3}C₃ / (3 + 1)

= ⁶C₃ / 4

= 5

Thus,

With 3 unlabeled nodes, 5 unlabeled binary trees are possible.
These unlabeled binary trees are as follows-

Labeled Binary Tree-

A binary tree is labeled if all its nodes are assigned a label.

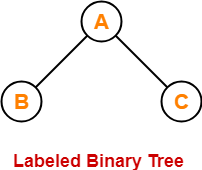
Example-

Consider we want to draw all the binary trees possible with 3 labeled nodes.

Using the above formula, we have-

Number of binary trees possible with 3 labeled nodes

= { ^{2 x 3}C₃ / (3 + 1) } x 3!

= { ⁶C₃ / 4 } x 6

= 5 x 6

= 30

Thus,

With 3 labeled nodes, 30 labeled binary trees are possible.
Each unlabeled structure gives rise to 3! = 6 different labeled structures.

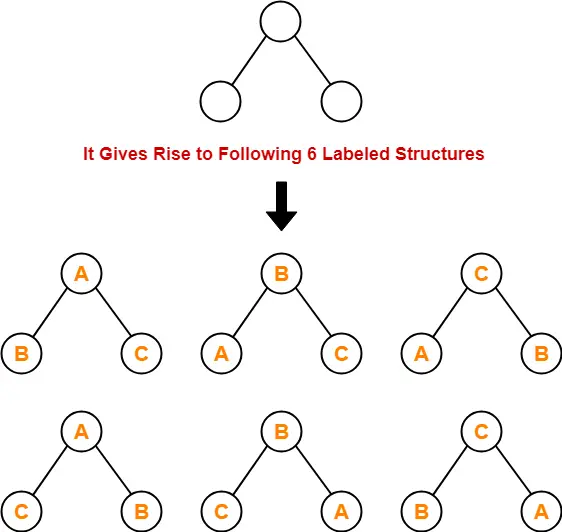
Similarly,

Every other unlabeled structure gives rise to 6 different labeled structures.
Thus, in total 30 different labeled binary trees are possible.

Types of Binary Trees-

Binary trees can be of the following types-

Rooted Binary Tree
Full / Strictly Binary Tree
Complete / Perfect Binary Tree
Almost Complete Binary Tree
Skewed Binary Tree

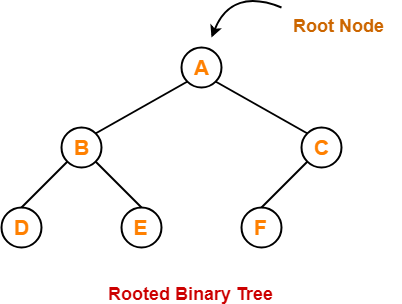
1. Rooted Binary Tree-

A rooted binary tree is a binary tree that satisfies the following 2 properties-

It has a root node.
Each node has at most 2 children.

Example-

2. Full / Strictly Binary Tree-

A binary tree in which every node has either 0 or 2 children is called as a Full binary tree.
Full binary tree is also called as Strictly binary tree.

Example-

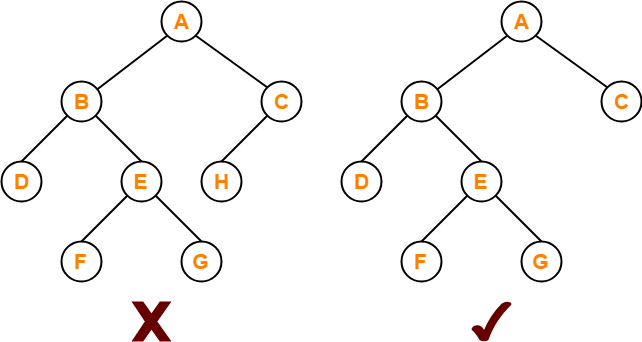
Here,

First binary tree is not a full binary tree.
This is because node C has only 1 child.

3. Complete / Perfect Binary Tree-

A complete binary tree is a binary tree that satisfies the following 2 properties-

Every internal node has exactly 2 children.
All the leaf nodes are at the same level.

Complete binary tree is also called as Perfect binary tree.

Example-

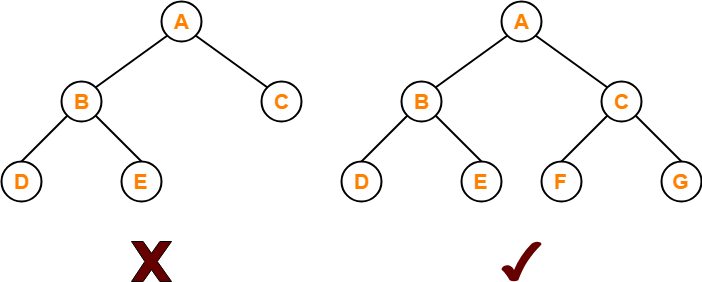
Here,

First binary tree is not a complete binary tree.
This is because all the leaf nodes are not at the same level.

4. Almost Complete Binary Tree-

An almost complete binary tree is a binary tree that satisfies the following 2 properties-

All the levels are completely filled except possibly the last level.
The last level must be strictly filled from left to right.

Example-

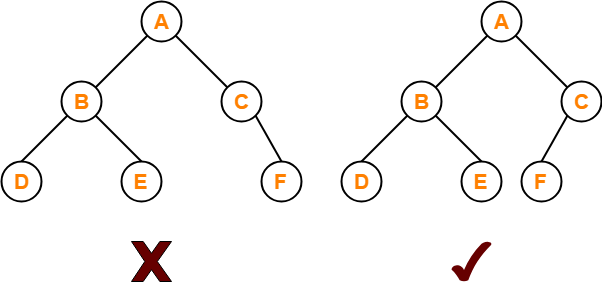
Here,

First binary tree is not an almost complete binary tree.
This is because the last level is not filled from left to right.

5. Skewed Binary Tree-

A skewed binary tree is a binary tree that satisfies the following 2 properties-

All the nodes except one node has one and only one child.
The remaining node has no child.

A skewed binary tree is a binary tree of n nodes such that its depth is (n-1).

Example-

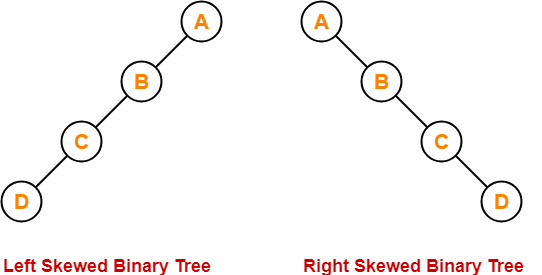
To gain better understanding about Binary Tree and its types-

Watch this Video Lecture

Also Read- Binary Tree Traversal

Download Handwritten Notes Here-

Next Article- Binary Tree Properties

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Tree Data Structure | Tree Terminology

Data Structures

Tree Data Structure-

Tree data structure may be defined as-

Tree is a non-linear data structure which organizes data in a hierarchical structure and this is a recursive definition.

A tree is a connected graph without any circuits.

If in a graph, there is one and only one path between every pair of vertices, then graph is called as a tree.

Example-

Properties-

The important properties of tree data structure are-

There is one and only one path between every pair of vertices in a tree.
A tree with n vertices has exactly (n-1) edges.
A graph is a tree if and only if it is minimally connected.
Any connected graph with n vertices and (n-1) edges is a tree.

To gain better understanding about Tree Data Structure,

Watch this Video Lecture

Tree Terminology-

The important terms related to tree data structure are-

1. Root-

The first node from where the tree originates is called as a root node.
In any tree, there must be only one root node.
We can never have multiple root nodes in a tree data structure.

Example-

Here, node A is the only root node.

2. Edge-

The connecting link between any two nodes is called as an edge.
In a tree with n number of nodes, there are exactly (n-1) number of edges.

Example-

3. Parent-

The node which has a branch from it to any other node is called as a parent node.
In other words, the node which has one or more children is called as a parent node.
In a tree, a parent node can have any number of child nodes.

Example-

Here,

Node A is the parent of nodes B and C
Node B is the parent of nodes D, E and F
Node C is the parent of nodes G and H
Node E is the parent of nodes I and J
Node G is the parent of node K

4. Child-

The node which is a descendant of some node is called as a child node.
All the nodes except root node are child nodes.

Example-

Here,

Nodes B and C are the children of node A
Nodes D, E and F are the children of node B
Nodes G and H are the children of node C
Nodes I and J are the children of node E
Node K is the child of node G

5. Siblings-

Nodes which belong to the same parent are called as siblings.
In other words, nodes with the same parent are sibling nodes.

Example-

Here,

Nodes B and C are siblings
Nodes D, E and F are siblings
Nodes G and H are siblings
Nodes I and J are siblings

6. Degree-

Degree of a node is the total number of children of that node.
Degree of a tree is the highest degree of a node among all the nodes in the tree.

Example-

Here,

Degree of node A = 2
Degree of node B = 3
Degree of node C = 2
Degree of node D = 0
Degree of node E = 2
Degree of node F = 0
Degree of node G = 1
Degree of node H = 0
Degree of node I = 0
Degree of node J = 0
Degree of node K = 0

7. Internal Node-

The node which has at least one child is called as an internal node.
Internal nodes are also called as non-terminal nodes.
Every non-leaf node is an internal node.

Example-

Here, nodes A, B, C, E and G are internal nodes.

8. Leaf Node-

The node which does not have any child is called as a leaf node.
Leaf nodes are also called as external nodes or terminal nodes.

Example-

Here, nodes D, I, J, F, K and H are leaf nodes.

9. Level-

In a tree, each step from top to bottom is called as level of a tree.
The level count starts with 0 and increments by 1 at each level or step.

Example-

10. Height-

Total number of edges that lies on the longest path from any leaf node to a particular node is called as height of that node.
Height of a tree is the height of root node.
Height of all leaf nodes = 0

Example-

Here,

Height of node A = 3
Height of node B = 2
Height of node C = 2
Height of node D = 0
Height of node E = 1
Height of node F = 0
Height of node G = 1
Height of node H = 0
Height of node I = 0
Height of node J = 0
Height of node K = 0

11. Depth-

Total number of edges from root node to a particular node is called as depth of that node.
Depth of a tree is the total number of edges from root node to a leaf node in the longest path.
Depth of the root node = 0
The terms “level” and “depth” are used interchangeably.

Example-

Here,

Depth of node A = 0
Depth of node B = 1
Depth of node C = 1
Depth of node D = 2
Depth of node E = 2
Depth of node F = 2
Depth of node G = 2
Depth of node H = 2
Depth of node I = 3
Depth of node J = 3
Depth of node K = 3

12. Subtree-

In a tree, each child from a node forms a subtree recursively.
Every child node forms a subtree on its parent node.

Example-

13. Forest-

A forest is a set of disjoint trees.

Example-

To gain better understanding about Tree Terminology,

Watch this Video Lecture

Download Handwritten Notes Here-

Next Article- Binary Tree | Types of Binary Trees

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.

GATE Exam | GATE 2019 | Important Notifications

GATE

About GATE-

The Graduate Aptitude Test in Engineering popularly called as GATE is an All-India examination.
It is administered by the GATE Committee consisting of Faculty members from IISc, Bangalore and other seven IIT’s and the exam is conducted in eight zones across the country.

The score or rank obtained in GATE exam is mainly used for the following purposes-

Used for admissions to Post Graduate Programmes (ME, M.Tech, MS, Direct Ph.D.) in institutes like IITs and IISc etc with financial assistance offered by Ministry of Human Resource and Development (MHRD).
Used by PSUs for recruiting candidates for various prestigious jobs with attractive remuneration.

Conducting Authority for GATE 2019-

IIT Madras is the conducting authority of GATE 2019 examination.

Important Dates for GATE 2019-

GATE Online Application Processing System (GOAPS) Website Opens	Saturday	01^st September 2018
Closing Date for Submission of Application (Online through website)	Friday	21^st September 2018
Extended Closing Date for Submission of Application (Online through website)	Monday	01^st October 2018
Last Date for Requesting Change of Examination City (An additional fee applicable)	Friday	16^th November 2018
Admit Card will be available on the portal for printing	Friday	04^th January 2018
GATE 2019 Examination Forenoon: 9:00 AM to 12:00 Noon (Tentative) Afternoon: 2:00 PM to 5:00 PM (Tentative)	Saturday Sunday Saturday Sunday	02^nd February 2019 03^rd February 2019 09^th February 2019 10^th February 2019
Release of GATE 2019 Response Sheets	–	2^nd Week of February 2019
Release of GATE 2019 Answer Key	–	3^rd Week of February 2019
Announcement of the Results on the portal	Saturday	16^th March 2019

Eligibility Criteria for GATE 2019-

There are certain criteria that a candidate must fulfill to appear for GATE exam. Candidates must fulfill the following criteria-

There is no age limit for GATE aspirants.
Indian and Foreign National candidates are eligible to apply.
It is compulsory for all the candidates to have completed or be in their final year of B.E./B.Tech or Post-Graduate (M.Sc) degree in the relevant subject.
There is no minimum pass percentage in the qualifying degree.

Application Fee for GATE 2019-

The application fee is different for different candidates based on their category and location of examination center-

For examination centers in India-

	On or Before 21^st September 2018	During the extended period
Female Candidates	Rs. 750/-	Rs. 1250/-
SC / ST / Person with Disability Category Students	Rs. 750/-	Rs. 1250/-
All other candidates	Rs. 1500/-	Rs. 2000/-

For examination centers Outside India (All Candidates)-

	On or Before 21^st September 2018	During the extended period
Addis Ababa, Colombo, Dhaka and Kathmandu	US$ 50	US$ 70
Dubai and Singapore	US$ 100	US$ 120

Note-

It is important to note that the above mentioned application fee DOES NOT INCLUDE processing fees, service charges or any other charges that the bank may impose.

Exam Pattern for GATE 2019-

Online Computer Based Test
3 hours to complete the exam
MCQ and Numerical Type Questions
65 Questions, 100 marks
One-third negative mark in MCQ for wrong answers
No negative marking for Numerical Type Questions

Division of Questions and Marks-

As mentioned above, there will be total 65 question carrying 100 marks. The paper will be divided into 2 sections- General Aptitude and Technical.

General Aptitude Section will consist of 10 Questions carrying 15 marks.
Technical Section will consist of 55 Questions carrying 85 marks. Out of these, Engineering Mathematics will comprise of 15 marks.

Section	Question No.	No. of Questions	Marks per Question	Total Marks
General Aptitude	1 to 5	5	1	5
General Aptitude	6 to 10	5	2	10
Technical + Engineering Mathematics	1 to 25	25	1	25
Technical + Engineering Mathematics	26 to 55	30	2	60
		Total Questions: 65		Total Marks: 100

Syllabus for GATE 2019-

Candidates from CS/IT branch may download the GATE 2019 syllabus from here-

GATE 2019 syllabus (Technical) for Computer Science Students

GATE 2019 syllabus (General Aptitude) common for all branches

Candidates from other branches may download the syllabus from here.

For more details, visit GATE 2019 Official Website.

Difference Between Prim’s and Kruskal’s Algorithm

Design & Analysis of Algorithms

Prim’s and Kruskal’s Algorithms-

Before you go through this article, make sure that you have gone through the previous articles on Prim’s Algorithm & Kruskal’s Algorithm.

We have discussed-

Prim’s and Kruskal’s Algorithm are the famous greedy algorithms.
They are used for finding the Minimum Spanning Tree (MST) of a given graph.
To apply these algorithms, the given graph must be weighted, connected and undirected.

Some important concepts based on them are-

Concept-01:

If all the edge weights are distinct, then both the algorithms are guaranteed to find the same MST.

Example-

Consider the following example-

Here, both the algorithms on the above given graph produces the same MST as shown.

Concept-02:

If all the edge weights are not distinct, then both the algorithms may not always produce the same MST.
However, cost of both the MST_s would always be same in both the cases.

Example-

Consider the following example-

Here, both the algorithms on the above given graph produces different MST_s as shown but the cost is same in both the cases.

Concept-03:

Kruskal’s Algorithm is preferred when-

The graph is sparse.
There are less number of edges in the graph like E = O(V)
The edges are already sorted or can be sorted in linear time.

Prim’s Algorithm is preferred when-

The graph is dense.
There are large number of edges in the graph like E = O(V²).

Concept-04:

Difference between Prim’s Algorithm and Kruskal’s Algorithm-

Prim’s Algorithm	Kruskal’s Algorithm
The tree that we are making or growing always remains connected.	The tree that we are making or growing usually remains disconnected.
Prim’s Algorithm grows a solution from a random vertex by adding the next cheapest vertex to the existing tree.	Kruskal’s Algorithm grows a solution from the cheapest edge by adding the next cheapest edge to the existing tree / forest.
Prim’s Algorithm is faster for dense graphs.	Kruskal’s Algorithm is faster for sparse graphs.

To gain better understanding about Difference between Prim’s and Kruskal’s Algorithm,

Watch this Video Lecture

Next Article- Linear Search

Get more notes and other study material of Design and Analysis of Algorithms.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Kruskal’s Algorithm | Kruskal’s Algorithm Example | Problems

Design & Analysis of Algorithms

Kruskal’s Algorithm-

Kruskal’s Algorithm is a famous greedy algorithm.
It is used for finding the Minimum Spanning Tree (MST) of a given graph.
To apply Kruskal’s algorithm, the given graph must be weighted, connected and undirected.

Kruskal’s Algorithm Implementation-

The implementation of Kruskal’s Algorithm is explained in the following steps-

Step-01:

Sort all the edges from low weight to high weight.

Step-02:

Take the edge with the lowest weight and use it to connect the vertices of graph.
If adding an edge creates a cycle, then reject that edge and go for the next least weight edge.