Graphs-
- A graph is a collection of vertices connected to each other through a set of edges.
- The study of graphs is known as Graph Theory.
Formal DefinitionFormally, A graph is defined as an ordered pair of a set of vertices and a set of edges. G = (V, E) Here, V is the set of vertices and E is the set of edges connecting the vertices. |
Example-
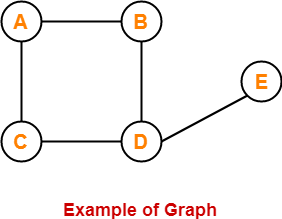
In this graph,
V = { A , B , C , D , E }
E = { AB , AC , BD , CD , DE }
Types of Graphs-
Various important types of graphs in graph theory are-

- Null Graph
- Trivial Graph
- Non-directed Graph
- Directed Graph
- Connected Graph
- Disconnected Graph
- Regular Graph
- Complete Graph
- Cycle Graph
- Cyclic Graph
- Acyclic Graph
- Finite Graph
- Infinite Graph
- Bipartite Graph
- Planar Graph
- Simple Graph
- Multi Graph
- Pseudo Graph
- Euler Graph
- Hamiltonian Graph
1. Null Graph-
- A graph whose edge set is empty is called as a null graph.
- In other words, a null graph does not contain any edges in it.
Example-
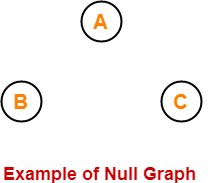
Here,
- This graph consists only of the vertices and there are no edges in it.
- Since the edge set is empty, therefore it is a null graph.
2. Trivial Graph-
- A graph having only one vertex in it is called as a trivial graph.
- It is the smallest possible graph.
Example-

Here,
- This graph consists of only one vertex and there are no edges in it.
- Since only one vertex is present, therefore it is a trivial graph.
3. Non-Directed Graph-
- A graph in which all the edges are undirected is called as a non-directed graph.
- In other words, edges of an undirected graph do not contain any direction.
Example-
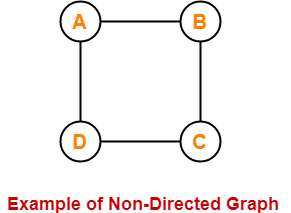
Here,
- This graph consists of four vertices and four undirected edges.
- Since all the edges are undirected, therefore it is a non-directed graph.
4. Directed Graph-
- A graph in which all the edges are directed is called as a directed graph.
- In other words, all the edges of a directed graph contain some direction.
- Directed graphs are also called as digraphs.
Example-
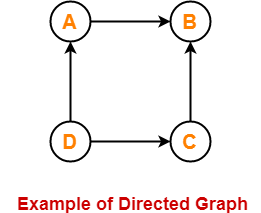
Here,
- This graph consists of four vertices and four directed edges.
- Since all the edges are directed, therefore it is a directed graph.
5. Connected Graph-
- A graph in which we can visit from any one vertex to any other vertex is called as a connected graph.
- In connected graph, at least one path exists between every pair of vertices.
Example-
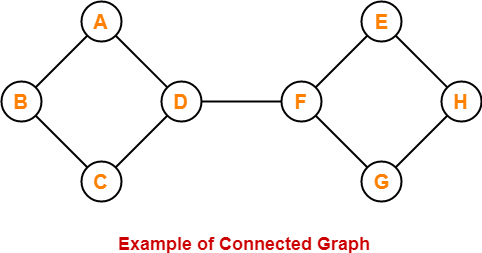
Here,
- In this graph, we can visit from any one vertex to any other vertex.
- There exists at least one path between every pair of vertices.
- Therefore, it is a connected graph.
6. Disconnected Graph-
- A graph in which there does not exist any path between at least one pair of vertices is called as a disconnected graph.
Example-
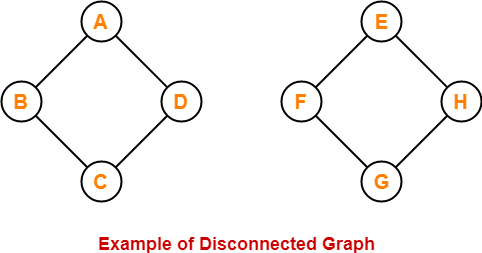
Here,
- This graph consists of two independent components which are disconnected.
- It is not possible to visit from the vertices of one component to the vertices of other component.
- Therefore, it is a disconnected graph.
7. Regular Graph-
- A graph in which degree of all the vertices is same is called as a regular graph.
- If all the vertices in a graph are of degree ‘k’, then it is called as a “k-regular graph“.
Examples-
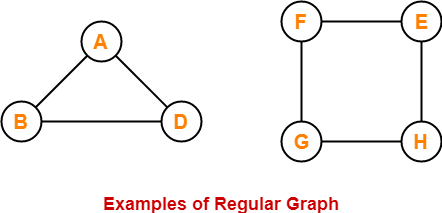
In these graphs,
- All the vertices have degree-2.
- Therefore, they are 2-Regular graphs.
8. Complete Graph-
- A graph in which exactly one edge is present between every pair of vertices is called as a complete graph.
- A complete graph of ‘n’ vertices contains exactly nC2 edges.
- A complete graph of ‘n’ vertices is represented as Kn.
Examples-
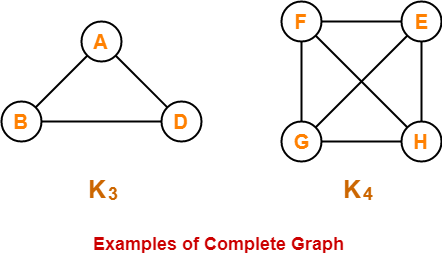
In these graphs,
- Each vertex is connected with all the remaining vertices through exactly one edge.
- Therefore, they are complete graphs.
9. Cycle Graph-
- A simple graph of ‘n’ vertices (n>=3) and n edges forming a cycle of length ‘n’ is called as a cycle graph.
- In a cycle graph, all the vertices are of degree 2.
Examples-
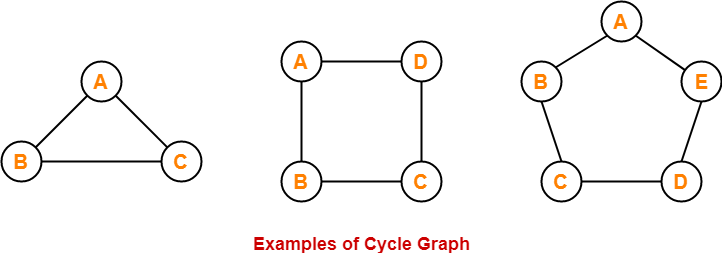
In these graphs,
- Each vertex is having degree 2.
- Therefore, they are cycle graphs.
10. Cyclic Graph-
- A graph containing at least one cycle in it is called as a cyclic graph.
Example-
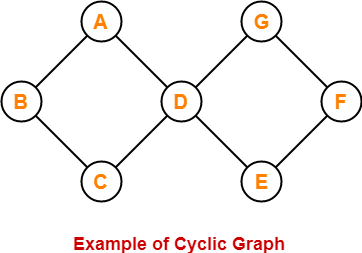
Here,
- This graph contains two cycles in it.
- Therefore, it is a cyclic graph.
11. Acyclic Graph-
- A graph not containing any cycle in it is called as an acyclic graph.
Example-
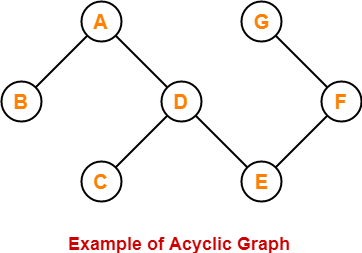
Here,
- This graph do not contain any cycle in it.
- Therefore, it is an acyclic graph.
12. Finite Graph-
- A graph consisting of finite number of vertices and edges is called as a finite graph.
Example-
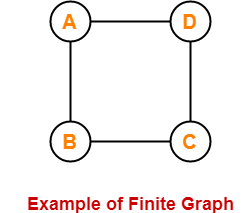
Here,
- This graph consists of finite number of vertices and edges.
- Therefore, it is a finite graph.
13. Infinite Graph-
- A graph consisting of infinite number of vertices and edges is called as an infinite graph.
Example-

Here,
- This graph consists of infinite number of vertices and edges.
- Therefore, it is an infinite graph.
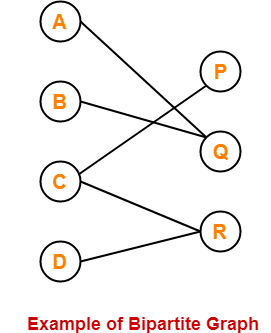
14. Bipartite Graph-
A bipartite graph is a graph where-
- Vertices can be divided into two sets X and Y.
- The vertices of set X only join with the vertices of set Y.
- None of the vertices belonging to the same set join each other.
Example-
Read More- Bipartite Graphs
15. Planar Graph-
- A planar graph is a graph that we can draw in a plane such that no two edges of it cross each other.
Example-
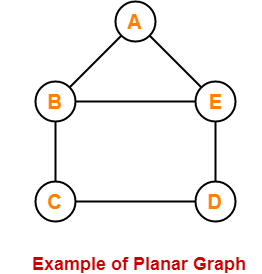
Here,
- This graph can be drawn in a plane without crossing any edges.
- Therefore, it is a planar graph.
Read More- Planar Graphs
16. Simple Graph-
- A graph having no self loops and no parallel edges in it is called as a simple graph.
Example-

Here,
- This graph consists of three vertices and three edges.
- There are neither self loops nor parallel edges.
- Therefore, it is a simple graph.
17. Multi Graph-
- A graph having no self loops but having parallel edge(s) in it is called as a multi graph.
Example-
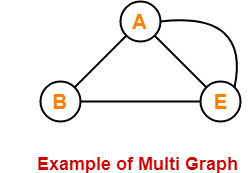
Here,
- This graph consists of three vertices and four edges out of which one edge is a parallel edge.
- There are no self loops but a parallel edge is present.
- Therefore, it is a multi graph.
18. Pseudo Graph-
- A graph having no parallel edges but having self loop(s) in it is called as a pseudo graph.
Example-
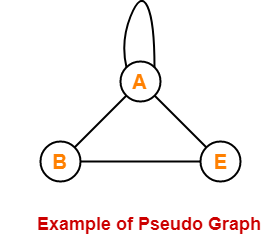
Here,
- This graph consists of three vertices and four edges out of which one edge is a self loop.
- There are no parallel edges but a self loop is present.
- Therefore, it is a pseudo graph.
19. Euler Graph-
- Euler Graph is a connected graph in which all the vertices are even degree.
Example-
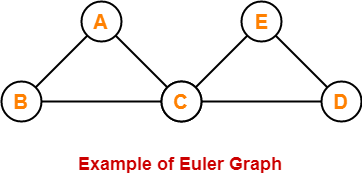
Here,
- This graph is a connected graph.
- The degree of all the vertices is even.
- Therefore, it is an Euler graph.
Read More- Euler Graphs
20. Hamiltonian Graph-
- If there exists a closed walk in the connected graph that visits every vertex of the graph exactly once (except starting vertex) without repeating the edges, then such a graph is called as a Hamiltonian graph.
Example-
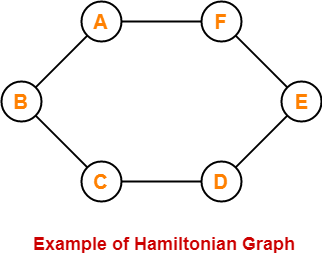
Here,
- This graph contains a closed walk ABCDEFG that visits all the vertices (except starting vertex) exactly once.
- All the vertices are visited without repeating the edges.
- Therefore, it is a Hamiltonian Graph.
Read More- Hamiltonian Graphs
Important Points-
- Edge set of a graph can be empty but vertex set of a graph can not be empty.
- Every polygon is a 2-Regular Graph.
- Every complete graph of ‘n’ vertices is a (n-1)-regular graph.
- Every regular graph need not be a complete graph.
Remember-
The following table is useful to remember different types of graphs-
| Self-Loop(s) | Parallel Edge(s) | |
| Graph | Yes | Yes |
| Simple Graph | No | No |
| Multi Graph | No | Yes |
| Pseudo Graph | Yes | No |
Applications of Graph Theory-
Graph theory has its applications in diverse fields of engineering-
1. Electrical Engineering-
- The concepts of graph theory are used extensively in designing circuit connections.
- The types or organization of connections are named as topologies.
- Some examples for topologies are star, bridge, series and parallel topologies.
2. Computer Science-
Graph theory is used for the study of algorithms such as-
3. Computer Network-
The relationships among interconnected computers in the network follows the principles of graph theory.
4. Science-
Following structures are represented by graphs-
- Molecular structure of a substance
- Chemical structure of a substance
- DNA structure of an organism etc
5. Linguistics-
The parsing tree of a language and grammar of a language uses graphs.
6. Other Applications-
- Routes between the cities are represented using graphs.
- Hierarchical ordered information such as family tree are represented using special types of graphs called trees.
Next Article- Planar Graph
Get more notes and other study material of Graph Theory.
Watch video lectures by visiting our YouTube channel LearnVidFun.