Complement of Graph in Graph Theory | Example | Problems

Complement Of Graph-

 

Complement of a simple graph G is a simple graph G’ having-

• All the vertices of G.
• An edge between two vertices v and w iff there exists no edge between v and w in the original graph G.

 

Complement Of Graph Example-

 

The following example shows a graph G and its complement graph G’-

 

 

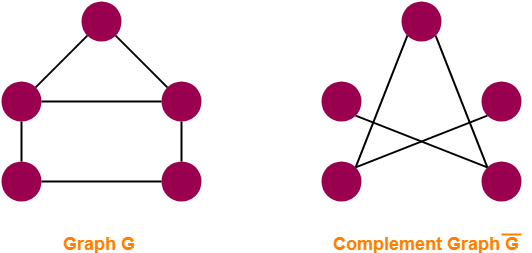
Relationship Between G & G’-

 

The following relationship exists between a graph G and its complement graph G’-

 

1. Number of vertices in G = Number of vertices in G’.

 

|V(G)| = |V(G’)|

 

2. The sum of total number of edges in G and G’ is equal to the total number of edges in a complete graph.

 

|E(G)| + |E(G’)| = C(n,2) = n(n-1) / 2

where n = total number of vertices in the graph

 

Important Terms-

 

It is important to note the following terms-

• Order of graph = Total number of vertices in the graph
• Size of graph = Total number of edges in the graph

 

Also Read- Types of Graphs in Graph Theory

 

PRACTICE PROBLEMS BASED ON COMPLEMENT OF GRAPH IN GRAPH THEORY-

 

Problem-01:

 

A simple graph G has 10 vertices and 21 edges. Find total number of edges in its complement graph G’.

 

Solution-

 

Given-

• Number of edges in graph G, |E(G)| = 21
• Number of vertices in graph G, n = 10

 

We know |E(G)| + |E(G’)| = n(n-1) / 2.

 

Substituting the values, we get-

21 + |E(G’)| = 10 x (10-1) / 2

|E(G’)| = 45 – 21

∴ |E(G’)| = 24

 

Thus, Number of edges in complement graph G’ = 24.

 

Problem-02:

 

A simple graph G has 30 edges and its complement graph G’ has 36 edges. Find number of vertices in G.

 

Solution-

 

Given-

• Number of edges in graph G, |E(G)| = 30
• Number of edges in graph G’, |E(G’)| = 36

 

We know |E(G)| + |E(G’)| = n(n-1) / 2.

 

Substituting the values, we get-

30 + 36 = n(n-1) / 2

n(n-1) = 132

n² – n – 132 = 0

Solving this quadratic equation, we get n = 12.

 

Thus, Number of vertices in graph G = 12.

 

Problem-03:

 

Let G be a simple graph of order n. If the size of G is 56 and the size of G’ is 80. What is n?

 

Solution-

 

Size of a graph = Number of edges in the graph.

 

Given-

• Number of edges in graph G, |E(G)| = 56
• Number of edges in graph G’, |E(G’)| = 80

 

We know |E(G)| + |E(G’)| = n(n-1) / 2.

 

Substituting the values, we get-

56 + 80 = n(n-1) / 2

n(n-1) = 272

n² – n – 272 = 0

Solving this quadratic equation, we get n = 17.

 

Thus, Number of vertices in graph G = 17.

In other words, Order of graph G = 17.

 

To gain better understanding about Complement Of Graph,

Watch this Video Lecture

 

Next Article- Walks in Graph Theory

 

Get more notes and other study material of Graph Theory.

Watch video lectures by visiting our YouTube channel LearnVidFun.