Separate Chaining | Collision Resolution Techniques

Hashing in Data Structure-

 

Before you go through this article, make sure that you have gone through the previous article on Hashing.

 

We have discussed-

• Hashing is a well-known searching technique.
• It minimizes the number of comparisons while performing the search.
• It completes the search with constant time complexity O(1).

 

In this article, we will discuss about Collisions in Hashing.

 

Collision in Hashing-

 

In hashing,

• Hash function is used to compute the hash value for a key.
• Hash value is then used as an index to store the key in the hash table.
• Hash function may return the same hash value for two or more keys.

 

When the hash value of a key maps to an already occupied bucket of the hash table, it is called as a Collision.

 

Collision Resolution Techniques-

 

Collision Resolution Techniques are the techniques used for resolving or handling the collision.

 

Collision resolution techniques are classified as-

 

 

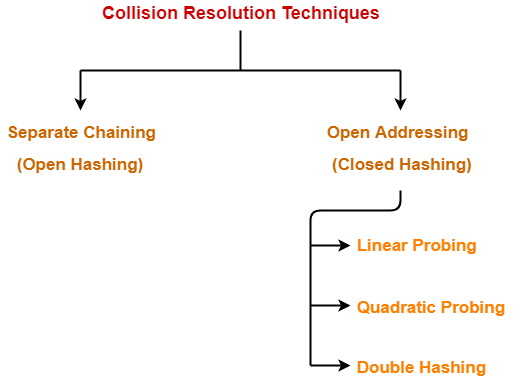
1. Separate Chaining
2. Open Addressing

 

In this article, we will discuss about separate chaining.

 

Separate Chaining-

 

To handle the collision,

• This technique creates a linked list to the slot for which collision occurs.
• The new key is then inserted in the linked list.
• These linked lists to the slots appear like chains.
• That is why, this technique is called as separate chaining.

 

Time Complexity-

 

For Searching-

 

• In worst case, all the keys might map to the same bucket of the hash table.
• In such a case, all the keys will be present in a single linked list.
• Sequential search will have to be performed on the linked list to perform the search.
• So, time taken for searching in worst case is O(n).

 

For Deletion-

 

• In worst case, the key might have to be searched first and then deleted.
• In worst case, time taken for searching is O(n).
• So, time taken for deletion in worst case is O(n).

 

Load Factor (α)-

 

Load factor (α) is defined as-

 

 

If Load factor (α) = constant, then time complexity of Insert, Search, Delete = Θ(1)

 

PRACTICE PROBLEM BASED ON SEPARATE CHAINING-

 

Problem-

 

Using the hash function ‘key mod 7’, insert the following sequence of keys in the hash table-

50, 700, 76, 85, 92, 73 and 101

 

Use separate chaining technique for collision resolution.

 

Solution-

 

The given sequence of keys will be inserted in the hash table as-

 

Step-01:

 

• Draw an empty hash table.
• For the given hash function, the possible range of hash values is [0, 6].
• So, draw an empty hash table consisting of 7 buckets as-

 

 

Step-02:

 

• Insert the given keys in the hash table one by one.
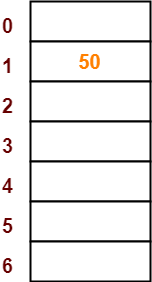
• The first key to be inserted in the hash table = 50.
• Bucket of the hash table to which key 50 maps = 50 mod 7 = 1.
• So, key 50 will be inserted in bucket-1 of the hash table as-

 

 

Step-03:

 

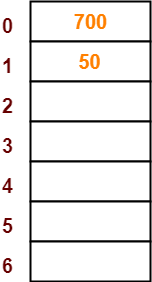
• The next key to be inserted in the hash table = 700.
• Bucket of the hash table to which key 700 maps = 700 mod 7 = 0.
• So, key 700 will be inserted in bucket-0 of the hash table as-

 

 

Step-04:

 

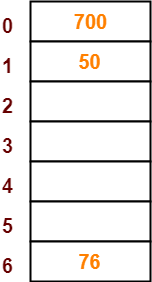
• The next key to be inserted in the hash table = 76.
• Bucket of the hash table to which key 76 maps = 76 mod 7 = 6.
• So, key 76 will be inserted in bucket-6 of the hash table as-

 

 

Step-05:

 

• The next key to be inserted in the hash table = 85.
• Bucket of the hash table to which key 85 maps = 85 mod 7 = 1.
• Since bucket-1 is already occupied, so collision occurs.
• Separate chaining handles the collision by creating a linked list to bucket-1.
• So, key 85 will be inserted in bucket-1 of the hash table as-

 

 

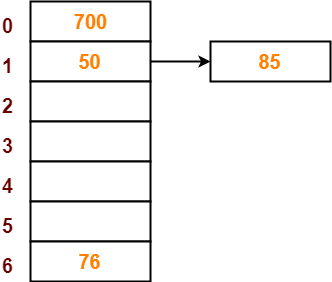
Step-06:

 

• The next key to be inserted in the hash table = 92.
• Bucket of the hash table to which key 92 maps = 92 mod 7 = 1.
• Since bucket-1 is already occupied, so collision occurs.
• Separate chaining handles the collision by creating a linked list to bucket-1.
• So, key 92 will be inserted in bucket-1 of the hash table as-

 

 

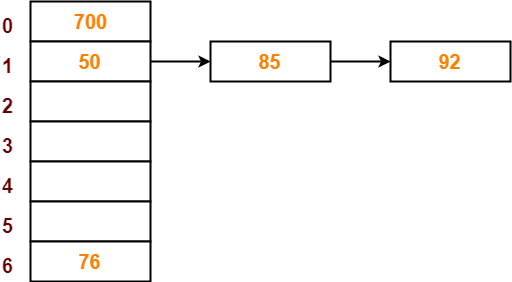
Step-07:

 

• The next key to be inserted in the hash table = 73.
• Bucket of the hash table to which key 73 maps = 73 mod 7 = 3.
• So, key 73 will be inserted in bucket-3 of the hash table as-

 

 

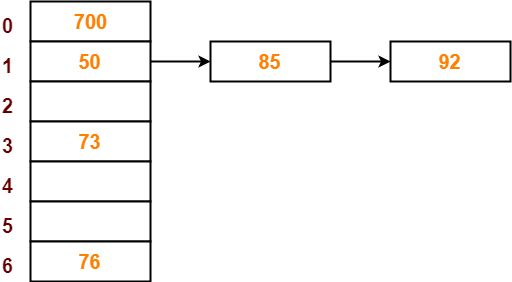
Step-08:

 

• The next key to be inserted in the hash table = 101.
• Bucket of the hash table to which key 101 maps = 101 mod 7 = 3.
• Since bucket-3 is already occupied, so collision occurs.
• Separate chaining handles the collision by creating a linked list to bucket-3.
• So, key 101 will be inserted in bucket-3 of the hash table as-

 

 

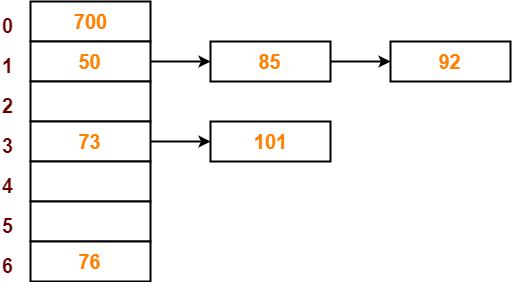
To gain better understanding about Separate Chaining,

Watch this Video Lecture

 

Next Article- Open Addressing

 

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.