Binary Exponential BackOff Algorithm | CSMA CD

CSMA / CD Protocol-

 

Before you go through this article, make sure that you have gone through the previous article on CSMA / CD Protocol.

 

We have discussed-

• CSMA / CD stands for Carrier Sense Multiple Access / Collision Detection.
• It allows the stations to sense the carrier and transmit data if the carrier is free.

 

The following CSMA / CD flowchart shows the CSMA / CD procedure-

 

 

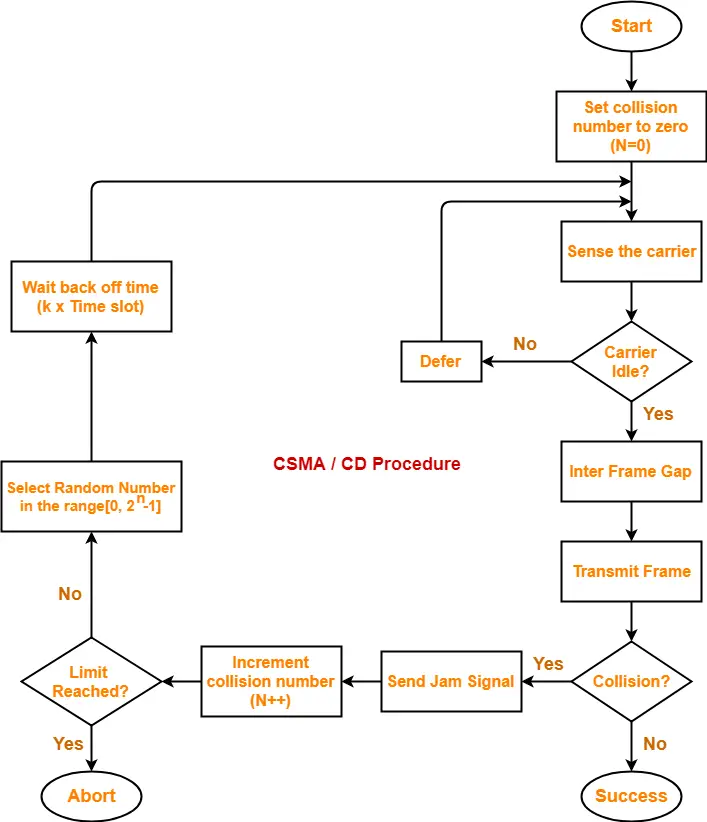
Back Off Time-

 

In CSMA / CD protocol,

• After the occurrence of collision, station waits for some random back off time and then retransmits.
• This waiting time for which the station waits before retransmitting the data is called as back off time.
• Back Off Algorithm is used for calculating the back off time.

 

Back Off Algorithm-

 

After undergoing the collision,

• Transmitting station chooses a random number in the range [0, 2ⁿ-1] if the packet is undergoing collision for the n^th time.
• If station chooses a number k, then-

 

Back off time = k x Time slot

where value of one time slot = 1 RTT

 

Example-

 

Consider the following scenario where stations A and D start transmitting their data simultaneously-

 

 

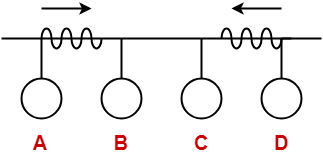
For simplicity,

• We consider the value of time slot = 1 unit.
• Thus, back off time = K units.

 

Scene-01: For 1st Data Packet Of Both Stations-

 

• Both the stations start transmitting their 1^st data packet simultaneously.
• This leads to a collision.
• Clearly, the collision on both the packets is occurring for the 1^st time.
• So, collision number for the 1^st data packet of both the stations = 1.

 

At Station A-

 

After detecting the collision,

• Station A randomly chooses a number in the range [0, 2¹-1] = [0,1].
• If station A chooses the number K_A, then back off time = K_A units.

 

At Station D-

 

After detecting the collision,

• Station D randomly chooses a number in the range [0, 2¹-1] = [0,1].
• If station D chooses the number K_D, then back off time = K_D units.

 

Following 4 cases are possible-

 

KA	KD	Remarks
0	0	In this case, both the stations start retransmitting their data immediately. This case leads to a collision again.
0	1	In this case, station A starts retransmitting its data immediately while station D waits for 1 unit of time. This case leads to A successfully retransmitting its data after the 1st collision.
1	0	In this case, station A waits for 1 unit of time while station D starts retransmitting its data immediately. This case leads to D successfully retransmitting its data after the 1st collision.
1	1	In this case, both the stations wait for 1 unit of time and then starts retransmitting their data simultaneously. This case leads to a collision again.

 

From here,

• Probability of station A to successfully retransmit its data after the 1^st collision = 1 / 4
• Probability of station D to successfully retransmit its data after the 1^st collision = 1 / 4
• Probability of occurrence of collision again after the 1^st collision = 2 / 4 = 1 / 2

 

Now,

• Consider case-02 occurs.
• This causes station A to successfully retransmit its 1^st packet after the 1^st collision.

 

Scene-02: For 2nd Data Packet Of Station A And 1st Data Packet Of Station D-

 

Consider after some time,

• Station A starts transmitting its 2^nd data packet and station D starts retransmitting its 1^st data packet simultaneously.
• This leads to a collision.

 

At Station A-

 

• The 2^nd data packet of station A undergoes collision for the 1^st time.
• So, collision number for the 2^nd data packet of station A = 1.
• Now, station A randomly chooses a number in the range [0, 2¹-1] = [0,1].
• If station A chooses the number K_A, then back off time = K_A units.

 

At Station D-

 

• The 1^st data packet of station D undergoes collision for the 2^nd time.
• So, collision number for the 1^st data packet of station D = 2.
• Now, station D randomly chooses a number in the range [0, 2²-1] = [0,3].
• If station D chooses the number K_D, then back off time = K_D units.

 

Following 8 cases are possible-

 

KA	KD	Remarks
0	0	In this case, both the stations start retransmitting their data immediately. This case leads to a collision again.
0	1	In this case, station A starts retransmitting its data immediately while station D waits for 1 unit of time. This case leads to A successfully retransmitting its data after the 2nd collision.
0	2	In this case, station A starts retransmitting its data immediately while station D waits for 2 unit of time. This case leads to A successfully retransmitting its data after the 2nd collision.
0	3	In this case, station A starts retransmitting its data immediately while station D waits for 3 unit of time. This case leads to A successfully retransmitting its data after the 2nd collision.
1	0	In this case, station A waits for 1 unit of time while station D starts retransmitting its data immediately. This case leads to D successfully retransmitting its data after the 2nd collision.
1	1	In this case, both the stations wait for 1 unit of time and then starts retransmitting their data simultaneously. This case leads to a collision again.
1	2	In this case, station A waits for 1 unit of time while station D waits for 2 unit of time. This case leads to A successfully retransmitting its data after the 2nd collision.
1	3	In this case, station A waits for 1 unit of time while station D waits for 3 unit of time. This case leads to A successfully retransmitting its data after the 2nd collision.

 

From here,

• Probability of station A to successfully retransmit its data after the 2^nd collision = 5 / 8
• Probability of station D to successfully retransmit its data after the 2^nd collision = 1 / 8
• Probability of occurrence of collision again after the 2^nd collision = 2 / 8 = 1 / 4

 

Now,

• Consider case-03 occurs.
• This causes station A to successfully retransmit its 2^nd packet after the 2^nd collision.

 

Scene-03: For 3rd Data Packet Of Station A And 1st Data Packet Of Station D-

 

Consider after some time,

• Station A starts transmitting its 3^rd data packet and station D starts retransmitting its 1^st data packet simultaneously.
• This leads to a collision.

 

At Station A-

 

• The 3^rd data packet of station A undergoes collision for the 1^st time.
• So, collision number for the 3^rd data packet of station A = 1.
• Now, station A randomly chooses a number in the range [0, 2¹-1] = [0,1].
• If station A chooses the number K_A, then back off time = K_A unit.

 

At Station D-

 

• The 1^st data packet of station D undergoes collision for the 3^rd time.
• So, collision number for the 1^st data packet of station D = 3.
• Now, station D randomly chooses a number in the range [0, 2³-1] = [0,7].
• If station D chooses the number K_D, then back off time = K_D unit.

 

Following 16 cases are possible-

 

KA	KD	Remarks
0	0	In this case, both the stations start retransmitting their data immediately. This case leads to a collision again.
0	1	In this case, station A starts retransmitting its data immediately while station D waits for 1 unit of time. This case leads to A successfully retransmitting its data after the 3rd collision.
0	2	In this case, station A starts retransmitting its data immediately while station D waits for 2 unit of time. This case leads to A successfully retransmitting its data after the 3rd collision.
0	3	In this case, station A starts retransmitting its data immediately while station D waits for 3 unit of time. This case leads to A successfully retransmitting its data after the 3rd collision.
0	4	In this case, station A starts retransmitting its data immediately while station D waits for 4 unit of time. This case leads to A successfully retransmitting its data after the 3rd collision.
0	5	In this case, station A starts retransmitting its data immediately while station D waits for 5 unit of time. This case leads to A successfully retransmitting its data after the 3rd collision.
0	6	In this case, station A starts retransmitting its data immediately while station D waits for 6 unit of time. This case leads to A successfully retransmitting its data after the 3rd collision.
0	7	In this case, station A starts retransmitting its data immediately while station D waits for 7 unit of time. This case leads to A successfully retransmitting its data after the 3rd collision.
1	0	In this case, station A waits for 1 unit of time while station D starts retransmitting its data immediately. This case leads to D successfully retransmitting its data after the 3rd collision.
1	1	In this case, both the stations wait for 1 unit of time and then starts retransmitting their data simultaneously. This case leads to a collision again.
1	2	In this case, station A waits for 1 unit of time while station D waits for 2 unit of time. This case leads to A successfully retransmitting its data after the 3rd collision.
1	3	In this case, station A waits for 1 unit of time while station D waits for 3 unit of time. This case leads to A successfully retransmitting its data after the 3rd collision.
1	4	In this case, station A waits for 1 unit of time while station D waits for 4 unit of time. This case leads to A successfully retransmitting its data after the 3rd collision.
1	5	In this case, station A waits for 1 unit of time while station D waits for 5 unit of time. This case leads to A successfully retransmitting its data after the 3rd collision.
1	6	In this case, station A waits for 1 unit of time while station D waits for 6 unit of time. This case leads to A successfully retransmitting its data after the 3rd collision.
1	7	In this case, station A waits for 1 unit of time while station D waits for 7 unit of time. This case leads to A successfully retransmitting its data after the 3rd collision.

 

From here,

• Probability of station A to successfully retransmit its data after the 3^rd collision = 13 / 16
• Probability of station D to successfully retransmit its data after the 3^rd collision = 1 / 16
• Probability of occurrence of collision again after the 3^rd collision = 1 / 16

 

In the similar manner, the procedure continues.

 

Important Notes-

 

Note-01:

 

With each successive collision-

• Back off time increases exponentially.
• Collision probability decreases exponentially.

 

Note-02:

 

Back Off Algorithm is also known as Binary Exponential Back Off Algorithm because-

• It works for only two stations.
• The back off time increases exponentially.
• Collision probability decreases exponentially.

 

Note-03:

 

• One disadvantage of Back Off Algorithm is that it shows capture effect.
• It means if a particular station wins the collision one time, then its probability of winning the successive collisions increases exponentially.

 

To gain better understanding about Back Off Algorithm,

Watch this Video Lecture

 

Next Article- Practice Problems On CSMA / CD & Back Off Algorithm

 

Get more notes and other study material of Computer Networks.

Watch video lectures by visiting our YouTube channel LearnVidFun.